Polynômes irréductibles de degré 4 dans F_2[X]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
par ArtyB » 16 Jan 2016, 12:59
Bonjour,
C'est mon premier exercice de ce genre et je voudrais être sûr de bien avoir compris mon cours.
Lorsque l'on cherche le nombre de polynômes irréductibles de degré n dans
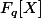
, on utilise la fonction
)
, utilisant la fonction µ de Möbius.
=\frac{1}{n} \sum_d|n µ(d)q^{\frac{n}{d}})
Par exemple pour le nombre de polynômes irréductibles de degré 4 dans
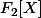
=\frac{1}{4} \sum_d|4 \ \mu(d)2^\frac{4}{d})
Les entiers naturels divisant 4 sont 1 et 2
d'où:
= \frac{1}{4} (\mu(1) \times 2^{\frac{4}{1}} +\mu(2) \times 2^{\frac{4}{2}}))
On a
=1)
et
=-1)
=\frac{1}{4}[1 2^4 -1* 2^2]=\frac{1}{4}(16-4)=3)
Il y a donc 3 polynômes irréductibles de degré 4 dans
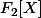
et ceux-ci sont:
,
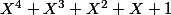
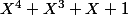
et
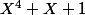
est-ce bien cela ?
Modifié en dernier par
ArtyB le 16 Jan 2016, 13:08, modifié 2 fois.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 16 Jan 2016, 13:01
Moi je compte 8 polynômes de degré 4 à coefficients dans F2, mais toi tu voulais peut-être parler de polynômes irréductibles ?
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
par ArtyB » 16 Jan 2016, 13:07
Ah oui en effet, merci beaucoup, j'ai oublié cette "précision", mea culpa, j'édite de suite.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 16 Jan 2016, 13:13
X4+X3+X+1 est divisible par (X+1) donc n'est pas irréductible.
mais si X4+X+1 est irréductible, alors X4+X3+1 l'est aussi
Et oui normalement tu as 3 polynômes irréductibles.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
par ArtyB » 16 Jan 2016, 13:35
Merci beaucoup de ta réponse !
Encore une erreur de ma part, j'avais bien noté X4+X3+1 sur ma feuille.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
