Polynômes irréductibles dans un corps fini

[wartenberg]

Bonjour,

J'ai vu l'énoncé suivant présenté comme "évident" dans un livre, mais je n'arrive pas à voir pourquoi cela est vrai :

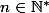
Soit premier, . Il existe un polynôme irréductible de degré dans .
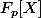
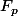
(où désigne le corps à éléments).

Quelqu'un pourrait-il me dire d'où cela provient ?

Merci d'avance !

[jsvdb]

Bonjour wartenberg.
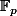
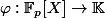
Il suffit de considérer un corps , extension de degré n sur ainsi que le noyau du morphisme qui envoie X sur un générateur du groupe multiplicatif .
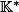
Après, dire que c'est évident, bof bof ...

[wartenberg]

Bonjour jsvdb,

Merci pour ta réponse, mais je ne vois toujours pas comment faire...
De plus, à ce stade (dans le livre), on ne sait pas encore que le groupe multiplicatif des inversibles d'un corps fini est cyclique...

[jsvdb]

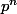
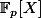
Le soucis, c'est qu'on en a besoin pour voir les corps finis de cardinal comme des quotients de par un polynôme irréductible et montrer ce que tu cherches.
Je ne connais pas autrement.