Exo troublant!!!

[Anonyme]

bonjour
j'ai un petit exo qui m'embarrasse. en fait, je sais resoudre les question mais mais le probleme c'est que ce que j'ai trouvé pour la 1ere question je l'ai refait pour la deuxieme.alors je me demande s'il existe une autre methode pour refaire la premiere??!!
on considere une suite défine par récurrence par Uo>2/3 et U(n+1)=rc(3Un-2) pour n de N.
a) en supposant la suite parfaitement définie:
montrer qu'elle est alors monotone( on precisera la monotonie)
trouver ses limites eventuelles.
b) Prouver que la suite existe et converge dans les cas Uo=1 et Uo=2 et
uo$]1,2[ et uo>2.
c)Montrer qu'au contraire si Uo$]2/3,1[ alors la suite n'est pas définie pour tout n $ N.
j'ai fait la question a et b et c. mais est ce que vous ne trouvez pas que la question a) est la meme que les questions b) et c)????

pour la derniere question
d) Que pensez vous du cas oû Uo=cos(alpha) avec alpha $]0,pi/2[??
ça je l'ai pas fait.
merci inifinment
ah, c'est exo est tiré d'un Td de math...

[Chimerade]

j'ai fait la question a et b et c. mais est ce que vous ne trouvez pas que la question a) est la meme que les questions b) et c)????

Non ! Dans la question a) on suppose la suite parfaitement définie, ce qui te dispense de toute vérification à propos de sa définition, dans les questions b) et c) on te demande au contraire de t'intéresser à la définition, de montrer qu'elle est définie dans tel ou tel cas, et non définie dans tel et tel autre cas.

Si tu as pris la peine de répondre à ces questions en a), alors bien sûr, ce n'est plus la peine de faire b) et c) !

Meilleurs voeux !

[Anonyme]

merci bienchimerade
mais pour la 1ere question ,pour determiner la monotonie j'ai calculé U(n+)-Un
et j'ai trouvé que son signe dépend du signe de -(Un-1)(Un-2) donc on est ramené à distingué les cas Uo>1 Uo>2 Uo$]1,2[ .or cette distincton est dans la 2emme question.
comment faire alors pour préciser la monotonie????

[Chimerade]

merci bienchimerade
mais pour la 1ere question ,pour determiner la monotonie j'ai calculé U(n+)-Un
et j'ai trouvé que son signe dépend du signe de -(Un-1)(Un-2) donc on est ramené à distingué les cas Uo>1 Uo>2 Uo$]1,2[ .or cette distincton est dans la 2emme question.
comment faire alors pour préciser la monotonie????

En fait, on ne peut pas te reprocher d'avoir choisi un chemin différent de celui que te propose l'exercice. Si la définition n'est pas demandée en a), ce n'est pas un péché que d'aborder cette question dès la question a). Si cela te permet de répondre à b) et c) en même temps, ce n'est pas grave. Il est possible que l'auteur du problème ait choisi un autre chemin que toi, qui n'exigeait pas d'entrer dans ces détails pour résoudre a). Si tu juges utile de préciser la définition de la suite pour pouvoir résoudre a), je pense qu'on ne peut pas te le reprocher, sauf si c'est explicitement précisé...

Je pense à des questions comme : "sans calculer la dérivée de f, montrer quelle est croissante !" Dans un cas comme cela, tu es contraint de laisser de côté ta connaissance de la dérivation pour faire un exercice de pur calcul. Mais si l'énoncé ne précise rien de cette manière, tu as tous les droits... Peut-être un professeur de mathématiques de ce forum pourrait te donner un avis plus pertinent...Avis aux volontaires...

Pour info, je n'ai pas essayé de résoudre ton exercice. Je me contente ici de disserter sur des généralités. Mais si tu as réellement besoin d'une solution, je vais alors m'attaquer à ton problème.

@+

[rene38]

Bonjour

a) en supposant la suite parfaitement définie, on peut poser avec et montrer (sans se poser de question d'existence) que est positif d'où est croissante et donc, sous réserve d'existence, est croissante.

[Anonyme]

je vous en remercie
si on prend U(n+1)=f(Un) tel que f(x)=rc(3x-2). pour prouver que Un est croissante il faut s'assurer au préalable que U1>Uo , chose qui me parait compliquée.
alors comment faire pour montrer que U1>Uo??
J'AI VRAIMENT BESOIN DE VOTRE AIDE POUR Résoudre cet exo car FRANCHEMENT JE NE VOIS PAS l'intéret de la question a. autrement dit, je ne réalise pas l'imporatnce de cette phrase " EN supposant la suite ainsi parfaitement définie"
POUVEZ VOUS M'AIDER S'IL VOUS PLAÎT???
MERCI INFINIMENT

[rene38]

je vous en remercie
si on prend U(n+1)=f(Un) tel que f(x)=rc(3x-2). pour prouver que Un est croissante il faut s'assurer au préalable que U1>Uo

Je ne crois pas : on n'a pas affaire à une démonstration par récurrence.
On se contente de dire "f est à dérivée positive donc f est croissante sur son domaine de définition"
On a ainsi démontré que "Si la suite est définie alors elle est monotone croissante"

[Chimerade]

pour prouver que Un est croissante il faut s'assurer au préalable que U1>Uo , chose qui me parait compliquée.
alors comment faire pour montrer que U1>Uo??

Tu as raison : c'est un petit détail qui nous avait échappé.



Il te faut alors constater que cette expression n'est jamais négative, ni nulle. Et pour cela tu dois étudier la fonction , d'où :

calculer g'(x),
constater qu'elle s'annule en ,
en déduire que g décroît de à pour croître ensuite,
et vérifier le minimum de g : qui se trouve être égal à ! Ouf, sauvé ! le minimum de g est positif, donc quel que soit , on aura !

Comme ça, ça devrait aller !

[Anonyme]

ah bon, je ne le savais pas . c'est la premiere fois que je rencontre une telle situation c'est pour cela qu je ne suis pas encore convaincu du fait qu'on n'a pas besoin d'une récurrence pour la premiere question.
pouvez vous détailler u peu votre explication???
mERCI
cordialement

[Chimerade]

Je ne crois pas : on n'a pas affaire à une démonstration par récurrence.
On se contente de dire "f est à dérivée positive donc f est croissante sur son domaine de définition"
On a ainsi démontré que "Si la suite est définie alors elle est monotone croissante"

Je ne suis pas d'accord : barberouss a raison.

Si alors, la croissance de f suffit à montrer que . Mais il faut d'abord montrer que effectivement : la croissance de f ne nous renseigne pas sur le fait que f(x) > x ou pas !

[Anonyme]

je trouve que monsieur Chimerade et rene84 ne sont pas d'accord.
cje suis vraiemrnt embarrassé!!!!

[rene38]

je trouve que monsieur Chimerade et rene84 ne sont pas d'accord.
cje suis vraiemrnt embarrassé!!!!

Tiens, j'ai gagné 46 (84-38) ...
Plus sérieusement, c'est "monsieur Chimerade" qui a raison sur la nécessité de vérifier que U1>U0.
Je maintiens cependant qu'on n'a pas affaire à une démonstration par récurrence.

[Chimerade]

Tiens, j'ai gagné 46 (84-38) ...

!!!!

Je maintiens cependant qu'on n'a pas affaire à une démonstration par récurrence.

Mais si, c'est une récurrence ! La croissance de U n'est pas la conséquence de l'unique croissance de f. Montrer que est une démonstration classique (mais bonne ! Ne pas confondre avec des lessives classiques, qui ne marchent pas !) qui constitue l'amorce de la récurrence.
Pour montrer que , tu as absolument besoin d'avoir montré que et d'utiliser la croissance de f.
Pour moi c'est bel et bien une démonstration par récurrence.

[Chimerade]

Tiens, j'ai gagné 46 (84-38) ...

J'ai compris ! :ptdr: :ptdr: :ptdr:

[Anonyme]

bonjour chimerade
est ce vrai que g decroit de 2/3 à 17/12 mais j'ai trouvé plutot le contraire donc 1/12 est un maximum et là il ya un gros probleme!!!! pouvez vous m'aider???
une autre question :
d) Que pensez vous du cas oû Uo=cos(alpha) avec alpha appartient à ]0,pi/2[???

[Chimerade]

bonjour chimerade
est ce vrai que g decroit de 2/3 à 17/12 mais j'ai trouvé plutot le contraire donc 1/12 est un maximum et là il ya un gros probleme!!!! pouvez vous m'aider???
une autre question :
d) Que pensez vous du cas oû Uo=cos(alpha) avec alpha appartient à ]0,pi/2[???

Oh là là ! Grosse bêtise ! Je suppose que j'avais bu trop de Champagne !

Je suis absolument désolé, j'ai répondu beaucoup trop vite : c'est tout faux !

Comme tu as bien fait d'insister sur la vérification que ! De fait, si et la suite est croissante et tend vers 2, si alors et la suite est décroissante et tend aussi vers 2, si , la suite est constante. Tout cela dépend de g(x) que j'ai mal étudié : effectivement g(x) croît de -2/3 à 1/12 quand x croît de 2/3 à 17/12. Puis il décroît de 1/12 à - l'infini quand x croît de 17/12 à + l'infini. Cela fait que g(x) passe par 0, en 1 et en 2.

Désolé d'avoir bâclé ma réponse : j'en prépare une plus détaillée et plus correcte !

[Anonyme]

merci chimerade, mais je crois que vous avez répondu à la question b) et c) et pas à la question a). car vous avez fait l'étude par cas.(Uo>1 Uo>2....) n'est ce pas???
c'est ça le probleme de cet exo. alors comment faire pour éviter ce désagrément????

[Chimerade]

merci chimerade, mais je crois que vous avez répondu à la question b) et c) et pas à la question a). car vous avez fait l'étude par cas.(Uo>1 Uo>2....) n'est ce pas???
c'est ça le probleme de cet exo. alors comment faire pour éviter ce désagrément????

On en revient au début...

Non, je n'ai pas fini l'étude complète. Pour revenir à la question a), la réponse est bien :
[INDENT]"La suite est monotone parce que la fonction f est croissante, donc, si alors la suite est croissante, si , alors est plus petit que 1 et par conséquent, que la distance de à 2 diminue en gardant le même signe (cette propriété est d'ailleurs conservée : sera également supérieure à 1, c'est facile à démontrer). Cela restreint les valeurs limites candidates à la liste comprenant la seule valeur 2 !

Mais en a), c'est peut-être un peu prématuré...

[Anonyme]

merci encore
une autre question :
que pensez vous du cas oû Uo=cos(alpha) avec alpha $]0,pi/2[ ??
moi je pense que si Uo=cos(alpha) avec alpha $]0,pi/2[ alors la suite ,par recurrence, 0qu'est ce que vous en pensez , c'est juste???

[Chimerade]

Revenons donc à l'étude de g(x) :



La dérivée g'(x) est :



Elle s'annulle en

Elle est bien positive avant cette valeur et négative après, ce qui fait que g croît de 0 à lorsque x croît de 2/3 à 17/12. Puis elle décroit de à 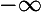lorsque x croît de 17/12 à 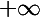. Cela fait qu'elle passe deux fois par zéro. Il est facile de voir que g(1)=g(2)=0 !

Il en résulte, que "tant qu'elle est définie" - et ce point n'a pas encore été abordé - si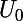 est plus petit que 1 ou plus grand que 2, alors et la suite est croissante et pour , elle est constante. Le graphique joint montre les différentes possibilités.



en b) on dira que la suite est croissante et bornée par 2 si , donc qu'elle est convergente et tend vers 2 (la seule des deux possibilités évoquées dans a)). On dira que la suite est décroissante et bornée par 2 si , donc qu'elle est convergente et tend vers 2 (la seule des deux possibilités évoquées dans a)). Le cas est trivial

enfin, en c) on a déjà dit que la suite était décroissante. Comme elle s'éloigne des deux valeurs candidates 1 et 2 comme limites, on sait qu'elle ne peut être convergente ; cependant il faut préciser si elle est simplement divergente ou si elle n'est même pas définie. Je propose d'utiliser la formule suivante donnée dans mon post précédent :



Elle montre que est strictement plus grand que et même supérieur ou égal à , k étant un nombre strictement plus grand que 1 et qui augmente (c'est mal dit, mais tu me comprends). Il en résulte que la distance de à 2 augmente plus vite qu'une suite géométrique divergente et que nécessairement, on doit arriver à un moment on et qu'à ce moment, ne sera pas défini.

Le cas Uo=cos(alpha) vient dans un autre post...