Exo prepa Henri IV
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Juin 2006, 12:01
par tize » 19 Juin 2006, 12:01
Bonjour à tous,
je planche en ce moment sur un pb de niveau prepa qui à l'air simple (et qui l'est sans doute) voila :
On pose
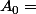
et
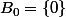
ensuite on définie
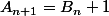
(on ajoute 1 à tous les éléments de Bn) et
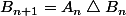
(différence symétrique). Le but est de montrer que
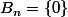
ssi n est une puissance de 2.
Il y a une indication : on pose les polynomes
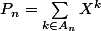
et
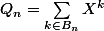
et il faut raisonner modulo 2.
Si vous avez des idées SVP ?
-
mathelot
 par mathelot » 19 Juin 2006, 14:19
par mathelot » 19 Juin 2006, 14:19
avez-vous calculé les premiers termes
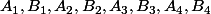
pour vous rendre compte comment ces ensembles d'entiers étaient fabriqués ?
nb: la condition "x n'appartient pas à

" est vraie
-
Bastien
- Messages: 3
- Enregistré le: 10 Juin 2006, 15:50
-
 par Bastien » 19 Juin 2006, 14:28
par Bastien » 19 Juin 2006, 14:28
Tu es sûr de ton énoncé? J'ai peut-être mal compris mais je trouve B2 = {0,1} et B4 = {0,1,2}, et B3 = {0} donc ça paraît mal barré pour montrer le résultat... :hein:
-
mathelot
 par mathelot » 19 Juin 2006, 14:44
par mathelot » 19 Juin 2006, 14:44
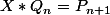
qui se démontre par un changement d'indices (toujours vraie)
si de plus, les polynômes sont à coefficients, non pas dans

mais dans
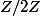
(modulo 2) , on obtient:
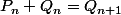
De plus,
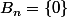
équivaut
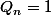
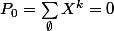
(par définition, une somme prise sur un ensemble d'indices vide vaut zéro).
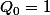
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Juin 2006, 15:38
par tize » 19 Juin 2006, 15:38
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Juin 2006, 15:51
par tize » 19 Juin 2006, 15:51
On aurait donc :
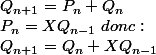
modulo 2.
avec
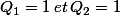
comme condition initiale.
ca ressemble à une suite mod 2 (je chauffe ...)
-
mathelot
 par mathelot » 19 Juin 2006, 15:56
par mathelot » 19 Juin 2006, 15:56
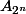
semble être composé de puissances successives de 2.
si on part sur cette base, on pourra calculer le polynôme
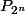
je cherche à voix haute...
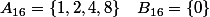
hypothèse de récurrence ??:
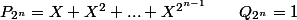
il ne reste plus qu'à se trainer vers
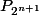
avec nos formules...
^{2}=X^{2}+X^{4}+..+X^{2^{n}}=P_{2^{n+1}}-X)
(les doubles produits sont nuls dans
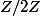
en élevant au carré)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Juin 2006, 20:20
par tize » 19 Juin 2006, 20:20
Bonsoir Mathelot,
quand tu écris
^{2}=X^{2}+X^{4}+..+X^{2^{n}}=P_{2^{n+1 }}-X)
tu l'affirmes parce c'est evident avec nos petites formules ou bien c'est ce que tu veux montrer ?
-
mathelot
 par mathelot » 19 Juin 2006, 20:33
par mathelot » 19 Juin 2006, 20:33
mathelot a écrit:^{2}=X^{2}+X^{4}+..+X^{2^{n}}=P_{2^{n+1}}-X)
(les doubles produits sont nuls dans
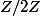
en élevant au carré)
c'est une conséquence de mon hypothèse de récurrence.. A partir de la formule de récurrence, j'élève
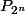
au carré , dans la somme élevée au carré, il y a les doubles produits qui s'en vont car
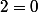
.
^{2}=a^{2}+b^{2}+c^{2}+d^{2})
avec les coeff
dans
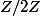
votre exercice est très intéressant. vous publierez la solution ?
-
mathelot
 par mathelot » 19 Juin 2006, 20:42
par mathelot » 19 Juin 2006, 20:42
tize a écrit:On aurait donc :
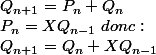
modulo 2.
avec
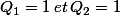
comme condition initiale.
ca ressemble à une suite mod 2 (je chauffe ...)
pourquoi ça ressemble à une suite modulo 2,je ne vois pas...
-
mathelot
 par mathelot » 19 Juin 2006, 21:07
par mathelot » 19 Juin 2006, 21:07
dans mon mail de 16h56, je crois que je me suis emmélé les pinceaux.
je suis sincérement désolé.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Juin 2006, 21:16
par tize » 19 Juin 2006, 21:16
Je dis que c'est une suite "mod 2" car l'égalité :
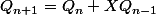
me fait penser à une suite (en l'occurence de polynomes) et "mod 2" car cette égalité est bien sur modulo 2...
Sinon je comprends parfaitement pourquoi :
^{2}=X^{2}+X^{4}+..+X^{2^{n}})
ce que je ne comprends pas c'est pourquoi :
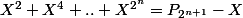
, c'est évident ou c'est à montrer ?
J'ai l'impression que cela sera vrai a partir du moment ou l'on sait que
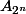
est composé des puissances successives de 2 jusqu'à
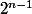
pour tout entier n.
Dites moi si je me trompe.(j'écrirai une solution eu foramt pdf ou dvi par la suite)
-
mathelot
 par mathelot » 19 Juin 2006, 21:26
par mathelot » 19 Juin 2006, 21:26
je suis tout à fait d'accord avec votre dernier post. Par ailleurs,faudrait il établir une formule faisant lien entre la multiplication de 2 polynomes et la différence symétrique ??
-
mathelot
 par mathelot » 19 Juin 2006, 21:41
par mathelot » 19 Juin 2006, 21:41
tize a écrit:ce que je ne comprends pas c'est pourquoi :
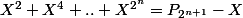
, c'est évident ou c'est à montrer ?
J'ai l'impression que cela sera vrai a partir du moment ou l'on sait que
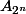
est composé des puissances successives de 2 jusqu'à
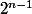
pour tout entier n.
oui, je suis d'accord.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Juin 2006, 21:43
par tize » 19 Juin 2006, 21:43
Peut être...malheureusement je dois aller me coucher je me lève très tôt demain mais je reviens demain avec j'espère de nouvelles idées. A propos d'idée peut que grâce à
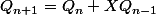
on peut en déduire une relation du genre suite :
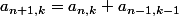
avec
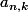
le coefficient d'ordre k associé au polynome Qn sachant que
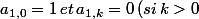\,et\,a_{2,0}=1\,et\,a_{2,k}=0\,(si\,k>0))
...?
Merci beaucoup pour votre aide.(peut etre a demain)
Cordialement.
-
mathelot
 par mathelot » 19 Juin 2006, 22:08
par mathelot » 19 Juin 2006, 22:08
merçi pour votre exercice passionnant.
cordialement.
-
mathelot
 par mathelot » 21 Juin 2006, 21:01
par mathelot » 21 Juin 2006, 21:01
on démontre facilement que
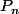
et
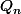
vérifient la même récurrence:

mais pas les mêmes conditions initiales. De plus
mathelot a écrit: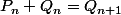
avec cette formule:
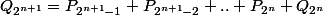
comme on veut montrer l'équivalence:
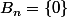
ssi n est une puissance de 2
ça revient à montrer:
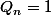
ssi n est une puissance de 2
on est conduit à montrer dans un premier temps:
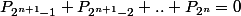
(où la somme comporte
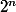
termes).
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Juin 2006, 08:07
par tize » 22 Juin 2006, 08:07
J'en suis arrivé au même point que toi (un peu different quand même):
en me servant de
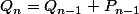
on a:
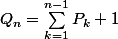
et donc
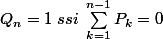
ou même
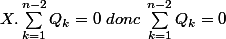
mais ce qui me derange c'est (entre autre le fait que je n'y arrive pas) que même si l'on prouve que l'une des sommes est nulle cela restera modulo 2 et ne prouvera pas que
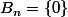
...
-
mathelot
 par mathelot » 22 Juin 2006, 08:49
par mathelot » 22 Juin 2006, 08:49
tize a écrit:si l'on prouve que l'une des sommes est nulle cela restera modulo 2 et ne prouvera pas que
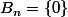
...
je n'ai pas trop de souçis à ce niveau là. Par exemple, l'égalité

implique
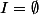
car la famille
_{i \in N})
est libre
dans l'espace vectoriel des polynomes sur le corps de base
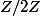
raisonnement: d'habitude, une combinaison linéaire nulle d'une famille libre entraine que les coefficients sont nuls. Or, içi, aucun coefficient n'est nul, c'est donc que l'ensemble d'indices est vide.
-
mathelot
 par mathelot » 22 Juin 2006, 11:15
par mathelot » 22 Juin 2006, 11:15
tize a écrit: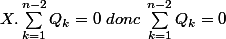
sûr que l'anneau est intègre ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
en élevant au carré)
...