Vieil exo ENS

par **yos** » 11 Déc 2005, 11:48

Soit U(n) une suite bornée à valeurs dans R^p.
On suppose que U(n+1)-U(n) converge vers 0.
Démontrer que l'ensemble de ses valeurs d'adhérences est connexe.

Je sais le faire pour p=1.

Avez-vous des idées pour le cas général.

par **Yipee** » 15 Déc 2005, 07:35

C'est un bel exo. J'ai eu la cas p=1 à traiter en colle quand j'étais étudiant.

J'ai dans l'idée qu'il suffit d'adapter la preuve dans la cas p=1. On note A l'ensemble des valeurs d'adhérences. Soit x un élément de A, on note C sa composante connexe et on suppose par l'absurde qu'il existe un élément y de A qui n'est pas dans C. On remaque alors que C est un compact (fermé borné) et on note d la distance d'un point à C. L'idée est alors de montrer qu'une infinité de fois, on va rentrer et sortir de C en même sortir "assez loin"...

La suite - si nécéssaire - au prochain épisode.

par **Zebulon** » 15 Déc 2005, 08:12

Bonjour,
je suis en licence et je vous crois sur parole (à défaut d'avoir la preuve complète) pour p=1. Pouvez-vous m'expliquer pourquoi on ne peut pas généraliser facilement puisque dans

, un compact est également un fermé borné et qu'une distance de

se généralise dans

en considérant cette distance composante par composante. Peut-être le problème réside-t-il dans le fait que vous utilisez des arguments spécifiques à

dans la démonstration que vous faîtes pour p=1 et dont vous ne donnez que le résultat?
Si c'est le cas, pouvez-vous m'expliquer pourquoi, soit en détaillant la preuve dans

, soit en m'expliquant, par des considérations un peu vagues et non formelles (mais compréhensibles!) où se trouve la difficulté pour généraliser?
Merci.
Zeb.

par **Anonyme** » 15 Déc 2005, 11:43

Ça marche pas en raisonnant simplement coordonnée par coordonnée ?
En dimension 1 on trouve que l'ensemble des valeurs d'adhérence est un segment, en dimension p on devrait trouver un produit de segments, non ?

par **yos** » 15 Déc 2005, 16:48

Je vais regarder vos idées : c'est intéressant.
Ci-dessous l'idée de la preuve dans R . Vous verrez de suite que cela ne s'adapte pas aisément; d'ailleurs dans R on n'a pas besoin que la suite soit bornée. Dans R^p, il faudrait chercher un contre-exemple lorsque la suite n'est pas bornée (s'il y en a!). Autre possible obstacle à la généralisation : dans R connexe=connexe par arc, mais pas dans R^p (p>1).

Soit a < b des valeurs d'adhérence et c compris entre a et b. Il faut montrer que c est valeur d'adhérence aussi. On se donne epsilon>0 et N un entier naturel. Il existe un entier naturel N1 à partir duquel
|U(n+1)-U(n)| On pose M= max(N,N1).
Il existe un indice i>M tel que |U(i)-a|Il existe un indice j>M tel que |U(j)-b|
Parmi les termes de la suite dont les indices sont compris entre i et j, l'un au moins U(k) vérifie |U(k)-c|Cela achève la démonstration.

Je ne crois pas une seconde à l'argument de abcd22 : L'ensemble des valeurs d'adhérence n'a aucune raison d'être un pavé (contre-exemples évidents).

par **Anonyme** » 15 Déc 2005, 17:50

C'est quoi ton contre-exemple évident ?

par **yos** » 15 Déc 2005, 17:58

Une courbe dans le plan d'extrémité A et B et une suite qui va de A à B puis revient de B à A et ainsi de suite indéfiniment en faisant des pas de 1/n.
Tous les points de la courbe sont valeur d'adhérence. Les aller-retours sont en nombre infini car 1+1/2+1/3+...+1/n tend vers +oo.

par **sept-épées** » 15 Déc 2005, 18:01

Je pense que l'hypothèse "bornée" est superflue, et qu'on peut se placer dans n'importe quel espace vectoriel normé (ou espace métrique, en exigeant que d(un+1, un)->0 )

Si E est un espace vectoriel normé, et (un) une suite à valeurs dans E, il est facile de voir que l'ensemble A de ses valeurs d'adhérence est fermé dans E :

si c est un point d'accumulation de A, et si B est une boule centrée en c de rayon r>0, on peut trouver dans la boule de centre c, rayon r/2, un élément a de A, et dans la boule de centre a, rayon r/2, un terme de la suite, qui est alors dans B, ce qui prouve que c est dans A.

Les composantes connexes de A sont alors fermées, et comme la distance entre deux fermés disjoints est strictement positive, vous vous convaincrez vite que A ne peut avoir deux composantes connexes disjointes (sinon on trouverait une suite extraite uf(n) telle que la différence uf(n)+1 - uf(n) reste toujours supérieure à la distance entre ces deux composantes connexes)

QED

par **Anonyme** » 15 Déc 2005, 18:17

Ah oui j'ai écrit trop vite.

par **quinto** » 15 Déc 2005, 23:31

sept-épées a écrit:(Les composantes connexes de A sont alors fermées), et comme la distance entre deux fermés disjoints est strictement positive

Non c'est faux.

par **yos** » 16 Déc 2005, 11:41

Contre-exemple : une courbe et son asymptote!!!

par **yos** » 16 Déc 2005, 13:29

J'ai un autre contre-exemple peut-être plus parlant, suite à la proposition de abcd22. On prend la suite (cos n,sin n) dans R². La suite des abscisses a pour ensemble des valeurs d'adhérence [-1,1] de même que la suite des ordonnées, alors que (cos n,sin n) a pour ensemble des valeurs d'adhérence le cercle de centre O et de rayon 1. Tout ça est connu et assez facile à se représenter. On est donc loin du pavé [-1,1] X[-1,1] .
Ca montre bien qu'on ne peut pas raisonner coordonnée par coordonnée.

Je vous laisse regarder le cas de la suite (cos n, n)

par **sept-épées** » 16 Déc 2005, 20:46

sorry, j'ai déconné.

Mais dans le cadre strict de l'exo, ma démonstration fonctionne : la distance entre deux fermés bornés disjoints de R^n est strictement positive.

Votre contre-exemple montre qu'en effet l'hypothèse "un bornée" est nécessaire : dans R^2, on peut trouver une suite qui a pour valeurs d'adhérence l'axe R+ et la branche d'hyperbole y=1/x pour x>0, et pour laquelle un+1 -un->0. C'est chiant à décrire, mais c'est très-certain.

par **yos** » 16 Déc 2005, 21:12

Peut-être.

1)Si on remplace droite asymptote par cercle asymptote, on a le même problème mais avec des ensembles bornés...en apparence en tout cas.
Je crois que ton argument est viable cependant. Ici on aura fermé+borné donc 2 compacts K et K' et l'application distance de KXK' dans R est continue donc elle atteint ses bornes. Et donc, si les compacts sont disjoints leur distance est >0.

2) Quant au cas non borné, je ne suis pas sûr que ta construction marche. Si ta suite Un se promène tantôt sur l'axe des abscisses, tantôt sur la courbe y=1/x, tout en vérifiant Un+1-Un --->0, peut-être que les points du plan situés entre les deux seraient parfois des valeurs d'adhérence, ce qui pourrait connecter l'adhérence de la suite.

A méditer.

Le cas de l'exo semble réglé.

Merci de l'intérêt que vous y avez porté.

par **sept-épées** » 17 Déc 2005, 13:46

yos a écrit:
1)Si on remplace droite asymptote par cercle asymptote, on a le même problème mais avec des ensembles bornés...en apparence en tout cas.
.

imaginons une spirale qui se rapproche du cercle, du style la courbe polaire r=1+1/t . Elle n'est pas fermée dans R^2, il faut lui ajouter les points du cercle...

yos a écrit:2) Quant au cas non borné, je ne suis pas sûr que ta construction marche. Si ta suite Un se promène tantôt sur l'axe des abscisses, tantôt sur la courbe y=1/x, tout en vérifiant Un+1-Un --->0, peut-être que les points du plan situés entre les deux seraient parfois des valeurs d'adhérence, ce qui pourrait connecter l'adhérence de la suite.

En effet, c'est assez pénible à décrire, mais je pense que ça marche : vous savez construire une suite un qui a tous les points de la droite R comme valeurs d'adhérence, et une autre vn qui a tous les points de la branche d'hyperbole comme valeurs d'adhérence. Il suffit alors de les emboîter l'une dans l'autre (c'est à dire de définir une suite en prenant alternativement un certain nombre de termes de un, puis un certain nombre de termes de vn etc.), la seule contrainte étant que la distance entre deux termes consécutifs doit tendre vers 0, contrainte qui peut être satisfaite puisque les deux courbes sont asymptotes. L'ensemble des valeurs d'adhérence de cette suite est alors exactement la réunion des deux courbes.

par **quinto** » 17 Déc 2005, 14:32

sept-épées a écrit:sorry, j'ai déconné.

Mais dans le cadre strict de l'exo, ma démonstration fonctionne : la distance entre deux fermés bornés disjoints de R^n est strictement positive.

Ca c'est vrai en revanche.
On peut même supprimer une hypothèse:
1 fermé et un compact disjoint sont à une distance strictement positive.

par **Joker62** » 04 Déc 2007, 18:36

Bonsoir ;)
J'regardais les posts de l'ami Yos et j'suis tombé ici :)
J'voulais juste avoir un complément sur cet exo :

Comme l'a précisé Yos, c'est pas très clair le fait qu'il y ait entre les indices i et j, des termes de la suite très proches de c.

Donc dans R, quel est l'argument pour conclure ??? :o
Merci ;)

par **ThSQ** » 04 Déc 2007, 20:52

Intéressant comme exo !

Dans IR^2 je pense avoir un contrex.

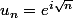parcourt le cercle de moins en moins vite :

Bon les valeurs d'adhérence c'est tout le cercle unité donc connexe. Mon idée est de faire traverser la suite en ligne droite en passant par (0,0) tous les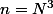

par exemple (i.e rarement pour pas risquer de faire des tas ou de ne plus être dense dans le cercle) pas de

. Après avoir traversé on repart dans le même sens.

Intuitivement le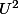

et (0,0) sont les valeurs d'adhérence et c'est pas connexe.

par **yos** » 04 Déc 2007, 23:45

Je vois qu'on remue les vieilles histoires. Cherche pas de contrex, c'est juste. Je t'écrirai la preuve un jour.

par **Joker62** » 05 Déc 2007, 00:35

Ouai trés vieux !
Mais on est d'accord que c'est aussi trés bon...

sinon pour ma part, l'explication de la preuve pour p=1 me suffirait. Enfin si y'a le cas général pourquoi pas. Merci bien

Vieil exo ENS

Vieil exo ENS

vrai dans n'importe quel espace vectoriel normé

excuses

Qui est en ligne