Exo prepa Henri IV
41 messages
- Page 2 sur 3 - 1, 2, 3
mathelot a écrit:je n'ai pas trop de souçis à ce niveau là. Par exemple, l'égalitéimplique
car la famille
est libre
dans l'espace vectoriel des polynomes sur le corps de base
raisonnement: d'habitude, une combinaison linéaire nulle d'une famille libre entraine que les coefficients sont nuls. Or, içi, aucun coefficient n'est nul, c'est donc que l'ensemble d'indices est vide.
Compris, tout a fait d'accord
Bonsoir Mathelot.
Je viens de rentrer du boulo je peux donc enfin reflechir un peu sur mon problème.
Je suis revenu à la relation de recurrence :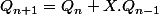 et je me suis dis (tant pis si c'est ca ne tient pas debout, je verrai à la fin) que je peux très bien etudier cette suite et essayer de l'expliciter : pour cela il suffit de résoudre l'équation :
et je me suis dis (tant pis si c'est ca ne tient pas debout, je verrai à la fin) que je peux très bien etudier cette suite et essayer de l'expliciter : pour cela il suffit de résoudre l'équation :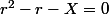 dont les solutions sont :
dont les solutions sont : }{2}\;et\;r_2=\frac{1-\sqrt(1+4X)}{2}) (je sais que
(je sais que  ne veut pas dire grand chose mais apres dans la formule ils devraient s'annuler).
ne veut pas dire grand chose mais apres dans la formule ils devraient s'annuler).
On trouve après quelques calculs et en posant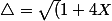) :
:
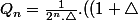^n-(1-\triangle)^n))
Je ne pense pas m'être trompé (mais je n'ai vérifier pour l'instant que pour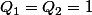 )
)
Je viens de rentrer du boulo je peux donc enfin reflechir un peu sur mon problème.
Je suis revenu à la relation de recurrence :
On trouve après quelques calculs et en posant
Je ne pense pas m'être trompé (mais je n'ai vérifier pour l'instant que pour
mathelot a écrit:il est impossible de diviser par 2 dans!
oui c'est vrai... mais en faite quand on developpe cette formule (formelle), on peut très bien considérer que la relation de recurrence n'est plus dans
les
Enfin ...je dis aussi peut être n'importe quoi.
Tenez moi au courant si votre methode donne des fruits.
Merci
Ce que je veux dire (je me suis un peu enbrouillé les pinceaux dans mon message precedent) c'est que l'on peu considérer la suite de polynome (qui n'est pas dans  :\;Q'_n) avec
avec 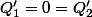 et definie par la recurrence :
et definie par la recurrence : 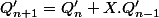 avec celle-ci, il n'y a pas de problème pour ma methode et en plus lorsque (pour n donné) on transforme les coefficients de
avec celle-ci, il n'y a pas de problème pour ma methode et en plus lorsque (pour n donné) on transforme les coefficients de  en regardant ceux-ci modulo 2 on trouve justement
en regardant ceux-ci modulo 2 on trouve justement 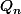
(déja démontré) a écrit:
notation:j'écris un vecteur colonne sous la forme
En mettant les relations en matrice, et avec ma notation:
où A est la matrice:
A a pour polynome caractéristique ton polynome:
ce polynôme n'est pas scindé sur
conduit au système
qui n'a pas de solution dans
conclusion: la matrice A n'est pas diagonalisable et il va falloir trouver
sa puissance n-ième "à la main". Faut il étudier les combinaisons
Avec ma methode : 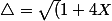 :) on a :
on a : 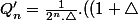^n-(1-\triangle)^n)) et
et 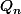 est égal à 1 ssi
est égal à 1 ssi  est un polynome dont tous les coefficients sont pairs sauf le terme constant. En développant
est un polynome dont tous les coefficients sont pairs sauf le terme constant. En développant  on trouve :
on trouve : 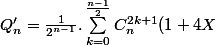^k$$) si n est impair et
si n est impair et
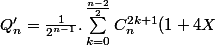^k$$) si n est pair
si n est pair
On a alors le coefficient de degré p du polynome :
:
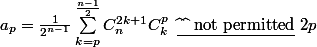 si n est impair.
si n est impair.
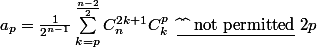 sinon
sinon
la question est maintenant pour quelles valeurs de a-t-on
a-t-on 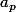 est pair pour tout
est pair pour tout  >0 ?
>0 ?
Concernant ta methode, je trouve qu'elle est très bien et a mon avis on pourrait même diagonaliser ta matrice a condition d'utiliser la même astuce : poser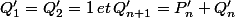 le tout etant dans
le tout etant dans  par exemple. Là il n'y aura pas de problème pour diagonaliser ta matrice et on s'en sort avec le fait que le morphisme
par exemple. Là il n'y aura pas de problème pour diagonaliser ta matrice et on s'en sort avec le fait que le morphisme  de
de  qui transforme les coefficients en donnant leur classe modulo 2 transforme
qui transforme les coefficients en donnant leur classe modulo 2 transforme =Q_n) .
.
On a alors le coefficient de degré p du polynome
la question est maintenant pour quelles valeurs de
Concernant ta methode, je trouve qu'elle est très bien et a mon avis on pourrait même diagonaliser ta matrice a condition d'utiliser la même astuce : poser
J'ai trouvé !!!!
C'est un bel exercice. J'ai trouvé la solution à l'instant. La méthode consiste à trouver une relation entre  et
et 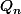 . Pour cela on pose
. Pour cela on pose 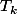 et
et 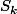 des polynômes tels que
des polynômes tels que

Je vous laisse vérifier les propriétés que vérifient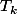 et
et 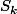 et conclure...
et conclure...
Je vous laisse vérifier les propriétés que vérifient
On pose  et
et  et on raisonne modulo 2.
et on raisonne modulo 2.
On trouve :
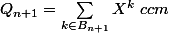
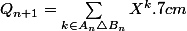
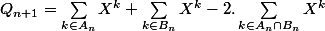
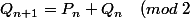\quad (*)\hspace{1cm}$$)
et :
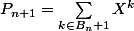
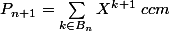
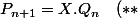\hspace{2.8cm}$$)
On en déduit, grâce à$) et
et $) les relations :
les relations :
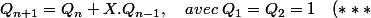$$)

On cherche ensuite pour tout entier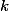 des polynômes
des polynômes  et
et  tels que :
tels que :
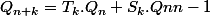
Pour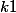 , on a
, on a 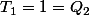 et
et 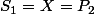 et ensuite on en déduit grâce à
et ensuite on en déduit grâce à $) que
que  et
et  doivent vérifier :
doivent vérifier :
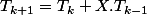 et
et 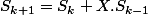 et
et
avec les conditions initiales on a :
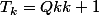 et
et 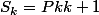 .
.
Donc :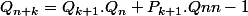 ou encore avec
ou encore avec 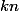 :
:
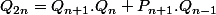 et grâce à
et grâce à $) et
et $) :
: 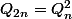 et pour finir :
et pour finir : 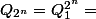
Un très grand merci à Yipee pour la proposition de solution et à Mathelot pour sa participation très active.
On trouve :
et :
On en déduit, grâce à
On cherche ensuite pour tout entier
Pour
avec les conditions initiales on a :
Donc :
Un très grand merci à Yipee pour la proposition de solution et à Mathelot pour sa participation très active.
Je reviens sur ce probleme. Je n'ai pas reussi à aboutir avec mon étude de suite mais je suis tombé par hasard cette semaine sur un oral de polytech qui correspond au probleme et eux donne une solution en etudiant la suite:
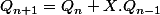 d'équation caractéristique
d'équation caractéristique  qui n'a pas de solution dans
qui n'a pas de solution dans  mais qui en a dans un sur corps, on note les solutions :
mais qui en a dans un sur corps, on note les solutions :  et
et  . On aurait alors avec les conditions
. On aurait alors avec les conditions
initiales et en posant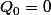 pour que la suite soit indexée dans
pour que la suite soit indexée dans  ,
, 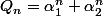 . D'autre part
. D'autre part 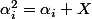 et
et 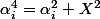 (car dans
(car dans  les doubles produits sont nuls). On montre alors très facilement par récurrence que
les doubles produits sont nuls). On montre alors très facilement par récurrence que 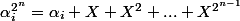 et donc
et donc
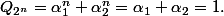
(On remarquera qu'on ne montre pas la reciproque avec cette methode)
initiales et en posant
(On remarquera qu'on ne montre pas la reciproque avec cette methode)
41 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
