Exo prepa Henri IV

[tize]

Je reviens sur ce probleme. Je n'ai pas reussi à aboutir avec mon étude de suite mais je suis tombé par hasard cette semaine sur un oral de polytech qui correspond au probleme et eux donne une solution en etudiant la suite:
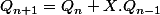
d'équation caractéristique qui n'a pas de solution dans mais qui en a dans un sur corps, on note les solutions : et . On aurait alors avec les conditions
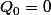
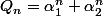
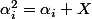
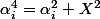
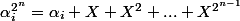
initiales et en posant pour que la suite soit indexée dans , . D'autre part et (car dans les doubles produits sont nuls). On montre alors très facilement par récurrence que et donc

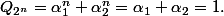
(On remarquera qu'on ne montre pas la reciproque avec cette methode)