Exercice de td

[maths62]

Bonjour
Pouvais vous m'aider à comprendre la question 1 s'il vous plait ?
f: [a,b] C une fonction (R)-intégrable

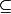
1 On suppose que f est continue et qu'il existe un point t0 [a,b] tel f(t0) 0. Montre qu'il existe un intervalle non trivial [ , ] [a,b] et une constante >0 tel que |f(t)| pour tout t [ ,]

2) On suppose f continue . Montrer que si =0, alors f=0


3) Montre que ce qu'on obtient à la 2 est faux si f n'est pas continu

[aviateur]

Là tu insistes en posant la même question partout.

Mais c'est à toi de travailler:
Commence par écrire la définition (correcte) de f continue en t_0. Sans cela on ne peut rien faire.