P(X²)=P(X)P(X-1) // exercice polynome
34 messages
- Page 1 sur 2 - 1, 2
P(X²)=P(X)P(X-1) // exercice polynome
Bonjour, un exercice me pose quelques difficultés
on me donne ceci: sot P un polynome à coeff. réels, non constant, tel que: P(X²)=P(X)P(X-1)
la question "introductive" est "qu'est ce qui permet d'affirmer que P admet au moins une racine complexe?"
J'ai pensé au théorème d'Alembert Gauss qui dit "tout polynome non constant de C[X] admet au moins une racine dans C"
le soucis c'est que ce théorème n'est valable que dans C, on a bien écrit dans le cours qu'il n''est pas vrai dans R mais ne peut-on pas dire malgré tout "tout polynome non constant de R[X] admet au moins une racine dans C"?
Je suis certaine que c'est ce théorème qu'il faut citer mais l'expliquer me semble d'un coup plus complexe
merci d'avance
on me donne ceci: sot P un polynome à coeff. réels, non constant, tel que: P(X²)=P(X)P(X-1)
la question "introductive" est "qu'est ce qui permet d'affirmer que P admet au moins une racine complexe?"
J'ai pensé au théorème d'Alembert Gauss qui dit "tout polynome non constant de C[X] admet au moins une racine dans C"
le soucis c'est que ce théorème n'est valable que dans C, on a bien écrit dans le cours qu'il n''est pas vrai dans R mais ne peut-on pas dire malgré tout "tout polynome non constant de R[X] admet au moins une racine dans C"?
Je suis certaine que c'est ce théorème qu'il faut citer mais l'expliquer me semble d'un coup plus complexe
merci d'avance
Très bien donc je dis que P est un poly à coeff dans R donc dans C (R contenu dans C) et comme P est non constant d apres le theoreme d'Al-Gauss, P admet au moins une racine complexe.
Merci, je crois qu'avoir écrit "ce théorème est faux dans R" m'a fait bloquée betement :hum:
Dans les questions suivantes on veut montrer que 0 ne peut être racine de P en raisonnant par l'absurde en supposant P(0)=0
on considere une suite (un), pour tout n de N, définie par u0=0 et la relation de récurrence:
^{2})
1/ démontrer que pour tout n de N, P(un) =0
j'ai commencé mon raisonnement par récurrence mais je bloque à l'hérédité (décidemment):
pour tout n de N, on pose Pn la propriété suivante: P(un) =0
initialisation: on vérifie Po: u0=0 d'apres l énoncé, donc P(u0)=P(0)
or P(0) =0 par hypothèse donc P(u0)=0
Po est vérifiée
Hérédité: on suppose Pn vraie à partir d un certain rang n fixé. On montre Pn+1: "P(un+1)=0"
en partant de l'expression du polynome:
P(Un²)=P(Un)*P(Un - 1)
comme P(Un)=0 par Hypothese de récurrence P(Un²) =0 mais ça me sert pas ...comment faire?!
Merci, je crois qu'avoir écrit "ce théorème est faux dans R" m'a fait bloquée betement :hum:
Dans les questions suivantes on veut montrer que 0 ne peut être racine de P en raisonnant par l'absurde en supposant P(0)=0
on considere une suite (un), pour tout n de N, définie par u0=0 et la relation de récurrence:
1/ démontrer que pour tout n de N, P(un) =0
j'ai commencé mon raisonnement par récurrence mais je bloque à l'hérédité (décidemment):
pour tout n de N, on pose Pn la propriété suivante: P(un) =0
initialisation: on vérifie Po: u0=0 d'apres l énoncé, donc P(u0)=P(0)
or P(0) =0 par hypothèse donc P(u0)=0
Po est vérifiée
Hérédité: on suppose Pn vraie à partir d un certain rang n fixé. On montre Pn+1: "P(un+1)=0"
en partant de l'expression du polynome:
P(Un²)=P(Un)*P(Un - 1)
comme P(Un)=0 par Hypothese de récurrence P(Un²) =0 mais ça me sert pas ...comment faire?!
C'est très clair j'ai repris chaque étape de l'égalité et j'ai saisi, merci!
Ensuite j'ai du montrer que pour tout n de N,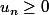
et que la suite (un) était strictement croissante. Ce que j'ai fait.
La question qui termine cette partie de l'exo est "en déduire que P est le polynome nul". J'ai rédigé ainsi:
comme P(Un) =0 et que Un est croissante strictement alors P ne varie pas en fonction de X et reste constant et égal à 0: c'est donc le polynome nul qui ne dépend pas de x...
est-ce correct?
Ensuite j'ai du montrer que pour tout n de N,
et que la suite (un) était strictement croissante. Ce que j'ai fait.
La question qui termine cette partie de l'exo est "en déduire que P est le polynome nul". J'ai rédigé ainsi:
comme P(Un) =0 et que Un est croissante strictement alors P ne varie pas en fonction de X et reste constant et égal à 0: c'est donc le polynome nul qui ne dépend pas de x...
est-ce correct?
Non, ce que tu as écrit n'a pas vraiment de sens.
Tu as montré que U(n) est strictement croissante, ce qui veut dire qu'en particulier tous les U(n) sont différents et en nombre infini. Et comme chaque u(n) est une racine de P, cela veut donc dire que P admet une infinité de racines distinctes ! Conclusion?
Tu as montré que U(n) est strictement croissante, ce qui veut dire qu'en particulier tous les U(n) sont différents et en nombre infini. Et comme chaque u(n) est une racine de P, cela veut donc dire que P admet une infinité de racines distinctes ! Conclusion?
on peut dire alors que le degré du polynome est infini ce qui correspond au polynome nul! merci !
désolée de vous déranger encore , dans la 2eme partie on me demande: "on veut démontrer dans la suite que toutes les racines complexes de P sont necessairempent de module 1. on entame un nouveau raisonnement en supposant l'existance d'une racine a appartenant à C* de P telle que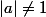
démontrer que pour tout n de N, P(a^2n)=0
je ne sais pas du tout comment partir, dois je me servir du fait que p(un) =0 de la premiere partie?
désolée de vous déranger encore , dans la 2eme partie on me demande: "on veut démontrer dans la suite que toutes les racines complexes de P sont necessairempent de module 1. on entame un nouveau raisonnement en supposant l'existance d'une racine a appartenant à C* de P telle que
démontrer que pour tout n de N, P(a^2n)=0
je ne sais pas du tout comment partir, dois je me servir du fait que p(un) =0 de la premiere partie?
Je saisis parfaitement ce que vous voulez dire puisqu'un nombre complexe élevé à la puissance 2^n voit son module élevé cette même puissance et son argument est multiplié par 2^n (à 2pi près)
La question suivante "en déduire que P est le polynome nul et conclure"
On a montré que pour tout n de P=0)
et on a ainsi justifié que les termes de la suite étaient distincts car le module différait.
C'est parce que de nouveau la suite est croissante et qu'il y a une infinité de solution que P est nécessairement le polynome nul?
Merci
La question suivante "en déduire que P est le polynome nul et conclure"
On a montré que pour tout n de P
et on a ainsi justifié que les termes de la suite étaient distincts car le module différait.
C'est parce que de nouveau la suite est croissante et qu'il y a une infinité de solution que P est nécessairement le polynome nul?
Merci
Ok très bien, merci; et en terme de conclusion je peux dire:
"or il y a contradiction! P n'est pas constant donc P ne peut être le polynome nul. Autrement dit il n'existe pas de racine a de C* de P telle que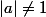 " achevant ainsi le raisonnement par l'absurde de cette 2ème partie.
" achevant ainsi le raisonnement par l'absurde de cette 2ème partie.
Et enfin la dernière partie de l'exercice on me dit "soit a une racine de P et A le point du plan complexe d'affixe a"
on m'a demandée quelle info géométrique sur la position de A je pouvais tirer de la question précédente (P est le polynome nul et la conclusion). J'ai dit que si a est racine du polynome et que son module vaut toujours 1 alors A se situe sur le cercle trigo.
Ensuite on me demande de montrer que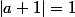 et d'en déduire géométriquement une autre info sur A.
et d'en déduire géométriquement une autre info sur A.
Je sèche un peu là, comment démarrer pour cette question? J'ai pensé écrire a comme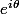 avec théta dans R mais bon ça ne m'avance guère...
avec théta dans R mais bon ça ne m'avance guère...
"or il y a contradiction! P n'est pas constant donc P ne peut être le polynome nul. Autrement dit il n'existe pas de racine a de C* de P telle que
Et enfin la dernière partie de l'exercice on me dit "soit a une racine de P et A le point du plan complexe d'affixe a"
on m'a demandée quelle info géométrique sur la position de A je pouvais tirer de la question précédente (P est le polynome nul et la conclusion). J'ai dit que si a est racine du polynome et que son module vaut toujours 1 alors A se situe sur le cercle trigo.
Ensuite on me demande de montrer que
Je sèche un peu là, comment démarrer pour cette question? J'ai pensé écrire a comme
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
