bonjour.
quelques unes pour la route.
u_n= (1/2+1/2n)^n on me dit comparer avec une série géométrique.
A première vu le critère de la racine semble marcher (si |un|^1/n)<r avec 0

r <1 alors la série converge absolument), pour n

2, |un|

3/4 <1 ok. en fait ça "revient au même" de dire que q^n <= (3/4)^n puis comme 3/4 <1
)
est majorée par une série géometrique convergente .
le genre de série où je galère (toujours comparer à une série géometrique):
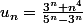
en fait je me souviens d'un petit exo que j'ai pas réussi à résoudre ie chercher à majorer a^x/x^n (ou son inverse je sais plus) et je me dis que c'est potentiellement une lacune qui m'empêche de proner que la série des u_n converge.
une dernière: un= 1 - cos(1/n), on fait un dl de cos en 0 à mon avis, on a cos(1/n)= 1-(1/n)²/2+ (1/n)^4)/4! +o(truc)= 1 - 1/2n²+ 1/(n^4*4!)+o(truc) donc que un= 1/2n²-1/n^4*4! +o(truc)
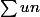
est donc somme de 2 séries de riemann convergentes cqfd! on pourrait même faire un dl à un seul terme non
le tex c'est horrible au fait, plus lisible pour les autres mais très chiant




