2719 résultats trouvés
Revenir à la recherche avancée
ça m'interesse. J'ai jamais fait ça. As tu une bonne référence pour la résolution d'équation diophantienne ? pour ton pb, a priori, pas de solution: y=-2x+25/3 On se débarassera jamais du tiers avec des entiers Oui, si on considére qu'un prix est un nombre entier. Soit un couple (x,y) tel q...
- par Clembou
- 04 Aoû 2006, 11:45
-
- Forum: ✎✎ Lycée
- Sujet: Une équation à deux inconnues
- Réponses: 4
- Vues: 837
Je ne sais pas où placé cet exercice mais je suis sûr que des lycéens qui s'intéressent aux mathématiciens pourraient résoudre ce problème. Le voici : Hier, j'ai acheté six disques et trois crayons chez un marchand. Est-ce possible de calculer le prix d'un disque et d'un crayon sachant que ma dépens...
- par Clembou
- 04 Aoû 2006, 11:13
-
- Forum: ✎✎ Lycée
- Sujet: Une équation à deux inconnues
- Réponses: 4
- Vues: 837
Voici un exercice intéressant pour les collégiens dont voici l'énoncé. Données de la figure : Tracer un triangle ABC rectange en B avec AB=4 cm et BC=2 cm, un rectangle BEDC avec BE=4 cm, un triangle CDF rectangle en D avec DF = 4 cm, le demi-cercle (AF) Laire de la partie rouge est la somme des ai...
- par Clembou
- 04 Aoû 2006, 10:50
-
- Forum: ✎ Collège et Primaire
- Sujet: Calcul d'aire d'une figure composé
- Réponses: 5
- Vues: 5023
Tu as déjà posé cette question dans un autre post

Bon, moi, j'ai trouvé que la primitive de
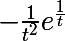
est égale à
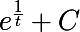
Peut-être que ça pourrait t'aider
Edit : Ok ! Je ne l'avais pas vu cette petite faute de frappe. Merci nox
- par Clembou
- 04 Aoû 2006, 10:24
-
- Forum: ⚜ Salon Mathématique
- Sujet: une primitive?
- Réponses: 13
- Vues: 1220
Oui mais quand on n'a pas de solution évidente, il faut utiliser des formules comme celle de Cardan-Tartaglia pour la résolution des équations du troisième degré.
- par Clembou
- 04 Aoû 2006, 10:00
-
- Forum: ⚜ Salon Mathématique
- Sujet: résolution d'équation
- Réponses: 10
- Vues: 1378
Bonjour a tous , dans un exercice de travail de vaccances j'ai un probleme , il nous demande de prouver que la suite est geometrique facile me dirait vous mais non ^^ , il faut faire Un +1 / un mais regardais la suite Un = (n + 1 / 3n ) a la puissance n . Voila j'ai fait plein de brouillon mais c'e...
- par Clembou
- 04 Aoû 2006, 09:55
-
- Forum: ✎✎ Lycée
- Sujet: les suites geometriques XD
- Réponses: 8
- Vues: 603
Ce n'est sûrement pas du niveau de collège mais on peut facilement trouver en remplaçant x par des petites valeurs.
- par Clembou
- 04 Aoû 2006, 09:52
-
- Forum: ✎✎ Lycée
- Sujet: equation
- Réponses: 17
- Vues: 1104
Cela dépend dans quel intervalle tu veux la calculer. Bon, là, je prend un intervalle [x,y] , tu remplaceras par les valeurs voulues (attention x\neq 0 et y\neq 0 sinon on ne peut pas calculer la primitive). Une derivée de e^u (sachant que u est une fonction) c'est u' \times e^u . Recherchons u'...
- par Clembou
- 04 Aoû 2006, 09:48
-
- Forum: ✯✎ Supérieur
- Sujet: Integrale simple
- Réponses: 21
- Vues: 1736
Au lycée (en France) on ne voit pas la notion de bijection, ni les déterminants. Donc on ferait comme j'ai proposé dans mon premier post, c'est-à-dire chercher les solutions de x et y en fonction de X et Y. Si on arrive à exprimer x et y, alors on peut dire que c'est une bijection. Avec les détermi...
- par Clembou
- 04 Aoû 2006, 08:56
-
- Forum: ✎✎ Lycée
- Sujet: application bijective
- Réponses: 22
- Vues: 2280
Moi, je rentre en L1 pour une license Math à Lille 1. Je pense que l'année prochaine, on sera dans la même université lol :lol:
- par Clembou
- 04 Aoû 2006, 08:49
-
- Forum: ✎ Collège et Primaire
- Sujet: Sans calculette ^^
- Réponses: 27
- Vues: 2592
Ok ! :) Ca fait plaisir qu'il n'y a pas que moi qui veut faire professeur de maths (parce que quand on dit : j'ai envie de faire prof de maths à des jeunes aujourd'hui, c'est pas très commun :lol:). Tu étudies où ?
- par Clembou
- 03 Aoû 2006, 22:01
-
- Forum: ✎ Collège et Primaire
- Sujet: Sans calculette ^^
- Réponses: 27
- Vues: 2592
raptor77 a écrit:Moi a part commencer à réviser je fais rien :zen:
Commencer à réviser ? C'est pas les deux dernières semaines d'août qui faut faire ça ? lol

Hé bien, si tu as rien à faire, révises

Moi pendant ce temps là, je faisais un site de mathématiques mais j'ai arrêté faute de motivation...
- par Clembou
- 03 Aoû 2006, 21:59
-
- Forum: ⚑ À propos de ce site
- Sujet: ah les vacances
- Réponses: 13
- Vues: 1681
On est jeudi soir et voilà que la semaine prochaine je m'en vais dans un camping vide pendant trois semaines avec mes grands parents. Les vacances, c'est juste pour faire chier tout le monde lol :lol:
- par Clembou
- 03 Aoû 2006, 21:45
-
- Forum: ⚑ À propos de ce site
- Sujet: ah les vacances
- Réponses: 13
- Vues: 1681
Merci à toi nekros de m'accueillir... Pour une courte présentation, venez voir mon profil. Je suis sur ce forum pour aider principalement les collégiens en difficulté (prof de maths au collège dans 5 ans si tout va bien). Donc voilà !
- par Clembou
- 03 Aoû 2006, 21:42
-
- Forum: ✎ Collège et Primaire
- Sujet: Sans calculette ^^
- Réponses: 27
- Vues: 2592
Bonjour à tous,
il serait plus convenable d'écrire avec les balises [tex], les calculs mathématiques. Parce que là entre symboles de puissances, de fractions, de racine carrée, ça embrouille :)
Désolé d'être casse-c**** pour mes premiers messages mais bon... :)
- par Clembou
- 03 Aoû 2006, 21:14
-
- Forum: ✎ Collège et Primaire
- Sujet: Sans calculette ^^
- Réponses: 27
- Vues: 2592
Problème assez difficile... lol :lol: La fonction n'est pas définie quand x=0 car 0^0 n'existe pas. En prenant x=-1, on peut trovuer que y=2 En prenant x=1, on peut trouver que y=4 On peut alors dire que l'équation suivante ne possède aucune solution car si on prend une valeur proche de 0 tel que la...
- par Clembou
- 03 Aoû 2006, 21:11
-
- Forum: ✎✎ Lycée
- Sujet: equation
- Réponses: 17
- Vues: 1104