52 résultats trouvés
Revenir à la recherche avancée
Ecrire matriciellement
Salut, tout le monde avant de poser ma question, Je commence par cette notion en geometrie projective: la transformation \hat{x} = \frac{fx}{z} \hat{y} = \frac{fy}{z} \hat{z} = f peut s'ecrire sous forme matricielle, comme suit; \begin{pmatrix} s \hat{x}\\ s \hat{y}\\ s \hat{z} \\ s \end{pmatrix}= \...
- 02 Mar 2021, 22:50
- Forum: ✯✎ Supérieur
- Sujet: Ecrire matriciellement
- Réponses: 0
- Vues: 279
Algébriser
Salut, tout le monde avant de poser ma question, Je commence par cette notion en geometrie projective: la transformation \hat{x} = \frac{fx}{z} \hat{y} = \frac{fy}{z} \hat{z} = f peut s'ecrire sous forme matricielle, comme suit; \begin{pmatrix} s \hat{x}\\ s \hat{y}\\ s \hat{z} \\ s \end{pmatrix}= \...
- 02 Mar 2021, 22:49
- Forum: ⚔ Défis et énigmes
- Sujet: Algébriser
- Réponses: 0
- Vues: 337
- 01 Nov 2018, 20:54
- Forum: ✯✎ Supérieur
- Sujet: Demonstration du théoreme de Godunov
- Réponses: 1
- Vues: 291
Demonstration du théoreme de Godunov
Bonjour , je Cherche des idée pour la demonstration de ce theoreme dit de Godunov Soit X un espace vectoriel normé tel que pour tout f:I \times X \rightarrow X continue , et pour tout x_0 \in X le probleme de Cauchy : \left\lbrace\begin{matrix} x'&=f(t,x(t)) \\ x(t_0)...
- 24 Oct 2018, 10:37
- Forum: ✯✎ Supérieur
- Sujet: Demonstration du théoreme de Godunov
- Réponses: 1
- Vues: 291
Re: Suite de Cauchy
Salut
la question est mal ecrit que voulais tu dire par Si $x_{2}$ ...
la question est mal ecrit que voulais tu dire par Si $x_{2}$ ...
- 09 Juin 2018, 01:33
- Forum: ✯✎ Supérieur
- Sujet: Suite de Cauchy
- Réponses: 13
- Vues: 748
EVT non localement convexe
Bonjour Notons l^{\frac{1}{2}}=\{ x=(x_n)_{n\in \N } \in \R^{\N} : \sum_{n=0}^{+\infty}{\sqrt{\left|x_n \right|}}<+\infty \} et d(x,y)=\sum_{n=0}^{+\infty}{\sqrt{\left|x_n - y_n \right|}} 1) Montrer que d est une distance sur l^{\frac{1}{2}} (en particulier d est finie ) 2) soit \tau...
- 08 Juin 2018, 22:35
- Forum: ✯✎ Supérieur
- Sujet: EVT non localement convexe
- Réponses: 1
- Vues: 358
Re: Analyse fonctionnelle
non ceci est évident mon problème est avec la somme infinie
- 08 Juin 2018, 20:55
- Forum: ✯✎ Supérieur
- Sujet: Analyse fonctionnelle
- Réponses: 8
- Vues: 475
Re: Analyse fonctionnelle
pardon je voulais dire si la série converge vers 0 la serie est elle nulle ?aviateur a écrit:klaimouad a écrit:la limite de la série converge vers 0
mais cela ne veut rien dire!!!
- 08 Juin 2018, 16:26
- Forum: ✯✎ Supérieur
- Sujet: Analyse fonctionnelle
- Réponses: 8
- Vues: 475
Re: Analyse fonctionnelle
mais eest ce que si la limite de la série converge vers 0 implique que la série est nul ?
- 08 Juin 2018, 16:18
- Forum: ✯✎ Supérieur
- Sujet: Analyse fonctionnelle
- Réponses: 8
- Vues: 475
Re: Analyse fonctionnelle
mais la séparation je n'arrive pas a le faire ?? Qu'est ce que cela veut dire. je veux dire que je n'arrive pas à montrer que d(x,y)=0 \Rightarrow x=y Sinon tu dois utiliser tout simplement: \sqrt{|x-y|}\leq \sqrt{|x-z|}+\sqrt{|z-y|} oui c'est pour montrer l’inégalité triangulaire
- 08 Juin 2018, 16:08
- Forum: ✯✎ Supérieur
- Sujet: Analyse fonctionnelle
- Réponses: 8
- Vues: 475
Re: norme de l'inverse d'une application linéaire
mais est ce que cela est vraie 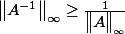
- 08 Juin 2018, 15:06
- Forum: ✯✎ Supérieur
- Sujet: norme de l'inverse d'une application linéaire
- Réponses: 9
- Vues: 1769
Analyse fonctionnelle
Bonjour Notons l^{\frac{1}{2}}=\{ x=(x_n)_{n\in \N } \in \R^{\N} : \sum_{n=0}^{+\infty}{\sqrt{\left|x_n \right|}}<+\infty \} et d(x,y)=\sum_{n=0}^{+\infty}{\sqrt{\left|x_n - y_n \right|}} 1) Montrer que d est une distance sur l^{\frac{1}{2}} (en particulier d est finie ) 2) soit \tau...
- 08 Juin 2018, 15:04
- Forum: ✯✎ Supérieur
- Sujet: Analyse fonctionnelle
- Réponses: 8
- Vues: 475
Re: norme de l'inverse d'une application linéaire
Salut Mimosa si A=\begin{pmatrix} 5 & 0\\ 0 & 6 \end{pmatrix} alors \begin{Vmatrix} A \end{Vmatrix}_{\infty}= max\{5,0,0,6\}=6 Or A^{-1}=\begin{pmatrix} \frac{1}{5} & 0\\ 0 & \frac{1}{6} \end{pmatrix} alors \begin{Vmatrix} A^{-1} \end{Vmatrix}_{\infty}= max\{\frac{1}{5},0,0,\frac{1}{...
- 08 Juin 2018, 14:46
- Forum: ✯✎ Supérieur
- Sujet: norme de l'inverse d'une application linéaire
- Réponses: 9
- Vues: 1769
Re: norme de l'inverse d'une application linéaire
salut non ce n'est pas vraie puisque la dim est fini alors toutes les normes sont équivalente prenant la norme infini alors si A = ( 5 0 0 6 ) alors , norme(A) = 6 et on a A-1 = ( 1/ 5 0 0 1/7 ) et donc norme(A-1) = 1/5 Par contre on a 1/norme(A-1 )<= norme(A) Est-ce que ceci est vraie pour toujours...
- 08 Juin 2018, 13:12
- Forum: ✯✎ Supérieur
- Sujet: norme de l'inverse d'une application linéaire
- Réponses: 9
- Vues: 1769
norme de l'inverse d'une application linéaire
bonjour
soit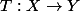 une application linéaire
une application linéaire
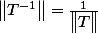 ??
??
soit
- 07 Juin 2018, 19:43
- Forum: ✯✎ Supérieur
- Sujet: norme de l'inverse d'une application linéaire
- Réponses: 9
- Vues: 1769
Differentiel d'une application linéaire
Bonjour soit f : \R^n \rightarrow \R une fonction convexe deux fois différentiable sur \R^n et 0-coercive et A \in M_n(\R) une matrice symétrique définie positive. Pour x\in \R^n posons \phi_x(y)= \frac{1}{2} \left< A(x-y),(x-y) \right>+ f(y) 1) soit x\in\R^n ...
- 02 Juin 2018, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Differentiel d'une application linéaire
- Réponses: 2
- Vues: 390
Re: Fonction caractéristique de loi normale
mercii beaucoup , j'ai pensé en premier à la decomposition en série entiere de exp(itx) mais bon celle là est un meilleur astuce j'ai trouvé exp(- t^2 / 2 )
- 30 Mai 2018, 18:53
- Forum: ✯✎ Supérieur
- Sujet: Fonction caractéristique de loi normale
- Réponses: 2
- Vues: 1593
Fonction caractéristique de loi normale
Bonjour,
comment montrer que la fonction caractéristique d'une variable de loi normale centré est égale à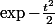
Mercii d'avance
comment montrer que la fonction caractéristique d'une variable de loi normale centré est égale à
Mercii d'avance
- 30 Mai 2018, 08:25
- Forum: ✯✎ Supérieur
- Sujet: Fonction caractéristique de loi normale
- Réponses: 2
- Vues: 1593
Re: Projection sur épigraphe
Ben314 je n'arrive pas à faire un dessin  est je n'arrive non plus à trouver une contradiction de
est je n'arrive non plus à trouver une contradiction de  < \bar{y})
 est je n'arrive non plus à trouver une contradiction de
est je n'arrive non plus à trouver une contradiction de - 29 Mai 2018, 22:17
- Forum: ✯✎ Supérieur
- Sujet: Projection sur épigraphe
- Réponses: 6
- Vues: 515
Re: Projection sur épigraphe
Bonsoir pour montrer l'existance et l'unicité de la projection sur un fermé on utilise le théoreme des fermés emboités qui dit que si un espace métrique est complet alors, pour toute suite décroissante de fermés non vides Fn de E dont le diamètre tend vers zéro, l'intersection des Fn est réduite à u...
- 29 Mai 2018, 22:04
- Forum: ✯✎ Supérieur
- Sujet: Projection sur épigraphe
- Réponses: 6
- Vues: 515
- 52 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
