Salut,
Pseuda a écrit:Bonjour,
Fonction caractéristique de la loi normale ? Si tu veux parler de la fonction de densité, c'est par définition et il manque quelque chose devant.
Nan, c'est bien la fonction caractéristique.
Si X est une variable aléatoire, alors la fonction caractéristique est par définition la fonction notée
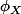
définie pour tout réel t par
 = E(e^{itX}))
(où E désigne espérance). C'est une fonction à valeurs complexes qui caractérise la loi de probabilité de la variable aléatoire.
Ici, si X est une loi normale centrée réduite, elle possède une fonction de densité
= \frac{1}{\sqrt{2 \pi}} e^{-x^2/2})
et donc on peut s'en servir comme calcul d'espérance.
Donc pour tout t,
 =\dfrac{1}{\sqrt{2 \pi}} \int\limits_{-\infty}^{+\infty} e^{itx}e^{-x^2/2}\, \mathrm{d}x =\dfrac{1}{\sqrt{2 \pi}} \int\limits_{-\infty}^{+\infty} e^{itx-\frac{x^2}{2}}\, \mathrm{d}x)
Après, c'est la technique "classique". Tu écris que :
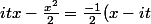^2 - \frac{t^2}{2})
D'où
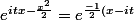^2} \times e^{\frac{-t^2}{2}})
Puis on passe à l'intégrale, on sort le
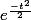
et on calcule classiquement l'intégrale restante qui est du type e^(-X²/2) avec X=x-it (changement de variable qui n'a aucune incidence) et on trouve
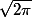
qui s'annule avec le
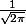
Je te laisse faire les calculs.
Pseudo modifié : anciennement Trident2.