2838 résultats trouvés
Revenir à la recherche avancée
Équivalent suite
Bonsoir, Je cherche à déterminer un équivalent de u_n . J'ai : \ln u_n = \ln n + \dfrac{1}{n} \sum_{k=1}^n \ln(1+\dfrac{k}{n}) J'ai trouvé \lim\limits_{n \rightarrow +\infty} \dfrac{1}{n} \sum_{k=1}^n \ln(1+\dfrac{k}{n})=2 \ln 2 -1 en utilisant les sommes de Riemann. Mais je bloque à...
- 29 Oct 2019, 18:13
- Forum: ✯✎ Supérieur
- Sujet: Équivalent suite
- Réponses: 1
- Vues: 284
Re: Suite non stationnaire
Merci, je suis d'accord l'implication ici complique les choses pour rien.
- 15 Oct 2019, 18:21
- Forum: ✯✎ Supérieur
- Sujet: Suite non stationnaire
- Réponses: 2
- Vues: 548
Suite non stationnaire
Bonsoir,
La suite) est stationnaire si :
est stationnaire si :
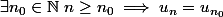
Je traduis le fait qu'une suite n'est pas stationnaire mais je trouve que le résultat n'a aucun sens :
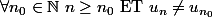


La suite
Je traduis le fait qu'une suite n'est pas stationnaire mais je trouve que le résultat n'a aucun sens :
- 15 Oct 2019, 17:50
- Forum: ✯✎ Supérieur
- Sujet: Suite non stationnaire
- Réponses: 2
- Vues: 548
Re: Théorème de la bijection
Mon livre n'a jamais abordé la notion de convexe. Le théorème dont vous parlez est énoncé ainsi : Les intervalles de \R sont les parties I \subset \R vérifiant : \forall x \in I \ \ \forall y \in I \ [x,y] \subset I Je ne veux pas dénigrer votre travail mais si je ne comprends pas votre démonstratio...
- 16 Sep 2019, 19:38
- Forum: ✯✎ Supérieur
- Sujet: Théorème de la bijection
- Réponses: 24
- Vues: 1712
Re: Continuité
Je ne vois toujours pas.
Mais l'exercice précédent était si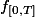 est continue en 0 alors
est continue en 0 alors  est continue sur
est continue sur  .
.
Ici il faut montrer que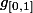 est continue en
est continue en  mais le corrigé étudie la limite de
mais le corrigé étudie la limite de  en
en  et pas en 0
et pas en 0 
Mais l'exercice précédent était si
Ici il faut montrer que
- 15 Sep 2019, 11:00
- Forum: ✯✎ Supérieur
- Sujet: Continuité
- Réponses: 10
- Vues: 569
Re: Théorème de la bijection
Je ne suis pas de mauvaise foi. Mon livre n'a jamais abordé la notion de convexe explicitement pour l'instant. Et si je l'ai utilisé dans des exercices ou problèmes de CAPES je ne l'ai pas remarqué et j'ai mal compris. Avant je faisais des sujets sans connaitre le cours. Je comprends rien dès le dép...
- 15 Sep 2019, 10:26
- Forum: ✯✎ Supérieur
- Sujet: Théorème de la bijection
- Réponses: 24
- Vues: 1712
Re: Continuité
Ok du coup je dois montrer que 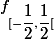 est continue en
est continue en  , alors pourquoi étudier la limite en 1/2 et pas en 0
, alors pourquoi étudier la limite en 1/2 et pas en 0 

- 15 Sep 2019, 10:19
- Forum: ✯✎ Supérieur
- Sujet: Continuité
- Réponses: 10
- Vues: 569
Re: Math 1s
Fais un dessin.
La réponse est dans l'énoncé.
La réponse est dans l'énoncé.
Re: Continuité
regarde la définition de g, c'est f décalée en x de 0.5 (pourquoi faire simple quand on peut faire compliqué) f continue sur ]-1/2; 1/2[ les limites en -1/2+ et 1/2- sont identiques f prolongée par 1 périodicité va être continue sur R entier Oui mais vous n'utilisez pas la restriction de f à [0,1] .
- 14 Sep 2019, 18:56
- Forum: ✯✎ Supérieur
- Sujet: Continuité
- Réponses: 10
- Vues: 569
Re: Continuité
Si g tend vers 1 alors f tend vers 1/2 mais pourquoi étudier la limite en 1/2 pour montrer la continuité en 0 ?
- 14 Sep 2019, 18:55
- Forum: ✯✎ Supérieur
- Sujet: Continuité
- Réponses: 10
- Vues: 569
- 14 Sep 2019, 17:44
- Forum: ✯✎ Supérieur
- Sujet: Racines 5iemes MPSI
- Réponses: 10
- Vues: 775
Re: Continuité
Je n'ai pas compris pourquoi pour montrer que 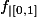 est continue en
est continue en  on étudie la limite en
on étudie la limite en  et pas en
et pas en 

Et pourquoi on décale de 1/2
de 1/2 

Et pourquoi on décale

- 14 Sep 2019, 17:21
- Forum: ✯✎ Supérieur
- Sujet: Continuité
- Réponses: 10
- Vues: 569
Re: Théorème de la bijection
C'est pas de mon niveau votre démonstration. Je suis perdu dès la première ligne. En la lisant, je sais que je n'ai pas du tout le niveau pour la comprendre, en plus je n'ai pas vu les convexes. Je remettrai de façon claire celle de mon livre où j'ai réussi à presque tout comprendre sauf les 3 derni...
- 14 Sep 2019, 09:33
- Forum: ✯✎ Supérieur
- Sujet: Théorème de la bijection
- Réponses: 24
- Vues: 1712
Continuité
Bonjour, 1/ Justifier qu'il existe une unique fonction réelle définie sur \R qui soit 1-périodique et telle que : \forall x \in [-\dfrac{1}{2},\dfrac{1}{2}[ \ f(x)=|x| 2/ Démontrer que f_{|[0,1]} est continue en 0 . D'après un exercice vu précédemment, cela signifie que f est continue. Unici...
- 14 Sep 2019, 09:27
- Forum: ✯✎ Supérieur
- Sujet: Continuité
- Réponses: 10
- Vues: 569
Re: Fonction constante
J'ai corrigé ma coquille avec l'inégalité stricte dans mon message précédent. Il n'y a donc pas besoin de prendre les \alpha_k distincts au départ. J'ai fait le dessin j'ai compris. Je l'ai aussi démontré par le calcul : \forall x \in \R \ x-nT_n \in [0,T] pour n=E(\dfrac{x}{T}) En effet, 0 ...
- 14 Sep 2019, 09:14
- Forum: ✯✎ Supérieur
- Sujet: Fonction constante
- Réponses: 18
- Vues: 801
Re: sommes telescopique
Salut. (a-b) \sum_{k=0}^{n-1} a^k b^{n-k-1} =\sum_{k=0}^{n-1} (a^{k+1}b^{n-k-1} - a^k b^{n-k}) Soit : (a-b) \sum_{k=0}^{n-1} a^k b^{n-k-1} =\sum_{k=0}^{n-1} (a^{k+1}b^{n-(k+1)} - a^k b^{n-k})=\sum_{k=0}^{n-1} a^{k+1}b^{n-(k+1)} - \sum_{k=0}^{n-1} a^{k}...
- 14 Sep 2019, 08:30
- Forum: ✯✎ Supérieur
- Sujet: sommes telescopique
- Réponses: 5
- Vues: 633
Re: Fonction constante
Je remets tout. J'ai très bien compris la correction de la question 1, il y a un point qui me bloque dans celle de la question 2. 1/Les n+1 valeurs des \alpha_k sont dans [0,1[ . On peut réordonner de manière croissante ces valeurs. Cela nous donne \beta_0 , \beta_, \cdots \beta_n avec \beta_0 \leq ...
- 14 Sep 2019, 02:35
- Forum: ✯✎ Supérieur
- Sujet: Fonction constante
- Réponses: 18
- Vues: 801
Re: Fonction constante
D'accord Kolis, je ferais ça. La solution de Tuvasbien avait l'air plus compliquée que celle de mon livre. Je n'ai pas compris pourquoi : |x-x_n| \leq |T_n| \leq \dfrac{1}{n} :?: Vous utilisez que x_n tend vers 0 pour montrer que f(x)=f(0) ? La première question a été résolue différe...
- 13 Sep 2019, 10:35
- Forum: ✯✎ Supérieur
- Sujet: Fonction constante
- Réponses: 18
- Vues: 801
Re: Fonction constante
Il n'y a pas une coquille ?
C'est pas plutôt :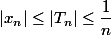 donc
donc 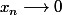
Au lieu de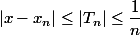 ?
?
C'est pas plutôt :
Au lieu de
- 12 Sep 2019, 19:55
- Forum: ✯✎ Supérieur
- Sujet: Fonction constante
- Réponses: 18
- Vues: 801
Re: Eprimer Sn en fonction de n
Tu peux vérifier qu'on obtient le résultat suivant.
 = \sum_{k=0}^n k + \sum_{k=0}^n 1 = \dfrac {n(n+1)}{2} + (n+1))
Donc (\dfrac{n}{2}+1})=\dfrac{1}{2} (n+1)(n+2))
Donc
- 12 Sep 2019, 19:15
- Forum: ✎✎ Lycée
- Sujet: Eprimer Sn en fonction de n
- Réponses: 10
- Vues: 3039
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
