Il semblerait que tu n'as pas le courage de faire cette démonstration dans le même style que ton fameux livre !
Je me permets de te donner une solution assez simple où on n'a pas besoin de jongler avec les comparaisons des images de deux ou trois termes :

est un intervalle de réels,

est continue sur

et injective.
Soit
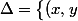\in I^2\;\mid\;x<y\bigr\})
. Selon que

a 0,1,2 bornes finies,

est un demi-plan ou intersection de deux demi-plans ou intersection de trois demis-plans.
En particulier,

est un convexe de
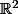
.
La relation
=\dfrac{f(x)-f(y)}{x-y})
définit une fonction continue sur

et on se propose de démontrer que
)
est un convexe de

.
Pour cela, soit
\in(\Phi(\Delta))^2,\;u<w<v)
. Par exemple,
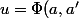,\;v=\Phi(b,b'),\;(a,a')\in\Delta,\;(b,b')\in\Delta)
.
Soit
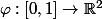
telle que
=(1-t)(a,a')+t(b,b'))
.

est continue sur

, à valeurs dans

à cause de la convexité.
Par conséquent,
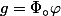
est continue sur

à valeurs réelles et
=\Phi(\varphi(0))=\Phi(a,a')=u,\;g(1)=v)
.
Par théorème des valeurs intermédiaires il existe
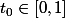
tel que
=w)
. En posant
=\varphi(t_0))
on a
\in\Delta,\;w=g(t_0)=\Phi(c,c')\in\Phi(\Delta))
.
Enfin l'injectivité de

implique
)
.
Ainsi, on a un convexe de

ne contenant pas

: il est forcément inclus dans
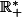
ou
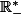
. J'ai ainsi démontré que

est strictement monotone.
