slt j'aimerais que vous m'eclairer sur cet exercice depuis troi jours je galere la dessus
soit (un)n>=1 a termes positives tel que somme des (un),n>=1 converge.
a)on suppose que (un)n>=1 decroit .
1) demontrer que lim n->+infini nUn=0
2)en deduire la nature des series somme des nU²n n>=1et somme des Un/1-nUn n>=1
b) montrer par un contre exemple que le resultat du a) n'est plus vrai si la (Un)n>=1n'est pas supposée croissante
Series numeriques exo
9 messages
- Page 1 sur 1
chipiniane a écrit:slt j'aimerais que vous m'eclairer sur cet exercice depuis troi jours je galere la dessus
soit (un)n>=1 a termes positives tel que somme des (un),n>=1 converge.
a)on suppose que (un)n>=1 decroit .
1) demontrer que lim n->+infini nUn=0
2)en deduire la nature des series somme des nU²n n>=1et somme des Un/1-nUn n>=1
b) montrer par un contre exemple que le resultat du a) n'est plus vrai si la (Un)n>=1n'est pas supposée croissante
help me j vw rien juska presen
Bonjour,
Je pose , on a
, on a  . Chaque terme de cette dernière somme peut être minoré par
. Chaque terme de cette dernière somme peut être minoré par 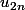 puisque la suite est décroissante. Donc
puisque la suite est décroissante. Donc  d'où
d'où \geq 2nu_{2n}) et comme la série converge, on a tout de suite
et comme la série converge, on a tout de suite \longrightarrow\limits_{n\to\infty}0) . Reste à montrer que
. Reste à montrer que u_{2n+1}\longrightarrow\limits_{n\to\infty}0) mais cela est facile puisque
mais cela est facile puisque u_{2n+1}\leq(2n+1)u_{2n}=2nu_{2n}+u_{2n}) (je te laisse finir les détails)
(je te laisse finir les détails)
Ensuite c'est encore plus simple :
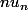 tend vers zéro, donc
tend vers zéro, donc 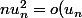) , puis conclure...
, puis conclure...
Ensuite : tend vers 1 donc
tend vers 1 donc  , puis conclure.
, puis conclure.
Pour le b) un contre-exemple classique devrait suffire...
Je pose
Ensuite c'est encore plus simple :
Ensuite :
Pour le b) un contre-exemple classique devrait suffire...
@chipiniane
Si une suite (un) est positive , converge et décroit alors tout ce qu'on peut dire :
c'est que si on note la limite de
la limite de  quand
quand  tend vers +infini
tend vers +infini
1) on sait que
2) pour tout on a :
on a : 
3) Et on peut en déduire que :
pour tout n on a :
Conclusion :
si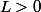 , la suite (
, la suite () tend vers +infini quand n tend vers + infini
tend vers +infini quand n tend vers + infini
si : on ne peut rien conclure (avec cette méthode)
: on ne peut rien conclure (avec cette méthode)
Si une suite (un) est positive , converge et décroit alors tout ce qu'on peut dire :
c'est que si on note
1) on sait que
2) pour tout
3) Et on peut en déduire que :
pour tout n on a :
Conclusion :
si
si
D'après moicuati a écrit:Salut Ptitnoir,
je ne comprends pas trop ta remarque... en quoi aide-t-elle à résoudre l'exercice ?
est FAUXchipiniane a écrit:1) demontrer que lim n->+infini nUn=0
ou sinon j'ai du loupé "un truc" dans l'énoncé de cet exo
Aussi je te remercie de bien vouloir m'expliquer où est mon erreur ?
ptitnoir a écrit:D'après moi
est FAUX
ou sinon j'ai du loupé "un truc" dans l'énoncé de cet exo
Aussi je te remercie de bien vouloir m'expliquer où est mon erreur ?
Je pense que tu as mal lu l'énoncé, la suite
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
