Mystere mathematique > Series numeriques

[Lyloern]

Bonjour a vous,

J'ai un petit probleme sur une suite numerique. Dans le cours et dans la resolution de l'exercice (correction), on a :
Si (n^alpha).Un tend vers 0, alors si alpha > 1 => la suite Converge. OK.

J'ai maintenant l'exerice suivant :

Un = (ln(n))^(-Racine(n))

La correction de la prof dit (ou mon interpretation de sa correction) :

n².Un => n².(ln(n))^(-Racine(n)) = n².e^(-Racine(n).ln(ln(n))
l'expression de l'exponentiel tend vers -infini donc le e tend vers 0. Par croissance comparée, on a le tout qui tend vers 0 et alpha > 1 (2>1) donc la suite est convergent...

questions :

1) D'ou on rajoute un n² comme ca, gratuitement !?
2) On choisit un alpha = 2, ca nous arrange bien pour la fin puisque 2 > 1 mais pourquoi on aurait pas pu mettre n^1 ?
3) quel est ce mystere mathematiques ? A quoi sert ce n^alpha sans qui, on aurait aussi e qui tend vers 0 et ca ne changerait rien a notre histoire (oui alpha > 1 mais c'est nous qui lavons inventé ce alpha!)

Merci d'avance ! :D

[Arnaud-29-31]

Salut,

Si (n^alpha).Un tend vers 0, alors si alpha > 1 => la suite Converge. OK.

Tu voulais dire la série converge, je suppose ...

On rajoute le n² gratuitement car c'est un avec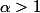
Je ne comprend pas ta deuxième question, si on met , ca ne nous apportera rien de dire que tend vers 0 puisque la propriété s'applique pour .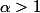


Pour reprendre les choses :

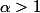Si tend vers 0 alors on peut écrire et donc est négligeable devant . Et tu n'es pas sans savoir que la série des est convergente ssi (séries de Riemann).

Donc pour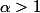, le terme de notre série est négligeable devant le terme générale d'une série convergente , et donc notre série converge.

EDIT : Oui, bien sur :s c'est corrigé ;pp

[Doraki]

2) On choisit un alpha = 2, ca nous arrange bien pour la fin puisque 2 > 1 mais pourquoi on aurait pas pu mettre n^1 ?

Obtenir que n*Un tend vers 0, c'est "moins fort" que obtenir que n²*Un tend vers 0.
Plus tu réussis à mettre un alpha grand, plus ça dit que ta suite converge "rapidement" vers 0.

Dans ton cas ici, non seulement alpha 2 marche, mais comme tu as remarqué, n'importe quel alpha marche, en particulier pour n'importe quel alpha aussi grand que tu veux (alpha = 1 on s'en fout)
Ta suite Un décroit plus vite que n'importe quelle suite 1/n^alpha, même avec alpha = 1000, un million, etc.

[Lyloern]

Ok je vois!