Démonstration par l'absurde : mon avis... et le vôtre ?

[leon1789]

normalement ca donne pas un résultat, mais le résultat, mais s'il est donné, il n'y a pas lieu d'aller chercher plus loin.

Oui je voulais dire le résultat (j'ai corrigé, merci).

Sinon, dans un soucis d'amélioration, je pense qu'il y a toujours à retravailler une chose qu'on vient juste de réaliser pour la première fois : un algorithme, une dissertation, une preuve, etc.

[Ourfalli]

J'ai suivi avec intérêt votre discussion.Si on se pose la question sur l'utilité réelle de la démonstration par l'absurde, je peux en suggérer deux :

Premièrement, la méthode de démonstration adoptée implique souvent choix de notation mathématique, ce choix est souvent crucial dans la clarté de l'exposé et la simplicité des calculs.

Il n'est pas inutile de jeter un coup d'œil sur "la théorie des ensembles de Bourbaki" notamment dans le chapitre "Théories logiques" où il apporte un regard très riche sur l'axiomatique et les raisonnements qui en résultent.

Deuxièmement, il me semble que la preuve par l'absurde est une situation qui décrit assez bien les mécanismes de l'apprentissage. Comment ?

Si les mathématiques ont comme but, entre autres, de construire des vérités abstraites sur des réalités observées, autrement dit modéliser le réel, alors il faut s'attendre à des situations ou cette vérité est mise en cause par un paradoxe observé (exemple : l'insuffisance des nombres rationnels pour décrire les longueurs, le paradoxe de Bertrand,...).

Le mot clé de cette mise en cause est le paradoxe .toute situation d'apprentissage confronte l'élève ou le chercheur à une situation de déséquilibre initial qui sera surmonté par une nouvelle reconstitution de la réalité étudiée. (cf. "l'école pour apprendre", de Jean-Pierre Astolfi).

Donc, l'utilité d'une démonstration par l'absurde peut avoir un intérêt pédagogique pour inciter l'élève à se poser des questions mathématiciennes.

Mais attention ! il faut toujours avoir dans l'esprit les axiomes fondateurs de notre raisonnement. Un mathématicien se méfie de l'évident et encore plus de ce qui est évidemment absurde.

[leon1789]

Merci de prendre part à la discussion.

J'ai suivi avec intérêt votre discussion.Si on se pose la question sur l'utilité réelle de la démonstration par l'absurde, je peux en suggérer deux :

Premièrement, la méthode de démonstration adoptée implique souvent choix de notation mathématique, ce choix est souvent crucial dans la clarté de l'exposé et la simplicité des calculs.

Oui, juste au-dessus, le choix de ffpower confirme cette idée.

Il n'est pas inutile de jeter un coup d'œil sur "la théorie des ensembles de Bourbaki" notamment dans le chapitre "Théories logiques" où il apporte un regard très riche sur l'axiomatique et les raisonnements qui en résultent.

Deuxièmement, il me semble que la preuve par l'absurde est une situation qui décrit assez bien les mécanismes de l'apprentissage. Comment ?

Si les mathématiques ont comme but, entre autres, de construire des vérités abstraites sur des réalités observées, autrement dit modéliser le réel, alors il faut s'attendre à des situations ou cette vérité est mise en cause par un paradoxe observé (exemple : l'insuffisance des nombres rationnels pour décrire les longueurs, le paradoxe de Bertrand,...).

Le mot clé de cette mise en cause est le paradoxe .toute situation d'apprentissage confronte l'élève ou le chercheur à une situation de déséquilibre initial qui sera surmonté par une nouvelle reconstitution de la réalité étudiée. (cf. "l'école pour apprendre", de Jean-Pierre Astolfi).

je crois comprendre vaguement...

Donc, l'utilité d'une démonstration par l'absurde peut avoir un intérêt pédagogique pour inciter l'élève à se poser des questions mathématiciennes.

...mais là, je ne vois pas le rapport avec le paragraphe précédent.

Le fait que le raisonnement par l'absurde soit utile ne fait pas de doute. Mais les questions (modestes !) pédagogiques que je me permets de vous soumettre sont celles-ci.

-- Les élèves comprennent-ils plus facilement un raisonnement direct, avec discussion, par contraposition, par l'absurde ? (je pense que ce dernier reste le moins "apprécié".)

-- Doit-on se satisfaire d'une preuve par l'absurde comme rédaction finale ? (votre premier argument indique "parfois oui", mais sauf cas contraire exceptionnel, je pense que non.)

-- Ne fait-on pas trop souvent appel (inutilement) au raisonnement par l'absurde ?

-- Il y a-t-il une différence entre raisonnement par l'absurde et par contraposée ? (par exemple, en géométrie, une preuve par l'absurde se fait forcément sur un dessin "faux" alors qu'une contraposée peut se faire sur un dessin "juste" puisque c'est une preuve directe de "non B => non A", voir par exemple http://www.maths-forum.com/showpost.php?p=576163&postcount=46)

[Ourfalli]

Je vous prie de m'excuser, parfois il me semble que ce que je dit est clair alors qu'il ne l'est pas!

Je fait le parallélisme entre la preuve par absurde et le paradoxe qui peut nous amener à savoir plus sur une question ou phénomène étudié.

Par exemple :
Historiquement, Pythagore est le premier à faire face à l'énorme paradoxe de la [url="http://www.col-camus-soufflenheim.ac-strasbourg.fr/Page.php?IDP=84&IDD=0"]pentagrame enchevétrée[/url], symbole de la Fraternité pythagoricienne.
Il avait la certitude que l'enchevêtrement de ces figures est fini, ce qui est faux. Cela a mis fin à son l'école qui affirmait que Tout est nombre (rationnel).

Proposer aux élèves des situations expérimentales où ils tomberons eux mêmes dans ce paradoxe historique puis leur proposer des outils adéquates de réflexion (entre autres la preuve par l'absurde de l'impossibilité ), permet (à mon avis) aux élèves de rejeter (eux mêmes) l'hypothèse "tout est nombre" et réinventer le concept des nombre réels.

Permettez-moi de répondre à vos questions :

-- La démonstration par absurde est la moins appréciée, si elle est présentée comme la seul manière d'aboutir à la finalité "tout nombre n'est pas rationnel".

-- Je comprends votre insatisfaction vis à vis la preuve par absurde, si la rédaction ne permet pas de voir le cheminement de la pensée, si l'absurde qu'elle provoque n'est pas facile à comprendre ou compliqué, alors il est certain qu'une démonstration directe ou par contraposition est la bienvenue.
Donc, parfois oui, mais sous réserve de clarté et de rigueur, la question que je vous pose est : pensez-vous que la démonstration par absurde conduit à une manque de rigueur dans la démonstration ou dans sa rédaction?

-- Je pense qu'il est possible que ce choix soit pris par facilité au détriment de la rigueur ou la clarté.
En tout cas je pense qu'il est utile pour un mathématicien d'être capable de proposer plusieurs styles de rédaction d'une démonstration, ce n'est qu'un enrichissement de sa "boîte à outils".

-- Parlons de la géométrie. Un dessin précis reste un choix favori dans le cas d'une démo directe. Dans le cas de l'absurde il peut conduire à une impossibilité de construction, ce que vous dites exactement au sujet de la trajectoire de billard.

Mais la différence essentielle entre les deux méthodes de démonstration est que dans la contraposition on n'a pas besoin d'une troisième proposition R telle que et soient vraies simultanément, c'est l'avantage de la démo directe ou par contraposition, c'est plus économique.

[leon1789]

-- La démonstration par absurde est la moins appréciée, si elle est présentée comme la seule manière d'aboutir à la finalité "tout nombre n'est pas rationnel".

Vous voulez dire que, sans une pratique relativement fréquente, la démonstration par absurde resterait la moins appréciée ?

Donc, parfois oui, mais sous réserve de clarté et de rigueur, la question que je vous pose est : pensez-vous que la démonstration par absurde conduit à une manque de rigueur dans la démonstration ou dans sa rédaction ?

Dans le cadre de l'apprentissage (c'est notre cadre), je crois que la démonstration par absurde est un outil supplémentaire à ne pas négliger, mais cet outil tend un piège : c'est celui de casser volontairement le garde-fou de la non-contradiction des maths. Dans une preuve non-contradictoire (directe, discussion, récurrence, contraposée), un élève arrivant à une contradiction se posera naturellement (normalement...) la question : ha, mais où est l'erreur ? Dans une preuve par l'absurde, arrivant à une contradiction, l'élève sera content... en minimisant complètement le risque que cette contradiction provienne d'une erreur de raisonnement ou de calcul.
Alors, pour répondre à votre question : non, je ne crois pas que la démonstration par absurde conduise à une manque de rigueur dans la démonstration ou dans sa rédaction, mais entraîne un risque supplémentaire d'erreur.
(Je ne veux pas dire que toutes les preuves non-contradictoires sont toujours justes, évidemment.)

De plus, une preuve non-contradictoire peut être "vérifiée" à l'aide d'un (ou plusieurs) exemple(s). Cela permet de rassurer l'élève auteur de la preuve, ou bien d'infirmer sa preuve le cas échéant. Il me parait difficile de faire la même chose avec une preuve par l'absurde, par nature même de cette preuve... Ce fait augmente encore indirectement le risque d'erreur non détectée.

En tout cas je pense qu'il est utile pour un mathématicien d'être capable de proposer plusieurs styles de rédaction d'une démonstration, ce n'est qu'un enrichissement de sa "boîte à outils".

Pas de doute.

Mais la différence essentielle entre les deux méthodes de démonstration est que dans la contraposition on n'a pas besoin d'une troisième proposition R telle que et soient vraies simultanément, c'est l'avantage de la démo directe ou par contraposition, c'est plus économique.

Oui, j'ai ce point de vue aussi (par exemple http://www.maths-forum.com/showpost.php?p=416190&postcount=90)

[Ourfalli]

Je suis d'accord que :

Dans une preuve par l'absurde, arrivant à une contradiction, l'élève sera content... en minimisant complètement le risque que cette contradiction provienne d'une erreur de raisonnement ou de calcul.

Enfin, on peut discuter comme ça à l'infini, c'est passionnant.
Personnellement, j'en tire les conclusions suivantes :

1. Un choix de démonstration ou de rédaction prend en compte que l'on ne démontre pas qu'à soi-même.
2. Il est bon de varier ses techniques au maximum.
3. Il faut s'entraîner suffisamment pour ne plus confondre entre un paradoxe d'une démonstration par absurde et une erreur de raisonnement.

Pour finir, voici une citation tirée de l'œuvre des Bourbaki "Éléments de Mathématique, Théorie des Ensembles" (Ed. Springer, Introduction, page I.12):

Qu'une théorie soit contradictoire revient en effet à dire qu'elle comporte une démonstration formalisée correcte aboutissant à la conclusion

[leon1789]

Lien entre récurrence et raisonnement par l'absurde : http://www.maths-forum.com/showthread.php?t=89596

[leon1789]

Bonsoir, et bonne année à tous ! :we: :we:

Ce soir, j'apporte un exemple un peu extra-mathématique pour montrer (je ne dis pas "démontrer") qu'un raisonnement par l'absurde [Prop1 et non Prop2 => contradiction] signifie une implication moins forte qu'une preuve directe [Prop1 => Prop2].

Mon illustration s'appuie sur une étude d'une grille de sudoku. Ci-dessous, je présente un tableau (neuf colonnes de 1 à 9, neuf lignes de A à I, neuf blocs carrés) de candidats :

Code: Tout sélectionner

     1     2     3       4       5      6       7      8      9
+--------------------+---------------------+---------------------+
|      1   458  4689 |   3568  23589 35689 |    2349   239     7 | A
|    589     2   789 |      4 135789 35789 |     139     6   189 | B
|   4689   478     3 |   1678  12789  6789 |       5   129 12489 | C
+--------------------+---------------------+---------------------+
|  23568     9 12678 |  13578      4  3578 |   12367 12357  1256 | D
|    358 13578   178 |  13578      6     2 |      39     4    59 | E
|  23456 13457 12467 |      9   1357   357 |       8 12357  1256 | F
+--------------------+---------------------+---------------------+
|   2489   148     5 |    678    789 46789 |  124679  1279     3 | G
|    349     6   149 |      2   3579 34579 |    1479     8  1459 | H
|      7   348  2489 |   3568   3589     1 |    2469   259 24569 | I
+--------------------+---------------------+---------------------+


Par exemple, la case A1 contient seulement le chiffre 1 ;
la case A2 contient l'un des chiffres 4,5,8 (il reste à déterminer lequel) ;
... la case I9 contient l'un des chiffres 2,4,5,6,9 (il reste à déterminer lequel).

Voici les deux propositions :
Prop1 = "la solution fait apparaître le chiffre 3 dans la case D4"
Prop2 = "la solution fait apparaître le chiffre 3 dans la case E7"

Je ne rappelle pas les règles du sudoku (j'imagine que tout le monde les connaît) et je ne vous donne pas non plus la solution de ce sudoku (je vous souhaite bon courage pour la trouver à la main). :ptdr:

Je voudrais juste constater deux faits :
-1- On montre assez facilement que l'hypothèse "Prop1 et non Prop2" amène à une contradiction ;
-2- Et pourtant l'hypothèse Prop1 seule n'amène pas à Prop2 !
(...et d'ailleurs l'hypothèse "non Prop2" n'amène pas non plus à "non Prop1"...)


Je prouve le fait -1- :
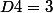
supposons "Prop1 et non Prop2 " et je regarde ce qui arrive...

Code: Tout sélectionner

     1     2     3       4       5      6       7      8      9
+--------------------+--------------------+---------------------+
|      1   458  4689 |   568  23589 35689 |    2349   239     7 | A
|    589     2   789 |     4 135789 35789 |     139     6   189 | B
|   4689   478     3 |  1678  12789  6789 |       5   129 12489 | C
+--------------------+--------------------+---------------------+
|   2568     9 12678 |     3      4   578 |    1267  1257  1256 | D
|    358 13578   178 |  1578      6     2 |       9     4    59 | E
|  23456 13457 12467 |     9    157    57 |       8 12357  1256 | F
+--------------------+--------------------+---------------------+
|   2489   148     5 |   678    789 46789 |  124679  1279     3 | G
|    349     6   149 |     2   3579 34579 |    1479     8  1459 | H
|      7   348  2489 |   568   3589     1 |    2469   259 24569 | J
+--------------------+--------------------+---------------------+


E7=9 (candidat unique),
E9=5 (candidat unique),
I8=5 (unique 5 en colonne),
A4=5 (unique 5 en colonne),
B1=5 (unique 5 en ligne),
F2=5 (unique 5 en colonne),
multiples placements évidents par candidat unique,
D8=7 (unique 7 en colonne),
F8=3 (unique 3 en ligne),
G7=6 (unique 6 en ligne),
G8=1 (unique 1 en colonne),
H5=5 (unique 5 en ligne),
H6=3 (unique 3 en ligne),
H7=7 (unique 7 en ligne),
I2=3 (unique 3 en colonne),
E2=1 (unique 1 en colonne),
E3=7 (unique 7 en ligne),
G1=2 (unique 2 en ligne),
G6=4 (unique 4 en colonne),
H3=1 (unique 1 en ligne),
multiples placements évidents par candidat unique,
et on arrive à une impossibilité... par exemple deux fois le chiffre 2 en première ligne

Code: Tout sélectionner

+--------------+--------------+--------------+
|    1   4 689 |    5   3 689 |    2   2   7 |
|    5   2  89 |    4   7  89 |   13   6  18 |
|   68   7   3 |    1   2  68 |    5   9  48 |
+--------------+--------------+--------------+
|   68   9 268 |    3   4   5 |   12   7 126 |
|    3   1   7 |    8   6   2 |    9   4   5 |
|   46   5 246 |    9   1   7 |    8   3  26 |
+--------------+--------------+--------------+
|    2   8   5 |    7   9   4 |    6   1   3 |
|   49   6   1 |    2   5   3 |    7   8  49 |
|    7   3  49 |    6   8   1 |   24   5 249 |
+--------------+--------------+--------------+


Conclusion : Prop1 et non Prop2 => contradiction


Maintenant, je "prouve" le fait -2- :
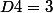
supposons seulement Prop1 et regardons ce qui arrive sur le tableau initial... Ben rien n'arrive ! :doh: Nothing at all !

supposons seulement "non Prop2" , et regardons sur le tableau initial. Il vient
E7=9 (candidat unique),
E9=5 (candidat unique),
I8=5 (unique 5 en colonne),
et c'est à peu près tout.

Conclusion : Prop1 n'implique pas Prop2,
et "non Prop2" n'implique pas "non Prop1".

A chacun de voir en quoi on peut croire réellement à
[ X et non Y => faux ] ==> [ X => Y ]
:zen:







(...si j'ai pu faire naître des vocations sur le sudoku :+++:)

[ffpower]

J ai pas encore lu ton post, mais en tout cas, bon retour, ca fait longtemps qu'il n y a pas eu de débat acharné sur le raisonnement par l'absurde( ca me manquait :triste: )..
Et accessoirement, bonne année aussi

[ffpower]

Bon bah maintenant j ai lu (enfin pas en détail^^)
Au passage j aime bien le fait que t aies tripé sur tes raisonnements par l absurde alors que tu te faisais tranquille un sudoku dans le métro ou je ne sais ou..

Mais pour moi, la, ce que tu a prouvé, c est qu un raisonnement par l absurde est plus efficace qu un raisonnement direct. Et ca je suis tout a fait d accord. C est toujours mieux de raisonner par l absurde, ca fait plus d hypotheses.
Mais vu qu a priori ton but, c est justement de montrer que l absurde, c est moins efficace car on obtient moins d infos a la fin, ben du coup je vois pas trop ou tu voulais en venir..

[Ben314]

Bonsoir à tous,
Je n'ais pas trop d'opinion sur les preuves par l'absurde (les tables de vérité de P=>Q et de non(P et non(Q)) étant les mêmes...)

Par contre je suis quasi sûr que le sudoku ci dessus n'a pas de solution...

[Nightmare]

A chacun de voir en quoi on peut croire réellement à
[ X et non Y => faux ] ==> [ X => Y ])

En particulier vrai lorsque X est faux ...

[leon1789]

Bonsoir à tous,
Je n'ais pas trop d'opinion sur les preuves par l'absurde (les tables de vérité de P=>Q et de non(P et non(Q)) étant les mêmes...)

A ton avis, si on a une preuve de [A et non B => faux] sous les yeux, peut-on toujours en déduire [A => B] ? c'est psychologiquement un problème, je trouve.

Par contre je suis quasi sûr que le sudoku ci dessus n'a pas de solution...

Pourquoi ?

Il y a une solution unique qui est

159826437
827453961
643719528
291348756
578162349
436975812
915684273
364297185
782531694

[leon1789]

En particulier vrai lorsque X est faux ...

Oui, je suis d'accord... en théorie.
Mais en pratique, voit-on des théorèmes qui admettent des hypothèses X fausses pour en déduire une conclusion Y ?

(En passant, sur mon histoire de sudoku, X est vrai en fait, mais il faut le démontrer sans l'admettre :we: )

Pour moi, un théorème est un résumé de la démonstration qu'on en donne, autant dans les hypothèses et conclusions, que dans le sens de la preuve :
en clair,
si la preuve montre [A => B] alors je pense qu'il faut énoncer le théorème [A => B].
si la preuve montre [non B => non A] alors je pense qu'il faut énoncer le théorème [non B => non A].
si la preuve montre [A et non B => faux] alors je pense qu'il faut énoncer le théorème [A et non B n'est pas possible].
Comme ça, la preuve est toujours une preuve directe du théorème ! :zen:

[leon1789]

Bon bah maintenant j ai lu (enfin pas en détail^^)

Allez, faut se mettre au sudoku ! :ptdr:

Au passage j aime bien le fait que t aies tripé sur tes raisonnements par l absurde alors que tu te faisais tranquille un sudoku dans le métro ou je ne sais ou..

Depuis quelques mois, je me suis penché (de manière amatrice et artisanale) sur la résolution de sudokus les plus difficiles qu'on ait trouvés.... ben, ils sont franchement difficiles (!) et je n'ai pas encore trouvé le truc miracle :ptdr:

Mais pour moi, la, ce que tu a prouvé, c est qu un raisonnement par l absurde est plus efficace qu un raisonnement direct. Et ca je suis tout a fait d accord. C est toujours mieux de raisonner par l absurde, ca fait plus d hypotheses.
Mais vu qu a priori ton but, c est justement de montrer que l absurde, c est moins efficace car on obtient moins d infos a la fin, ben du coup je vois pas trop ou tu voulais en venir..

Oui, c'est un fait que le raisonnement par l'absurde permet de raisonner plus facilement (et non "efficacement") car il part avec davantage d'hypothèses. J'ai toujours été d'accord avec cela, et d'ailleurs, je fais des raisonnements par l'absurde au brouillon. Mais seulement au brouillon : pourquoi ? C'est justement parce que cette plus grande facilité apporte moins d'informations finalement (cela peut paraître douteux et vicieux, mais c'est finalement tout de même un peu moral :id: si on paie moins cher, c'est qu'il y a moins de légumes dans le panier).

En effet, de manière théorique, posons
theo1 : [A => B]
theo2 : [A et non B => faux]
On a theo1 => theo2 (si A => B, alors A et non B => B et non B => faux)
mais pas réciproquement (si A et non B => faux, alors A seul n'implique rien :
mon histoire de sudoku essaie d'illustrer cela, même si c'est très critiquable).
On peut donc dire que le theo1 est plus fort que le theo2.

En pratique, (je reprends mon refrain :ptdr: ,) par exemple,
les assertions d'une preuve par l'absurde ne sont jamais réutilisables (puisqu'on ne connait pas leur valeur de vérité), alors que les assertions d'une preuve directe sont toujours réutilisables car vraies (sous couvert des hypothèses bien sûr).
Par ailleurs, autant transformer une preuve directe en une preuve par l'absurde n'a aucun intérêt (puisque c'est instantané), ré-écrire une preuve par l'absurde sous une forme directe permet parfois d'améliorer les choses (au niveau précision du résultat ou de la forme).

[Ben314]

Il me semble que le 3 en E7 n'était pas dans le problème de départ...
159826437
827453961
643719528
291348756
578162349
436975812
915684273
364297185
782531694

J'ai fait un petit programme de sudoku qui les analyse, en fabrique de nouveaux (la difficulté est à choisir) et qui aide à les résoudre.
Si ça interesse quelqu'un, je le donne : le source est en C++ et il fonctionne sous environement windows, mais comme il date un peu, il faut des fois "simuler" du windows un peu ancien. Par contre, je ne sais pas où le mettre pour le donner...

Concernant les preuves par l'absurde, ma remarque voulait juste dire qu'au niveau "logique formelle usuelle" il n'y a pas de différence entre (P=>Q) et non(P et non(Q)) et donc que pour trouver des différences il faut soit employer d'autres formes de logique (constructiviste par exemple) ou bien (et c'est ce tu précise dans ton post) se placer d'un point de vue "psychologique".
Je n'ai pas lu tout les posts de la discution (23 pages...) mais quelques unes et je rejoint un bon nombre de commentaires déjà fait :

Une des choses qui me gène (psychologiquement) le plus dans les preuves par l'absurde, c'est le fait que les étudiants en sont "friands" et qu'ils les utilisent trés (trop) souvent. Je me suis souvent demandé si cela ne venait pas du fait que, dés la première erreur de calcul ou de raisonnement, on tombe sur une contradiction et ... c'est gagné puisque c'est ce que l'on voulais avoir.

La deuxième chose, (plus sérieusement), est évidement le fait que, dans une preuve par l'absurde, on a pas vraiment de support de raisonnement, je pense en particulier à la géométrie : quel dessin faire dans une preuve par l'absurde ? Je pense que Math.=Intuition+Formalisme et le coté Intuition dans les preuves par l'absurde...

P.S. Pour le sudoku, je me demande si je ne suis pas parti d'une des grilles du bas du post. qui sont... contradictoires....

[Ben314]

Je confirme que c'est moi qui me suis gourré dans la saisie du sudoku.
Ta grille a bien une unique solution et il n'y a aucune case qu'un raisonement "direct" permet de remplir (et il y a 15 raisonnement possibles conduisant à deux choix...)

Encore désolé...

P.S. La grille est effectivement considérée comme "extrèmement difiçile" par mon programme....

[leon1789]

Il me semble que le 3 en E7 n'était pas dans le problème de départ (...) Je confirme que c'est moi qui me suis gourré dans la saisie du sudoku.

Faut arrêter de boire du champagne (restant des fêtes de fin d'année) à jeun dès le matin comme ça ! :ptdr:

Ta grille a bien une unique solution et il n'y a aucune case qu'un raisonement "direct" permet de remplir (et il y a 15 raisonnement possibles conduisant à deux choix...)

P.S. La grille est effectivement considérée comme "extrêmement difficile" par mon programme....

Pour info, la vraie grille initiale porte le nom de code Silver Plate. On la trouve sur http://www.sudoku.com/

J'ai fait un petit programme de sudoku qui les analyse, en fabrique de nouveaux (la difficulté est à choisir) et qui aide à les résoudre.
Si ça interesse quelqu'un, je le donne : le source est en C++ et il fonctionne sous environement windows, mais comme il date un peu, il faut des fois "simuler" du windows un peu ancien. Par contre, je ne sais pas où le mettre pour le donner...

Ca m'intéresse, mais j'ai des questions sur ton programme avant tout. On ouvre un post à un endroit ad hoc pour en parler ?

[fatal_error]

Ca m'intéresse également!

[Ben314]

Ca m'intéresse, mais j'ai des questions sur ton programme avant tout. On ouvre un post à un endroit ad hoc pour en parler ?

Pas de problèmes...