Démonstration par l'absurde : mon avis... et le vôtre ?

[leon1789]

Pour mémoire (je note, je note... :we: ) :

hé l'eau ,
j'ai une question ! :id:


Comme je ne crois pas au hasard dans l'élaboration des preuves mathématiques, il y a bien une explication au fait que cette preuve par l'absurde de P infini soit toujours citée. (c'est même la première dans le "grand livre")

Quand on écrit un truc, j'imagine que soit on y a réfléchi, soit c'est instinctif.

Vous écrivez (regardez-moi bien dans les yeux) cette preuve par l'absurde, ok. Est-ce par instinct ou par choix délibéré (si tel est le cas, quelle en est la raison ?) ?

Merci pour vos éventuelles réponses
(ha ben oui, faut être poli :zen: )

Ben, c'est d'une part par habitude (après avoir vu de nombreux profs faire comme ça), d'autre part par instinct (on a envie pour prouver une existence de remplacer le "il existe" par un "pour tout", donc on absurdise le tout). Mon prof de spé disait souvent : "quand je veux démontrer qu'il existe quelque chose, je suppose que ça n'existe pas et ôlala ça va pas". Ca m'a sûrement marqué...

Euclide c'est pas n'importe qui non plus. Son aura (ses Éléments sont souvent considérés comme le début des maths "axiomatiques") doit y être pour quelque-chose.

Pour moi,les preuves par l absurdes,je les fait par reflexe,mais c est un reflexe délibéré.C est que quand on veut prouver un truc,l absurde permet d obtenir des hypotheses supplémentaires(a savoir que la conclusion est fausse),ce qui peut forcément s avérer utile...

[Black Jack]

La preuve par l'absurde est une technique parmi une multitude d'autres pour résoudre un problème donné.

Ce type de preuve (bien faite) est tout à fait rigoureux, ce n'est pas une demi résolution de problème.

Il n'y a donc aucune raison de se passer de ce type de résolution.

Si plusieurs personnes doivent aller d'une endroit A à un endroit B, la plupart des trajets qu'elles utiliseront seront différents les uns des autres.
Chacun choisit le chemin qui lui semble le meilleur et cependant la plupart des chemins empruntés sont différents.

Pareil pour l'emploi de la preuve par l'absurde, elle en vaut bien une autre si elle permet de résoudre le problème posé... même s'il est possible de s'en passer dans la majorité des cas.

:zen:

[leon1789]

Ce type de preuve (bien faite) est tout à fait rigoureux, ce n'est pas une demi résolution de problème.

Ben disons qu'elle n'apporte tout-à-fait la même "qualité" au résultat ainsi prouvé.

Il n'y a donc aucune raison de se passer de ce type de résolution.

Si plusieurs personnes doivent aller d'une endroit A à un endroit B, la plupart des trajets qu'elles utiliseront seront différents les uns des autres.
Chacun choisit le chemin qui lui semble le meilleur et cependant la plupart des chemins empruntés sont différents.

...et les différences font la richesse, on est d'accord.

Pareil pour l'emploi de la preuve par l'absurde, elle en vaut bien une autre si elle permet de résoudre le problème posé...

En fait, tout dépend ce qu'on appelle "résoudre" ou "réaliser pleinement un énoncé".

Exemple un peu technique (mais pas trop j'espère) :

Soit où les sont des nombres complexes et entiers sur Z (i.e. racine d'un polynôme unitaire de Z[X]). Alors A est un anneau noethérien (i.e. tout idéal de A est engendré par un nombre fini d'éléments).

Maintenant on imagine prendre un exemple d'anneau A, et deux idéaux I = et J= de A. Et bien, malgré la présentation des générateurs de I et de J, muni d'une preuve par l'absurde du résultat ci-dessus, on ne pourra pas exhiber les systèmes générateurs finis des idéaux , de , de , etc.

La preuve ne réalisent donc pas pleinement son résultat. Est-ce satisfaisant ?

EDIT :
Pour exhiber les systèmes générateurs finis des idéaux , de , de , il faut travailler davantage que réaliser une preuve par l'absurde, mais c'est tout a fait possible (puisqu'il y existe des algorithmes)

[ThSQ]

D'un côté tout extension finie d'un Noethérien l'est aussi (avec la grosse artillerie) donc ça règle la question dans le cas général.
D'un autre côté dans des cas concrets on peut (parfois ...) dérouler un algo de construction explicite.

Tout ça me parait complémentaire et pas contradictoire ou antagoniste.

[leon1789]

Tout ça me parait complémentaire et pas contradictoire ou antagoniste.

Que ce soit sur l'exemple des anneaux noethériens, ou plus généralement sur des raisonnements par l'absurde, je n'ai pas d'antagonisme (oui oui, je vous assure !).

Je ne rejette pas le raisonnement par l'absurde (j'en fais aussi au brouillon) mais je trouve que c'est un raisonnement inachevé, qui cache des choses, etc. Oui, commencer un raisonnement par l'absurde, c'est a priori plus simple (et encore, ça dépend des énoncés et des outils utilisés) qu'un raisonnement direct, mais je pense que cette apparente facilité se paie quelque part. Ce que je dis là a l'air très délirant, mais bon...

Hors sujet :
A mon avis, les maths intuitionnistes ne seraient pas aussi développées si les maths classiques n'étaient pas là. Par ailleurs, les maths intuitionnistes soulèvent des résultats plus "précis" que ceux de maths classiques, parce que les outils habituellement utilisés ne sont pas les mêmes. Et comme tout résultat intuitionniste est valable en math classique, on y gagne dans les deux "mondes".
Bref, comme tu dis : Tout ça me parait complémentaire et pas contradictoire ou antagoniste.

[ThSQ]

je pense que cette apparente facilité se paie quelque part. Ce que je dis là a l'air très délirant, mais bon...

Plutôt. Tu peux développer un peu là ?

[Doraki]

leon1789, tu dois bien aimer l'isomorphisme de Curry-Howard.

[leon1789]

Pardon de tarder à répondre... Mais je pense à vous.
(Merci Doraki pour Curry-Howard :id:)

[leon1789]

Pour mémoire :
http://www.maths-forum.com/showthread.php?t=82420&page=1&pp=10

(...) j'ai appris rapidement en donnant des cours particuliers et en voyant les réactions des élèves qu'essayer de leur inculquer de nouvelles méthodes lorsqu'on leur appris toute leur vie étudiante à s'en tenir au minimum et a priori au plus simple, c'est vraiment difficile et on arrive rapidement à perdre l'élève. D'où le fait que je m'en tienne, à contre coeur, à ce genre de résolution.
Ce message aurait sa place aussi dans ton post pour l'absurde, effectivement cette preuve n'apporte pas beaucoup de renseignement bien qu'elle permette d'arriver souvent au but, mais elle a le mérite d'être simple et souvent comprise par la majorité des élèves, à l'opposé des preuves directes souvent trop "recherchées" pour être comprises. Rappelons que l'enseignement ne cherche pas à rendre les élèves bons mais à les rendre moins mauvais...

Amicalement.

[leon1789]

leon1789, tu dois bien aimer l'isomorphisme de Curry-Howard.

Il est certain que, pour moi, le caractère expérimental des maths est assez important, même si je ne suis pas du tout un expert du lambda-calcul.
Mais je ne suis pas sensible uniquement au coté "expérimentable".

Plutôt. Tu peux développer un peu là ?

Il y a des gens (comme moi :briques:) qui n'aiment pas se limiter aux preuves d'existence (sans pour autant en dénigrer l'intérêt !) : on va dire qu'une preuve d'existence, c'est une preuve qui ne donne aucun moyen de réaliser ce qu'elle annonce, bien que le résultat a l'air concretisable.
(je ne parle pas des trucs pas constructifs, cf ensembles non mesurables and co.)

Mais les raisonnements par l'absurde, c'est "pire" que des preuves d'existence : ce sont des preuves d'inexistence !! Doit-on se satisfaire que tel truc imaginaire n'existe pas ... tel autre truc imaginaire n'existe pas ... encore tel truc imaginaire n'existe pas ...
Est-ce que c'est en collectionnant des trucs qui n'existent pas qu'on arrive à converser concrètement dans un forum sur un le net ? :ptdr:

[leon1789]

Pour mémoire :
http://www.maths-forum.com/showthread.php?t=82420&page=1&pp=10

(...) j'ai appris rapidement en donnant des cours particuliers et en voyant les réactions des élèves qu'essayer de leur inculquer de nouvelles méthodes lorsqu'on leur appris toute leur vie étudiante à s'en tenir au minimum et a priori au plus simple, c'est vraiment difficile et on arrive rapidement à perdre l'élève. D'où le fait que je m'en tienne, à contre coeur, à ce genre de résolution.
Ce message aurait sa place aussi dans ton post pour l'absurde, effectivement cette preuve n'apporte pas beaucoup de renseignement bien qu'elle permette d'arriver souvent au but, mais elle a le mérite d'être simple et souvent comprise par la majorité des élèves, à l'opposé des preuves directes souvent trop "recherchées" pour être comprises. Rappelons que l'enseignement ne cherche pas à rendre les élèves bons mais à les rendre moins mauvais...

Amicalement.

Voilà, c'est très bien dit par Nightmare : il y a malheureusement une satisfaction "habituelle" du minimum... et à ce jeu, il est vrai le raisonnement par l'absurde remplit bien son rôle.


Par ailleurs,
je fais peut-être un procès d'intention, mais ne laisse-t-on pas croire aux élèves que seul l'énoncé du théorème compte ? Et que ce qui est raconté par sa preuve est secondaire ? Je veux dire par là, une fois la preuve effectuée et le théorème énoncé, ultérieurement revient-on parfois à l'intérieur de la preuve pour en tirer quelque chose d'autre ? J'ai l'impression que non, et dans ces conditions, il est peut-être difficile d'imaginer pourquoi une preuve par l'absurde n'est pas entièrement satisfaisante.

[leon1789]

Un exemple (petit, très petit...) de ce que je veux dire par retenir le résultat mais aussi les preuves (quand elles le permettent)



Imaginons le texte suivant :

Soit la suite Un définie par et

1} Montrer que Un est (strictement) négative

2} Montrer que Un est décroissante

3} En déduire que Un tend vers -oo

Réponse à 1} :
par récurrence [ alors , donc . Mais d'où contradiction ! Conclusion : pour tout n ,

Une autre réponse à 2} :
"directement" : donc, pour tout n,

Réponse à 3} :
Ici, la manière d'avoir répondu à la question 2} et ce qu'on a retenu de la preuve est important !

En effet, si on a fait un raisonnement par l'absurde dans pour 2}, on sait que Un est décroissante : elle possède donc une limite dans . Il reste à montrer que cette limite est -oo. Peut-être va-t-on le faire encore par l'absurde...

Si on a fait le second raisonnement "direct" dans pour 2} et qu'on ne retient que la conclusion, alors on sait que Un est décroissante : elle possède donc une limite dans . Il reste à montrer que cette limite est -oo... (même situation qu'avant pourrait-on dire)

Mais si on a fait le second raisonnement "direct" dans pour 2} et qu'on relie la preuve, on voit que pour tout n. Il est alors évident que Un tend vers -oo ! A U0, si on retire 5 (ou davantage) une infinité de fois, il ne reste pas grand chose...

Enfin, il est clair que cette possibilité de relecture dans un raisonnement par l'absurde est impossible, puisqu'on ne connait pas la valeur de vérité des assertions établies dans un tel raisonnement. Dans un raisonnement "direct", on sait que tout ce qui est écrit est vrai, donc réutilisable plus tard si nécessaire.

[leon1789]

Discussion de http://maths-forum.com/showthread.php?t=83588&page=2&pp=10

Personnellement j'aime bien le raisonnement par l'absurde car il m'inspire parfois quelques petites idées mais on peut sans aucun doute s'en passer.

Le fait que le raisonnement par l'absurde t'a inspiré ce cheminement logique est indéniable (idem de manière générale dans d'autres situations), et il est important d'avoir des idées. Pas de doute là-dessus.

Mais au final, dans cet exemple, la contradiction disparait toute seule puisque la preuve démontre qu'on obtient un bipoint unicolore (et c'est bien ça la question posée !). C'est un peu comme une récurrence qui n'utilise pas l'hypothèse de récurrence dans la preuve de l'hérédité : dans ce cas, dit-on que c'est une preuve par récurrence ?

ça me rappelle je ne sais plus quel mathématicien qui reprenait toutes les démonstrations faites sur les bases de l'analyse non-standard pour montrer son inutilité

Je ne pense pas que le raisonnement par l'absurde soit inutile, mais plutôt qu'il est bcp trop souvent admis comme "suffisant" (le mot "suffisant" est à prendre dans plusieurs sens, pas uniquement logique). Or c'est un raisonnement "négatif" par essence même puisqu'il dit pourquoi quelque chose est faux. Ce qui est très dommage je pense, c'est que, la plupart du temps, il est simple de dégager quelque chose de "positif" sur la base d'un raisonnement par l'absurde et qu'on ne le fait pas !
Et ce qui m'étonne, c'est que bcp de gens y sont complètement insensibles (je ne parle pas de imod ou ffpower, mais de gens que je croisent ici et là...) à tel point que toutes leurs preuves (ou presque, j'exagère un peu) commencent par "Montrons par l'absurde...".

Imaginons deux GPS qui annonceraient :
GPS_absurde : >
GPS_direct : >
Lequel choisissez-vous ?

[yos]

Montrer que .

(je n'ai pas écrit "" car je n'aime pas être négatif)

[leon1789]

Montrer que .

(je n'ai pas écrit "" car je n'aime pas être négatif)

ok, les deux phrases sont évidemment aussi négatives l'une que l'autre.

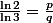
Doit-on "faire croire" qu'il faut partir d'une égalité pour en déduire des trucs dont on ne sait pas s'ils sont faux ou vrais ? (car on se place dans un système contradictoire d'entrée de jeu)

Je préfère largement étudier la différence :
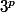
Là, je pense au fait que est pair et impair avec p,q > 0 : , donc , donc pour tout rationnel .

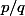
Je sais que vous allez dire que c'est exactement pareil que la preuve par l'absurde (que j'ai remis à l'envers, horreur !)... Mais en fait, ce n'est pas pareil, car après la seconde méthode, on peut aller naturellement un poil plus loin en cherchant un minorant de (et trouver par exemple ). On peut le faire car on sait que cela à un sens, nous ne sommes pas dans un système contradictoire.
Et cela me paraît difficile dans la première méthode (par l'absurde)...


Un peu comme dans http://maths-forum.com/showpost.php?p=531732&postcount=187 , je pense qu'une preuve d'un certain résultat peut avoir un impact sur la question qui vient ensuite. Un raisonnement par l'absurde est "clos" et ne donne rien de plus que le résultat attendu. C'est déjà pas mal, ok (si le résultat attendu est un bon "résumé"), mais à quoi servira ce résultat plus tard ? Sera-t-il alors suffisant ? En tout cas, il sera inutile d'aller chercher du rab dans sa preuve (par l'absurde) pour être plus précis et avoir un complément d'information.
De ce point de vue, une preuve non contradictoire est "ouverte", elle pourra peut-être aider à répondre à la question suivante, on pourra piocher dedans pour tirer un fait qui ne nous avait pas paru a priori important, etc.


Bref, je veux dire que tout ça s'inscrit dans une stratégie "globale", pas du tout "ponctuelle". Retarder les situations contradictoires, c'est augmenter les possibilités de réinvestissement.

[yos]

ok, les deux phrases sont évidemment aussi négatives l'une que l'autre.

Tu sous-entend que R-Q n'est pas un ensemble!?

Doit-on "faire croire" qu'il faut partir d'une égalité pour en déduire des trucs dont on ne sait pas s'ils sont faux ou vrais ? (car on se place dans un système contradictoire d'entrée de jeu)

Serait-ce la première chose que tu as faite? Si oui, tu feras trois paters et deux avés ce soir.

Je sais que vous allez dire que c'est exactement pareil que la preuve par l'absurde (que j'ai remis à l'envers, horreur !)...

Tu m'enlèves les mots de la bouche.

Mais en fait, ce n'est pas pareil, car après la seconde méthode, on peut aller naturellement un poil plus loin en cherchant un minorant de

Avec p et q entiers quelconques, ben voyons. Cherche un truc plus réaliste, tu peux y arriver.

[leon1789]

Tu sous-entend que R-Q n'est pas un ensemble!?

heu nan, j'ai rien sous-entendu de tel... Quel sens donnes-tu à , si ce n'est ?

Serait-ce la première chose que tu as faite? Si oui, tu feras trois paters et deux avés ce soir.

:zen:
Est-ce qu'on est obligé d'écrire ses brouillons dans leur intégralité ?

Tu m'enlèves les mots de la bouche.

ah ben tu vois, j'te connais bien ! :id:

Avec p et q entiers quelconques, ben voyons. Cherche un truc plus réaliste, tu peux y arriver.

Il me semble que le problème de minoration de n'est intéressant que lorsque p/q est proche de , donc il me semble légitime de prendre q > p > 0. Et dans ce cas le minorant (pas génial) que je signale est tout-à-fait réaliste. Et même s'il était faux (je peux me tromper comme tout le monde), cela ne change rien au fait qu'une preuve par l'absurde est "close" par rapport à une preuve non contradictoire. Es-tu d'accord sur ce fait ? Je ne dis pas qu'une preuve par l'absurde ne sert à rien, mais seulement qu'il est bon de voir ce qu'elle cache et qu'on ne peut pas réemployer si on ne le met pas clairement à jour.

[leon1789]

Voici deux énoncés :

R, dérivable, dont le graphe passe par A(0,0) B(1,0) C(2,2) et la tangente en A est horizontale. Montrer que le graphe de f n'est pas une parabole.
>>

Tel quel, je trouve que cet énoncé appelle un raisonnement par l'absurde puisqu'il faut démontrer qu'un truc est faux : on écrit toutes les hypothèses + le fait que f est polynomiale de degré 2 et on constate que c'est contradictoire.

>

Tel quel, cet énoncé fait plutôt appel à des preuves "directes". Et j'ai l'impression qu'il est plus précis (et pas plus difficile à résoudre) que le premier énoncé à cause de sa première question existentielle.

Le problème soulevé est de savoir ce que l'on veut retenir des preuves car, en effet, un théorème n'est qu'un résumé de sa preuve (je pense).

Bref, les énoncés et leurs preuves forment un ensemble cohérent : les preuves par l'absurde servent à montrer des résultats d'inexistence, elles sont adaptées à ce type de théorème.
Mais ne peut-on pas plutôt signaler des théorèmes d'existence ? Et que l'on prouve avec des preuves non contradictoires (puisque dans le "même sens" que les théorèmes) ? Il me semble qu'on y gagne...

[yos]

heu nan, j'ai rien sous-entendu de tel... Quel sens donnes-tu à , si ce n'est ?

La première est négative, pas la seconde (l'ensemble R-Q étant aussi respectable que Q, il n'y a rien de négatif à dire qu'un élément lui appartient). Tout cela pour dire que le côté "négatif" d'une affirmation n'a pas de sens mathématique et que le parallèle avec le GPS ne tient pas trop.

Il me semble que le problème de minoration de n'est intéressant que lorsque p/q est proche de , donc il me semble légitime de prendre q > p > 0. Et dans ce cas le minorant (pas génial) que je signale est tout-à-fait réaliste.

Dans l'autre message tu parlais de minorer et je vois pas qu'on puisse minorer par un truc indépendant de q (mais là je me trompe peut-être). En tout cas ce n'est pas du tout la question qui est posée. L'ouverture que tu proposes est artificielle et repose sur ta culture qui dépasse de loin la question posée.
Mets-toi à la place d'un élève de prépa par exemple à qui cette question est posée. Qu'il soit moyen ou excellent, il fera un raisonnement par l'absurde! Mais qu'il soit moyen ou excellent, il n'ira pas inventer la théorie de l'approximation diophantienne. A ce tarif là toute méthode est fermée.

une preuve par l'absurde est "close" par rapport à une preuve non contradictoire. Es-tu d'accord sur ce fait ?

Ben justement, je suis pas convaincu.

[Nightmare]

Il me semble que Wiles a démontré Fermat par l'absurde, et je crois que sa démonstration est tout sauf "close" à la vue des outils découverts et employés pour la construire.