Démonstration par l'absurde : mon avis... et le vôtre ?
démonstration par l'absurde : mon avis... et le vôtre ?
Bonjour,
Je me suis aperçu que, depuis quelques temps déjà (et de manière inconsciente jusqu'ici !), je n'aime pas les démonstrations par l'absurde. Vous me direz que les goûts ne se discutent pas. Certes, mais là, c'est n'est pas une histoire de goût, mais tout-à-fait mathématique... :hein:
En fait, je ne suis pas choqué par le tiers exclus (que j'utilise sans problème), mais je trouve qu'utiliser un raisonnement par l'absurde, c'est en réalité cacher des choses vraies en montrant des choses plus ou moins fausses ou qui n'existent pas. Vous me direz que le tiers exclus est la source même de la validité d'un raisonnement par l'absurde. Certes, mais je ne remets pas en cause sa validité, mais son utilité réelle... :hein:
Je pense que 99% des démonstrations par l'absurde peuvent être re-rédigées avec les mêmes arguments (donc sans efforts supplémentaires si je peux dire) comme des démonstrations directes, avec en prime de temps à autres une preuve un poil plus simple et/ou un résultat un poil plus fort... :happy2:
Dans les livres, je ne compte plus les preuves par l'absurde qui sont en fait re-rédigeables en démonstrations directes (exemple : infinité des nombres premiers, irrationalité de racine de 2, pas de surjection de E sur P(E), non dénombrabilité des réels, existence et finitude des idéaux minimaux dans les anneaux noethériens, etc.).
Alors pourquoi se satisfait-on des preuves par l'absurde ? Préfère-t-on écrire des preuves contenant des choses plus ou moins fausses (et donc impossibles à réutiliser) que des choses vraies ?
En clair, je pense que le raisonnement par l'absurde devrait être réservé à la recherche sur brouillon, et que la rédaction finale d'une preuve devrait éviter ce raisonnement... On y gagnerait sur plusieurs tableaux ! :we:
Enfin, je suis à la recherche d'un exemple de preuve par l'absurde de A=>B où on utiliserait les hypothèses A et non B au moins deux fois chacune... :happy: Ce serait pour moi une bonne démonstration par l'absurde.
Je me suis aperçu que, depuis quelques temps déjà (et de manière inconsciente jusqu'ici !), je n'aime pas les démonstrations par l'absurde. Vous me direz que les goûts ne se discutent pas. Certes, mais là, c'est n'est pas une histoire de goût, mais tout-à-fait mathématique... :hein:
En fait, je ne suis pas choqué par le tiers exclus (que j'utilise sans problème), mais je trouve qu'utiliser un raisonnement par l'absurde, c'est en réalité cacher des choses vraies en montrant des choses plus ou moins fausses ou qui n'existent pas. Vous me direz que le tiers exclus est la source même de la validité d'un raisonnement par l'absurde. Certes, mais je ne remets pas en cause sa validité, mais son utilité réelle... :hein:
Je pense que 99% des démonstrations par l'absurde peuvent être re-rédigées avec les mêmes arguments (donc sans efforts supplémentaires si je peux dire) comme des démonstrations directes, avec en prime de temps à autres une preuve un poil plus simple et/ou un résultat un poil plus fort... :happy2:
Dans les livres, je ne compte plus les preuves par l'absurde qui sont en fait re-rédigeables en démonstrations directes (exemple : infinité des nombres premiers, irrationalité de racine de 2, pas de surjection de E sur P(E), non dénombrabilité des réels, existence et finitude des idéaux minimaux dans les anneaux noethériens, etc.).
Alors pourquoi se satisfait-on des preuves par l'absurde ? Préfère-t-on écrire des preuves contenant des choses plus ou moins fausses (et donc impossibles à réutiliser) que des choses vraies ?
En clair, je pense que le raisonnement par l'absurde devrait être réservé à la recherche sur brouillon, et que la rédaction finale d'une preuve devrait éviter ce raisonnement... On y gagnerait sur plusieurs tableaux ! :we:
Enfin, je suis à la recherche d'un exemple de preuve par l'absurde de A=>B où on utiliserait les hypothèses A et non B au moins deux fois chacune... :happy: Ce serait pour moi une bonne démonstration par l'absurde.
Salut,
beaucoup de preuves par l'absurde peuvent se faire directement en effet. Mais par exemple l'irrationnalité de racine de deux est quand même très simple par l'absurde. Et il ne faut pas oublier que les mathématiques ce n'est pas de l'informatique, on n'a pas besoin d'avoir de preuves constructives !
beaucoup de preuves par l'absurde peuvent se faire directement en effet. Mais par exemple l'irrationnalité de racine de deux est quand même très simple par l'absurde. Et il ne faut pas oublier que les mathématiques ce n'est pas de l'informatique, on n'a pas besoin d'avoir de preuves constructives !
leon1789 a écrit:Alors pourquoi se satisfait-on des preuves par l'absurde ? Préfère-t-on écrire des preuves contenant des choses plus ou moins fausses (et donc impossibles à réutiliser) que des choses vraies ?
Parce que c'est justement le raisonnement qu'on utilise pour trouver la démonstration, c'est un raisonnement qu'on essaie « naturellement » pour certaines choses et qu'à partir du moment où il n'est pas 10 fois plus compliqué qu'un autre il n'y a pas de raison de vouloir à tout prix faire une démonstration directe ?
Qu'est-ce que tu veux dire par « impossible à réutiliser » ? Ce qui compte dans une démonstration ce sont les techniques employées, et ça c'est souvent réutilisable. Et « contenant des choses plus ou moins fausses » ? Une démonstration par l'absurde démontre des propriétés à partir de certaines hypothèses fixées au départ, le but est de montrer que les hypothèses de départ sont fausses, mais les implications montrées dans la démonstration sont vraies.
Enfin, je suis à la recherche d'un exemple de preuve par l'absurde de A=>B où on utiliserait les hypothèses A et non B au moins deux fois chacune... :happy: Ce serait pour moi une bonne démonstration par l'absurde.
Le nombre de fois où une hypothèse est utilisée dans une démonstration n'est pas un moyen pertinent de mesure de l'utilité de cette hypothèse, on peut trouver des démonstrations où une hypothèse est utilisée à un seul endroit et où il faut faire attention pour remarquer qu'elle est utilisée, et où le résultat devient faux si on supprime cette hypothèse.
Merci de prendre part à la discussion.
Ok, prenons cet exemple.
Preuve par l'absurde. Soit une fraction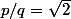 . On commence par réduire la fraction
. On commence par réduire la fraction 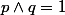 et on écrit
et on écrit 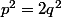 . On voit donc que 2 divise
. On voit donc que 2 divise 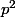 , donc 2 divise
, donc 2 divise  , donc 4 divise
, donc 4 divise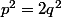 , donc 2 divise
, donc 2 divise 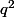 , donc 2 divise
, donc 2 divise  , donc 2 divise
, donc 2 divise 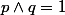 : absurde, donc une telle fraction n'existe pas.
: absurde, donc une telle fraction n'existe pas.
La preuve est très simple (l'argument principal vient de la divisibilité par 2). Je trouve celle-ci au moins aussi simple :
Preuve directe. Tous les entiers non nuls s'écrivent de manière unique comme produit d'un nombre impair et d'une puissance de 2. Soit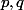 deux entiers non nuls : l'exposant de 2 est pair dans
deux entiers non nuls : l'exposant de 2 est pair dans 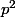 , et impair dans
, et impair dans 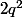 . Donc
. Donc  , donc
, donc 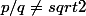 .
.
Bien que je trouve la preuve directe plus nette, on n'y apprend pas vraiment grand chose de plus qu'avec la preuve par l'absurde. Mais il se trouve des exemples où il en va autrement. J'en reparle plus bas.
Je tiens à préciser que pour moi, cela n'a rien à voir avec l'informatique, les maths constructives, etc. J'utilise la contraposée, le tiers exclus, et tout et tout...
Exemple : la preuve (par l'absurde) habituelle de l'infinité des nombres premiers amène en fait un moyen de générer une infinité de nombres premiers quand on la lit dans le sens direct. Bon là, c'est seulement algorithmique, ok.
Autre exemple : dans les quelques livres que j'ai parcourus, le fait que
> (*)
se montre toujours par l'absurde (en considérant un élément maximal d'un ensemble qui se révèlera vide après la démo...). En fait, quand on relit la preuve mais dans le sens direct, avec les mêmes arguments, on voit que l'on démontre naturellement un truc un poil plus fort
>
dont (*) est corollaire. En plus, cela soulève la question : est-ce que cette suite est incluse dans un idéal minimal ?
Ré-écrire dans le sens direct une preuve initialement par l'absurde est un exercice intéressant mathématiquement car cela peut être source de petites simplifications, de nouvelles questions, etc. Non ?
bruce.ml a écrit:Salut,
beaucoup de preuves par l'absurde peuvent se faire directement en effet. Mais par exemple l'irrationnalité de racine de deux est quand même très simple par l'absurde.
Ok, prenons cet exemple.
Preuve par l'absurde. Soit une fraction
La preuve est très simple (l'argument principal vient de la divisibilité par 2). Je trouve celle-ci au moins aussi simple :
Preuve directe. Tous les entiers non nuls s'écrivent de manière unique comme produit d'un nombre impair et d'une puissance de 2. Soit
Bien que je trouve la preuve directe plus nette, on n'y apprend pas vraiment grand chose de plus qu'avec la preuve par l'absurde. Mais il se trouve des exemples où il en va autrement. J'en reparle plus bas.
bruce.ml a écrit: Et il ne faut pas oublier que les mathématiques ce n'est pas de l'informatique, on n'a pas besoin d'avoir de preuves constructives !
Je tiens à préciser que pour moi, cela n'a rien à voir avec l'informatique, les maths constructives, etc. J'utilise la contraposée, le tiers exclus, et tout et tout...
Exemple : la preuve (par l'absurde) habituelle de l'infinité des nombres premiers amène en fait un moyen de générer une infinité de nombres premiers quand on la lit dans le sens direct. Bon là, c'est seulement algorithmique, ok.
Autre exemple : dans les quelques livres que j'ai parcourus, le fait que
> (*)
se montre toujours par l'absurde (en considérant un élément maximal d'un ensemble qui se révèlera vide après la démo...). En fait, quand on relit la preuve mais dans le sens direct, avec les mêmes arguments, on voit que l'on démontre naturellement un truc un poil plus fort
>
dont (*) est corollaire. En plus, cela soulève la question : est-ce que cette suite est incluse dans un idéal minimal ?
Ré-écrire dans le sens direct une preuve initialement par l'absurde est un exercice intéressant mathématiquement car cela peut être source de petites simplifications, de nouvelles questions, etc. Non ?
abcd22 a écrit:Parce que c'est justement le raisonnement qu'on utilise pour trouver la démonstration, c'est un raisonnement qu'on essaie « naturellement » pour certaines choses (...)
oui, dans un premier temps, un raisonnement par l'absurde aide bien : quand on est dans le pétrin, on ne refuse pas l'aide d'un petit raisonnement par l'absurde, c'est certain.
abcd22 a écrit:(...) et qu'à partir du moment où il n'est pas 10 fois plus compliqué qu'un autre il n'y a pas de raison de vouloir à tout prix faire une démonstration directe ?
C'est là où je ne suis pas d'accord : j'ai l'impression qu'on gagne parfois à refaire la preuve dans le sens direct... mais là, c'est complètement expérimental car je n'ai pas de preuve de ça évidemment. :we: Disons que vouloir remettre une démo par l'absurde dans le sens direct (ou contraposé !), c'est une occasion de simplifier la preuve, et parfois ça marche ! :we: C'est par de multiples exemples que je suis arrivé inconsciemment à penser cela.
abcd22 a écrit:Qu'est-ce que tu veux dire par « impossible à réutiliser » ? Ce qui compte dans une démonstration ce sont les techniques employées, et ça c'est souvent réutilisable. Et « contenant des choses plus ou moins fausses » ? Une démonstration par l'absurde démontre des propriétés à partir de certaines hypothèses fixées au départ, le but est de montrer que les hypothèses de départ sont fausses, mais les implications montrées dans la démonstration sont vraies.
Oui, les implications sont correctes, les techniques aussi (comme dans tout raisonnement : par l'absurde ou direct, récurrence, etc.) mais les assertions démontrées dans un raisonnement ne sont pas fiables puisqu'elles aboutissent à une contradiction.
Imaginons démontrer A=>B : on suppose A et non B, et on démontre C1, C2, C3, ... puis une absurdité.
Dans les assertions C1,C2,C3, certaines sont vraies sous l'hypothèse A, d'autres vraies sont l'hypothèse non B, d'autres fausses de manière générale. Mais lesquelles ? On ne le sait pas avec la preuve, sauf si on commence à vouloir remettre les choses dans un sens direct (ou contraposé).
abcd22 a écrit:Le nombre de fois où une hypothèse est utilisée dans une démonstration n'est pas un moyen pertinent de mesure de l'utilité de cette hypothèse, on peut trouver des démonstrations où une hypothèse est utilisée à un seul endroit et où il faut faire attention pour remarquer qu'elle est utilisée, et où le résultat devient faux si on supprime cette hypothèse.
Oui, utiliser toutes les hypothèses et voir où elles sont utiles est sain.
Mais je pensais à autre chose : dans un raisonnement par l'absurde A=>B,
si l'hypothèse non B est utilisée une seule fois, c'est très probablement qu'une preuve directe de A=>B est possible ;
si l'hypothèse A est utilisée une seule fois, c'est très probablement qu'une preuve directe de non B=>non A est possible ;
si les hypothèse A et non B sont utilisées au moins deux fois chacune, alors très probablement on ne pourra pas en déduire une preuve directe.
> (*)
[...]
> (**)
abcd22 a écrit:Euh ça si ce n'est pas une preuve par l'absurde je ne sais pas ce que c'est...
Heu, une preuve par l'absurde de quoi ?
(**) implique (*) par contraposée. Mais (*) n'implique pas (**). Donc (**) est mathématiquement plus forte que (*).
Ce que je voulais dire, c'est que dans la preuve habituelle (par l'absurde) de (*), on ne voit pas du tout (**). En fait, dans la preuve, aucun résultat n'est vrai car toute la preuve repose sur un élément maximal d'un ensemble vide.
La preuve par l'absurde commence comme cela : supposons que (0) ne soit pas produit d'idéaux premiers, alors on considère l'ensemble
En fait, dans la preuve, seul l'argument principal est réutilisable et c'est quand on veut refaire la preuve dans le sens direct qu'on est amené très naturellement à énoncer (**). Et en prime, avec la petite question : est-ce que cette suite se trouve dans un idéal premier minimal ?
Une preuve par contraposée c'est juste un cas particulier de démonstration par l'absurde : on commence par supposer le résultat qu'on veut faux (ici on suppose que (0) n'est pas produit d'idéaux premiers) et on montre que ça implique non(hypothèse de départ), aucune des preuves que tu proposes n'est une démonstration directe du résultat.
abcd22 a écrit:Une preuve par contraposée c'est juste un cas particulier de démonstration par l'absurde : on commence par supposer le résultat qu'on veut faux (ici on suppose que (0) n'est pas produit d'idéaux premiers)
On peut dire aussi qu'une preuve directe A=>B est un cas particulier d'une preuve par l'absurde car on commence par supposer l'hypothèse A vraie. Ok, tout raisonnement peut se remettre sous forme de preuve par l'absurde. On peut dire aussi que tout raisonnement par l'absurde est une preuve directe qu'un système d'assertions {A, non B} est contradictoire... etc.
Ok, logiquement, tous les types de raisonnements se valent, je ne le nie pas.
Mais je pense qu'on ne dénichera rien en procédant ainsi : par exemple, je n'ai jamais vu que mettre une preuve directe ou contraposée sous forme d'un raisonnement par l'absurde apporte une propriété plus forte, ou des idées supplémentaires sur la question.
abcd22 a écrit: aucune des preuves que tu proposes n'est une démonstration directe du résultat.
Pour l'instant je n'ai démontré que l'irrationalité de
Je disais aussi que
-- (**) se prouve de manière directe (je n'ai pas écrit la démo, c'est vrai : il faudrait peut-être que je le fasse pour argumenter) ;
-- (**) est strictement plus forte que (*) ;
-- dans l'hypothèse de (**), la question d'un idéal premier minimal contenant une suite strictement croissante se posait. Alors que la preuve habituelle par l'absurde de (*) ne permet pas de se poser de question (puisque les objets de la preuve n'existent pas en fait)
Est-ce faux ?
leon1789 a écrit:oui, dans un premier temps, un raisonnement par l'absurde aide bien : quand on est dans le pétrin, on ne refuse pas l'aide d'un petit raisonnement par l'absurde, c'est certain.
Oui, mais expérimentalement, tout le monde a été "dans le pétrin" à un moment... Et en particulier ceux qui ont découvert le théorème !
Je pense que c'est (entre autres) pour préserver ce caractère mathématico-historique qu'on présente souvent des preuves par l'absurde alors qu'elles peuvent être obtenues par raisonnement direct.
Cela dit, il est vrai qu'une preuve directe bien tournée est souvent plus jolie qu'une preuve par l'absurde de mon point de vue (un peu comme les raisonnements qui n'utilisent intelligemment pas de récurrence...).
SimonB a écrit:Oui, mais expérimentalement, tout le monde a été "dans le pétrin" à un moment... Et en particulier ceux qui ont découvert le théorème !
Je pense que c'est (entre autres) pour préserver ce caractère mathématico-historique qu'on présente souvent des preuves par l'absurde alors qu'elles peuvent être obtenues par raisonnement direct.
Oui effectivement, cet argument "du comment y arriver quand on n'a pas de modèle" est important. Il faut expliquer comment on est arriver au résultat et cela a peut-être davantage d'importance que la preuve elle-même.
Quand on lit un bouquin de maths (pas d'histoire des maths, mais un cours du supérieur par exemple), est-ce l'auteur tient compte de l'historique ? ou bien vise-t-il la plus grande efficacité des arguments, quitte à perdre un peu en pédagogie ?
Retenir uniquement ce premier jet est-il judicieux ? Je pense que oui et non : on n'écrit pas forcément l'intégralité de ses brouillons quand on rédige au propre, mais on est bien content de garder une trace de la démarche initiale aussi.
Mais bon, je crois que faire le petit effort de mettre une preuve dans un sens direct permet parfois de gagner esthétiquement, mais aussi mathématiquement une cerise.
Un exemple sur la non-surjectivité d'une application de ) :
:
Vous connaissez tous la preuve par l'absurde qui consiste à
supposer que \}) possède un antécédent par
possède un antécédent par  :
:
si = Y) alors
alors
-- si = Y) alors
alors ) : absurde
: absurde
-- si) alors
alors ) : absurde
: absurde
absurde dans tous les cas, donc f n'est pas surjective.
Une preuve directe (toujours avec disjonction de cas, certes) est par exemple celle-ci :
pour tout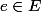 , on a
, on a
-- si) alors
alors 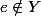 , donc
, donc  \neq Y)
-- si) alors
alors 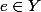 , donc
, donc  \neq Y)
et donc tous les cas \neq Y) .
.
Mais essayons directement de déterminer une partie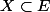 sans antécédent par
sans antécédent par  .
.
Soit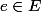 . Avoir
. Avoir  \neq X) , c'est simplement avoir un élément
, c'est simplement avoir un élément 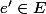 tel que
tel que
[) et
et 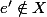 ] ou [
] ou [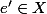 et
et ) ]
] )
Cet élément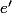 dépend de
dépend de  ... on pourrait l'écrire
... on pourrait l'écrire ) !
!
Maintenant, avec une application injective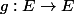 , on prouve que l'ensemble
, on prouve que l'ensemble  \ | \ x \in E \ et \ g(x) \notin f(x) \}) satisfaisait (@) avec
satisfaisait (@) avec ) : en effet,
: en effet,  \in X_g \Leftrightarrow g(x) \notin f(x)) (car g est injective).
(car g est injective).
Donc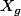 n'a pas d'antécédent par
n'a pas d'antécédent par  .
.
On trouve donc une "tripotée" de parties sans antécédent et en particulier l'ensemble habituel \}) en prenant
en prenant 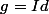 .
.
Enfin, remarquer que (@) apparait dans la preuve directe : c'est d'ailleurs la preuve directe qui m'a amené à la détermination des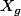 . C'est la cerise...
. C'est la cerise...
Est-ce un peu convaincant ?
Vous connaissez tous la preuve par l'absurde qui consiste à
supposer que
si
-- si
-- si
absurde dans tous les cas, donc f n'est pas surjective.
Une preuve directe (toujours avec disjonction de cas, certes) est par exemple celle-ci :
pour tout
-- si
-- si
et donc tous les cas
Mais essayons directement de déterminer une partie
Soit
[
Cet élément
Maintenant, avec une application injective
Donc
On trouve donc une "tripotée" de parties sans antécédent et en particulier l'ensemble habituel
Enfin, remarquer que (@) apparait dans la preuve directe : c'est d'ailleurs la preuve directe qui m'a amené à la détermination des
Est-ce un peu convaincant ?
leon1789 a écrit:Preuve directe. Tous les entiers non nuls s'écrivent de manière unique comme produit d'un nombre impair et d'une puissance de 2. Soitdeux entiers non nuls : l'exposant de 2 est pair dans
, et impair dans
. Donc
, donc
.
Bonjour.
Sous prétexte de re-rédaction sous une forme directe, tu utilises un résultat beaucoup plus compliqué : l'unicité de la décomposition en facteurs premiers.
De façon générale, c'est bien de se poser ce genre de question d'ordre esthétique et d'ailleurs mon prof de math de 4ème a dit un jour "une belle démonstration est une démonstration directe et pas par l'absurde". C'était il y a près de 30 ans et je me surprends parfois à en tenir compte encore aujourd'hui.
C'est une erreur en tout cas de se focaliser là-dessus : une preuve par l'absurde est souvent plus claire. Tout dépend du contexte.
leon1789 a écrit:Exemple : la preuve (par l'absurde) habituelle de l'infinité des nombres premiers amène en fait un moyen de générer une infinité de nombres premiers quand on la lit dans le sens direct. Bon là, c'est seulement algorithmique, ok.
Pas vraiment : directe ou pas elle ne donne pas de nombre premier supplémentaire explicite. C'est pareil.
SimonB a écrit:(un peu comme les raisonnements qui n'utilisent intelligemment pas de récurrence...).
Exemple?
yos a écrit:Bonjour.
Sous prétexte de re-rédaction sous une forme directe, tu utilises un résultat beaucoup plus compliqué : l'unicité de la décomposition en facteurs premiers.
Je trouve intéressant d'analyser le contenu des preuves : c'est en particulier pour cela que je ne crois pas que rédiger une preuve directe ou par l'absurde est la même chose.
Effectivement, pour faire une preuve directe en s'inspirant d'une preuve par l'absurde, on est parfois amené à utiliser un argument non prévu : d'après mon expérience, si tel est le cas, alors la preuve directe va démontrer un résultat plus fort que celui obtenu avec la preuve par l'absurde. C'est assez "moral", mais un exemple ne ferait pas de mal...
Cela dit, pour cette démo de l'irrationalité de
L'argument principal de la preuve par l'absurde est basé également sur la divisibilité par 2, mais il est vrai qu'il est un poil plus simple dans la preuve par l'absurde.
En revanche, dans la preuve par l'absurde, on a besoin de pgcd, notion certes simple, mais inutilisée dans la preuve directe.
Alors, autant la valution en un premier (nombre ou idéal) est une notion très générale (valable dans tout anneau noethérien par exemple), autant la notion de pgcd est très spéciale (valable dans des anneaux spécifiques, genre anneaux factoriels ou de Dedekind).
En fait, on pourrait se passer de pgcd dans la preuve par l'absurde, mais on parlerait alors de valuation en 2 des entiers p et q...
yos a écrit:De façon générale, c'est bien de se poser ce genre de question d'ordre esthétique et d'ailleurs mon prof de math de 4ème a dit un jour "une belle démonstration est une démonstration directe et pas par l'absurde". C'était il y a près de 30 ans et je me surprends parfois à en tenir compte encore aujourd'hui.
C'est une erreur en tout cas de se focaliser là-dessus : une preuve par l'absurde est souvent plus claire. Tout dépend du contexte.
L'esthétique est une affaire de goût personnel... et là, tout est permis évidemment.
En revanche, je ne suis pas certain que se focaliser sur essayer de rédiger une preuve directe soit une erreur, car ceci est source de questions, de travail et donc d'une meilleure compréhension. Mais ce n'est pas sur les petits exemples habituels que cela se voit... D'ailleurs, je ne m'en suis pas aperçu d'un coup, mais avec le temps...
Je peux oser demander un exemple de preuve par l'absurde ? (histoire de me donner une chance. :happy2: )
yos a écrit:directe ou pas elle ne donne pas de nombre premier supplémentaire explicite. C'est pareil.
> ne caractérise pas un nombre premier ? (C'est pas vraiment génial, certes.) Mais bon, je vois mal comment donner une valeur précise à ce nouveau premier :hein:
yos a écrit:Exemple?
Je crois que SimonB pensait à des résultats que l'on peut prouver par récurrence mais aussi de manière directe. Mais là, il faut vraiment changer les arguments de la preuve (je pense).
leon1789 a écrit:Cela dit, pour cette démo de l'irrationalité de, on n'utilise pas la décomposition en facteurs premiers : nul besoin de factoriser totalement 8008 pour l'écrire
On étudie uniquement la divisibilité par 2 : on pourrait dire (entre nous) la valuation en 2.
L'existence des fonctions valuations repose sur la décomposition en facteurs premiers.
yos a écrit:L'existence des fonctions valuations repose sur la décomposition en facteurs premiers.
Non, pas du tout, et je dirais même que c'est le contraire : nul besoin de factoriser un entier impair pour voir qu'il n'est pas multiple de 2 !
Soit v la fonction qui à un entier N lui fait correspondre le grand exposant k de 2 tel que
v(x) =
v(xy) = v(x) + v(y)
v(x + y)
En revanche, factoriser un entier N en produit de premiers, c'est considéré toutes ses valuations sur les nombres premiers, montrer que cette famille est presque nulle, et prouver l'égalité
Un exemple où la preuve directe montre une généralisation possible d'un résultat obtenu préalablement par l'absurde :
http://www.maths-forum.com/showthread.php?p=317463#post317463
Qu'en pensez-vous ?
http://www.maths-forum.com/showthread.php?p=317463#post317463
Qu'en pensez-vous ?
yos a écrit:Oui tu as raison. C'est parce qu'on dit souvent
"v_p(2)=exposant de 2 dans la DFP"
que j'ai dit ça.
Oui, effectivement, c'est vrai que l'on dit souvent ça pour se faire comprendre rapidement.
Mais c'est peut-être un effet pervers (de l'enseignement) : utiliser les outils très bien connus, même s'ils sont trop forts, le principal étant de faire le cours avec le minimum d'outils et de temps autorisés... On en arrive ainsi à mettre la charrue avant les boeufs, mais ça, vous le savez bien :we:
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
