Démonstration par l'absurde : mon avis... et le vôtre ?

[leon1789]

la demonstration par l absurde est un lieu privilegié du donc tandis que dans le sens direct c est plutot le car

Amusant.
Je dirais : la démonstration par l'absurde a pour but de déboucher sur une impasse logique (et en déduire qu'une hypothèse est fausse), alors que le sens direct a pour but d'expliquer pourquoi une conclusion est vraie.

(celui qui fait du direct donc est censé atteidre sa cible, ce qui est plus dure que lorsque que la cible est n importe quelle contradiction)
c est donc pour un débutant comme moi un outil pratique et assez beau...
puisqu on dit des choses vraies(implications) à propos de choses(hypotheses) fausses.

je d'accord, à l'exception que la dernière pharse : dans une preuve par l'absurde, on ne dit rien de "vrai" a priori. On ne fait que des déductions logiques à partir d'hypothèses (qui finalement se révèlent contradictoires).

mais la dem par l absurde a pour le débutant une facheuse tendance à lui faire croire qu il a montré quelque chose alors qu il s est juste trompé...

oui, tout à fait : c'est un raisonnement avec un double "tranchant", puisqu'il fait disparaître le "garde fou" de la cohérence.

[leon1789]

pour continuer la discussion sur l'absurde je dirais que parfois dans un raisonnement par l'absurde on voit mieux "où on veut en venir" que par un homologue direct quand il existe, non ?

Le raisonnement par l'absurde (comme une récurrence, etc.) est un outil pratique pour trouver une démonstration. C'est pour cela que j'en fais aussi au brouillon.

Mais est-ce que ceci permet de mieux voir les choses ? Est-ce qu'un raisonnement par l'absurde est si naturel que ça ? (ici, je ne parle pas de contraposée)

Pour moi, bien voir où on veut en venir commence par poser la bonne question, qui permettra une bonne réponse. Assez souvent, une "mauvaise" formulation du problème impose plus ou moins une contorsion dans la preuve.

[ffpower]

Oula, c'est de la logique... et je ne suis pas logicien :triste:

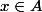
Quelle est la définition "positive" de l'ensemble vide ? Dire que c'est l'ensemble qui ne contient aucun élément, est une définition "négative". Une définition "positive" est peut-être justement la phrase que tu donnes ! => faux
Mais il faudrait poser la question à un logicien.

L ensemble vide serait donc par définition un ensemble "absurde" lol

[Sve@r]

L ensemble vide serait donc par définition un ensemble "absurde" lol

Ben à l'origine de la géométrie (de Pythagore à Euclide), il y a notre environnement et la constatation que l'on peut modéliser le monde dans lequel nous vivons par un espace où chaque objet est décrit par un point ou un ensemble de points. Le concept d'espace a été précédé par celui, plus simple, d'emplacement d'un objet. L'idée d'espace est venue lorsqu'on s'est posé la question de savoir si "l'emplacement" existait indépendamment du fait qu'un objet y soit situé ou non. De là on arrive à l'ensemble vide qui "ne contient aucun objet"...

[ThSQ]

Quelle est la définition "positive" de l'ensemble vide

Soit X un ensemble.



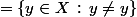
on montre ensuite que cette définition ne dépend pas de X et donc unicité.

[leon1789]

Soit X un ensemble.

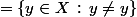
on montre ensuite que cette définition ne dépend pas de X et donc unicité.

oui, c'est ce que je viens justement de voir sur wikipédia :we: merci

L ensemble vide serait donc par définition un ensemble "absurde" lol

oui en quelque sorte :we:

supposons qu on a un ensemble A,et qu on montre disons

et on en déduit
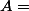
A t on fait un raisonnement par l absurde?

Ben non, c'est la définition d'un ensemble vide :
implique

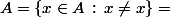
[ffpower]

Bon alors continuons^^.Supposons que je veux montrer une propriété P(x).Je dit soit A l ensemble des x tels que P(x) n est pas vérifiée.Je vérifie qu on a:
x dans A implique x different de x
J en deduis A=ensemble vide et j en deduis donc que P(x) est verifiee pour tout x.Y a t il un raisonnement par l absurde ici lol?

[leon1789]

Bon alors continuons^^.Supposons que je veux montrer une propriété P(x).Je dit soit A l ensemble des x tels que P(x) n est pas vérifiée.Je vérifie qu on a:
x dans A implique x different de x
J en deduis A=ensemble vide et j en deduis donc que P(x) est verifiee pour tout x.Y a t il un raisonnement par l absurde ici lol?

Non, mais il y a clairement un tiers exclus.

[leon1789]

Bon alors continuons^^.Supposons que je veux montrer une propriété P(x).Je dit soit A l ensemble des x tels que P(x) n est pas vérifiée.Je vérifie qu on a:
x dans A implique x different de x
J en deduis A=ensemble vide et j en deduis donc que P(x) est verifiee pour tout x.Y a t il un raisonnement par l absurde ici lol?

Non, mais il y a clairement un tiers exclus.

[Euler911]

Non, mais il y a clairement un tiers exclus.

Quoi, tu vas enchainer sur le tiers exclus??? L'absurde ne te suffit donc pas? Tu sais, on peut soigner tout ça :triste: :ptdr:

[ffpower]

mdrrr :ptdr:
L infini,c'est autorisé?

[leon1789]

Bon alors continuons^^.Supposons que je veux montrer une propriété P(x).Je dit soit A l ensemble des x tels que P(x) n est pas vérifiée.Je vérifie qu on a:
x dans A implique x different de x
J en deduis A=ensemble vide et j en deduis donc que P(x) est verifiee pour tout x.Y a t il un raisonnement par l absurde ici lol?

Tu veux dire par là que, quitte a utiliser le tiers exclus au final, on peut déguiser tout raisonnement par l'absurde en considérant l'ensemble A formé par les x tels que...
Oui, c'est vrai.

[leon1789]

mdrrr :ptdr:
L infini,c'est autorisé?

Heu, tu te trompes de discussion, non ? :id:

Les ensembles infinis, on en parlait pour faire la différence entre un truc concret et un truc imaginaire. Le jour où un ensemble infini sera concret(isé) dans son "ensemble", on sera dans un autre univers. :ptdr:
Cela n'a rien à voir le raisonnement par l'absurde.

[ffpower]

C est effectivement la que je voulais en venir.La methode la n est peut etre pas encore la solution ultime pour virer l absurde,mais c une piste.Mais n empeche que dans ton tout 1er post,tu dis que tu t autorises le tiers exclu^^

[Euler911]

Heu, tu te trompes de discussion, non ? :id:

Les ensembles infinis, on en parlait pour faire la différence entre un truc concret et un truc imaginaire. Le jour où un ensemble infini sera concret(isé) dans son "ensemble", on sera dans un autre univers. :ptdr:
Cela n'a rien à voir le raisonnement par l'absurde.

J'ai rien compris :look2:

[leon1789]

J'ai rien compris :look2:

:zen: Ca vient de cette page
http://maths-forum.com/showthread.php?t=73594&page=2&pp=10

[Euler911]

Je pense (mais je ne suis pas sûr) que j'ai encore moins compris les choses... :look2: :marteau:

[leon1789]

C est effectivement la que je voulais en venir.La methode la n est peut etre pas encore la solution ultime pour virer l absurde,mais c une piste.Mais n empeche que dans ton tout 1er post,tu dis que tu t autorises le tiers exclu^^

Oui, d'un point de vue logique, je suis en pleine contradiction, je le sais bien.

Les écoles intuitionnistes ou constructivistes, elles, refusent catégoriquement le tiers exclus. Il ne faut pas croire que cela ne mène mathématiquement à rien. Au contraire, cela donne naissance à des outils qu'on n'a pas l'habitude d'utiliser en maths classiques.

Mais je ne suis pas un extrémiste ! :ptdr: C'est simplement que je pense que le raisonnement par l'absurde est un raisonnement "inachevé"... et que trop souvent, on s'en contente :hum:

[leon1789]

Bon alors continuons^^.Supposons que je veux montrer une propriété P(x).Je dit soit A l ensemble des x tels que P(x) n est pas vérifiée.Je vérifie qu on a:
x dans A implique x different de x
J en deduis A=ensemble vide et j en deduis donc que P(x) est verifiee pour tout x.Y a t il un raisonnement par l absurde ici lol?

ok.

Montrons que P(x) => Q(x) . Soit A = { x | P(x) et non Q(x) }
On mouline un peu et on montre que A est vide, ce qui permet de conclure.

Mais est-ce intéressant d'analyser l'ensemble vide ?
N'est-il pas plus intéressant d'analyser { x | P(x) } et/ou { x | non Q(x) } ?

[leon1789]

Bon alors continuons^^.Supposons que je veux montrer une propriété P(x).Je dit soit A l ensemble des x tels que P(x) n est pas vérifiée.Je vérifie qu on a:
x dans A implique x different de x
J en deduis A=ensemble vide et j en deduis donc que P(x) est verifiee pour tout x.Y a t il un raisonnement par l absurde ici lol?

ok.

Montrons que P(x) => Q(x) . Soit A = { x | P(x) et non Q(x) }
On mouline un peu et on montre que A est vide, ce qui permet de conclure.

Mais est-ce intéressant d'analyser l'ensemble vide ?
N'est-il pas plus intéressant d'analyser { x | P(x) } et/ou { x | non Q(x) } ?

Exemple http://www.maths-forum.com/showthread.php?t=76031&page=1&pp=10

Bonjour , voici un petit exo :
Soient deux à deux distincts, soit .
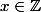
Montrer que si alors pour tout , est différent de 3.
Et montrer de même qu'on ne peut pas avoir .

Pourquoi vouloir montrer que des choses n'existent pas... N'est-il pas plus intéressant (en tout cas plus fort mathématiquement) de prendre moins d'hypothèses (i.e. en écrire moins !) et d'en déduire des choses ? Par exemple

Bonjour , voici un petit exo :
Soient et .
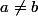
Montrer que si et alors P ne peut atteindre 3 qu'en (a+b)/2.
Et montrer de même que implique a=b=c

Est-ce que ce deuxième énoncé ne vous parait pas plus intéressant que de parler de l'ensemble vide ? :id: