On prend E l'ensemble des suites à valeurs complexes et on définit l'opérateur T : E dans E qui à u associe la suite ((n+1)u_{n+1}).
Ma première question : est -ce que je peux considérer que T est un endomorphisme?
Quand je regarde la définition d'un opérateur, on dit que c'est une application entre deux espaces vectoriels qui est linéaire sur son ensemble de définition.
Je ne vois aucune différence avec la définition d'un endomorphisme.
Merci d'avance pour vos réponses.
Opérateur? endomorphisme?
6 messages
- Page 1 sur 1
Re: opérateur? endomorphisme?
Bonjour
C'est une histoire de vocabulaire. Pour moi "endomorphisme", c'est plutôt utilisé en dimension finie. C'est une application linéaire d'un e.v E vers lui même. Mais si E est de dim infinie je pense qu'on peut le dire aussi (en tout cas cela ne me gêne pas).
Il me semble que opérateur (sous-entendu linéaire) est plus utilisé en dimension infinie.
Mais attention un opérateur va d'un e.v E vers un ev F (F non nécessairement égal à E).
Un opérateur et un endomorphisme ce n'est quand même pas la même chose!!
Remarque: Souvent pour les opérateurs, les espaces E et F sont munis, d'une norme d'une métrique voire d'une topologie. Pour ton exemple c'est quoi la norme sur E ou la topologie?
C'est une histoire de vocabulaire. Pour moi "endomorphisme", c'est plutôt utilisé en dimension finie. C'est une application linéaire d'un e.v E vers lui même. Mais si E est de dim infinie je pense qu'on peut le dire aussi (en tout cas cela ne me gêne pas).
Il me semble que opérateur (sous-entendu linéaire) est plus utilisé en dimension infinie.
Mais attention un opérateur va d'un e.v E vers un ev F (F non nécessairement égal à E).
Un opérateur et un endomorphisme ce n'est quand même pas la même chose!!
Remarque: Souvent pour les opérateurs, les espaces E et F sont munis, d'une norme d'une métrique voire d'une topologie. Pour ton exemple c'est quoi la norme sur E ou la topologie?
Re: opérateur? endomorphisme?
D'accord merci pour l'explication, je pense que la norme ici c'est la valeur absolue.
J'ai plein d'autre question pour cette exercice que j'ai essayé de résoudre, voici les questions :
1)Déterminer les éléments propres de T?
2)Pour a dans C, déterminer Ker(T-aid)^2.
3)Soit V un sous-espace de E de dimension finie et stable par T et u dans V. Montrer que la série de terme général u_n est absolument convergente.
1).pour la valeur propre 0, on a KerT=Vect((1,0,0,...,0,...)). OK
.pour a valeur propre différent de 0, Ker(T-aid)={ens des suites proportionnelle à (a^n/n!)} OK
Ma première question est quel est le spectre de T ? pourquoi dim(Ker(T-aid))=1?
J'ai plein d'autre question pour cette exercice que j'ai essayé de résoudre, voici les questions :
1)Déterminer les éléments propres de T?
2)Pour a dans C, déterminer Ker(T-aid)^2.
3)Soit V un sous-espace de E de dimension finie et stable par T et u dans V. Montrer que la série de terme général u_n est absolument convergente.
1).pour la valeur propre 0, on a KerT=Vect((1,0,0,...,0,...)). OK
.pour a valeur propre différent de 0, Ker(T-aid)={ens des suites proportionnelle à (a^n/n!)} OK
Ma première question est quel est le spectre de T ? pourquoi dim(Ker(T-aid))=1?
Re: opérateur? endomorphisme?
Bonjour
Bon on a l'impression qu'il n'y a pas de norme dans ton exo.
Ceci étant dit
1. Que peux vouloir dire valeur absolue d'une suite? Encore que cela peut se définir mais en quoi serait-ce une norme?
2. Pour faire l'exercice il faut d'abord que l'énoncé soit clair. Ce qui n'est pas le cas. T c'est quoi exactement? si u=(u_0,u_1,....) et v=T u= (v_0,v_1, ....,v_n...)
on a v_n=(n+1)u_{n+1} pour tout n? c'est ça?
De toute façon l'énoncé tu l'as eu quelque part, tu ne pourrais pas le restituer exactement?
Bon on a l'impression qu'il n'y a pas de norme dans ton exo.
Ceci étant dit
1. Que peux vouloir dire valeur absolue d'une suite? Encore que cela peut se définir mais en quoi serait-ce une norme?
2. Pour faire l'exercice il faut d'abord que l'énoncé soit clair. Ce qui n'est pas le cas. T c'est quoi exactement? si u=(u_0,u_1,....) et v=T u= (v_0,v_1, ....,v_n...)
on a v_n=(n+1)u_{n+1} pour tout n? c'est ça?
De toute façon l'énoncé tu l'as eu quelque part, tu ne pourrais pas le restituer exactement?
Re: opérateur? endomorphisme?
Je pense que la norme ne va pas servir pour l'exercice...
Ici T((un))=(n+1)u_{n+1} pour tout n
Re: opérateur? endomorphisme?
Oui c'est ce que je pensais pour T mais je voulais en être sûr.
quelques indications
Pour le 1. il faut revenir à la définition: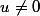 est vecteur propre de valeur propre z pour T si Tu=z u , i.e
est vecteur propre de valeur propre z pour T si Tu=z u , i.e u_{n+1}= z u_n \forall n\in \N) .
.
On peut supposer que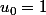 et donc calculer
et donc calculer  en fonction de n avec une simple récurrence...C'est facile à faire donc tu dois trouver toutes les valeurs propres z et les vecteurs propres associés.
en fonction de n avec une simple récurrence...C'est facile à faire donc tu dois trouver toutes les valeurs propres z et les vecteurs propres associés.
Pour le 2. v est ds^2) ssi
ssi (T-zI)v=0) .
.
On a déjà les éléments de) qui sont solutions.
qui sont solutions.
Cherchons les éléments qui ne sont pas ds Ker(T-zI). Posons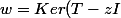v) (
(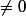.)
Donc (T-zI) w=0, i.e w est un vecteur propre , il restera à résoudre l'équation
w=(T-zI)v pour finir. Encore une fois faire un récurrence.
Normalement on doit obtenir un sev de dim=2 pour^2)
Pour le 3. (indication à vérifier) la question 2 laisse penser que l'opérateur (T-zI) n'est pas nilpotent.
Cela implique que si u n'est pas un vecteur propre mais est dans un espace^n,)
 alors u ne peut être dans V.
alors u ne peut être dans V.
La restriction de T à l'espace V est donc diagonalisable. Comme la série associée à chaque vecteur propre de T est absolument convergente il en sera de même pour tout v dans V puisque v est une c.l finie de vecteurs propres.
quelques indications
Pour le 1. il faut revenir à la définition:
On peut supposer que
Pour le 2. v est ds
On a déjà les éléments de
Cherchons les éléments qui ne sont pas ds Ker(T-zI). Posons
Donc (T-zI) w=0, i.e w est un vecteur propre , il restera à résoudre l'équation
w=(T-zI)v pour finir. Encore une fois faire un récurrence.
Normalement on doit obtenir un sev de dim=2 pour
Pour le 3. (indication à vérifier) la question 2 laisse penser que l'opérateur (T-zI) n'est pas nilpotent.
Cela implique que si u n'est pas un vecteur propre mais est dans un espace
La restriction de T à l'espace V est donc diagonalisable. Comme la série associée à chaque vecteur propre de T est absolument convergente il en sera de même pour tout v dans V puisque v est une c.l finie de vecteurs propres.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
