Inverse d'un opérateur différentiel linéaire

[barbu23]

SLA :
Pour montrer que ; , il suffit de montrer que : pour tout : , non ?

[barbu23]

@SLA :
Pour montrer que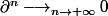
Il faut montrer que :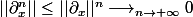 , c'est à dire, il faut montrer que : 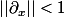, non ?

Edit : Parc que ici : http://en.wikipedia.org/wiki/Neumann_series , ils disent que :
, et donc, il faut montrer que : 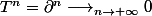, non ?

Edit :
SLA :
Pour montrer que ;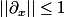 , il suffit de montrer que : 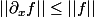pour tout : , non ?

[SLA]

@SLA :
Pour montrer que
Il faut montrer que : , c'est à dire, il faut montrer que : , non ?

Edit : Parc que ici : http://en.wikipedia.org/wiki/Neumann_series , ils disent que :
, et donc, il faut montrer que : , non ?

Edit :
SLA :
Pour montrer que ; , il suffit de montrer que : pour tout : , non ?

On en revient donc à: quelle norme utilises-tu?

Édit:encore plus simple! Ne connais-tu pas une fonction égale à sa dérivée?

[barbu23]

On en revient donc à: quelle norme utilises-tu?

Édit:encore plus simple! Ne connais-tu pas une fonction égale à sa dérivée?

Norme de convergence uniforme, par exemple, ça marche ?
Je cherche une norme qui permet qu'on ait : pour tout ou pour tout . ça existe ?

[barbu23]

Édit:encore plus simple! Ne connais-tu pas une fonction égale à sa dérivée?

la fonction exponentielle, mais à quoi sert -elle ?
Elle sert comme contre-exemple ? Je suis triste d'apprendre ça. :triste:

[barbu23]

Pour quelle classe de fonctions cet opérateur admet un inverse alors ?
Merci d'avance.

[SLA]

Norme de convergence uniforme, par exemple, ça marche ?
Je cherche une norme qui permet qu'on ait : pour tout ou pour tout . ça existe ?

Pour cette norme, ton espace n'est pas complet.

[SLA]

la fonction exponentielle, mais à quoi sert -elle ?
Elle sert comme contre-exemple ? Je suis triste d'apprendre ça. :triste:

Ben si peux tu avoir ?

Enfin, as-tu prouvé que cet opérateur est bien bijectif? Je signale que c'était ma première piste, tu as voulu t'aventurer sur le terrain des séries de Neumann.

[barbu23]

Pour cette norme, ton espace n'est pas complet.

Si on prend par exemple au lieu de , l'espace : avec : un compact ?
Cela se trouve ici : http://www.les-mathematiques.net/a/e/t/node5.php
Donc, dans ce cas là, l'opérateur en question admet un inverse ?

[SLA]

Si on prend par exemple au lieu de , l'espace : avec : un compact ?
Cela se trouve ici : http://www.les-mathematiques.net/a/e/t/node5.php

Non plus. La fonction exponentielle te montre de toutes façons que tu n'as aucune chance de rendre ta série absolument convergente...
As-tu regardé si ton application est bijective?

[barbu23]

As-tu regardé si ton application est bijective?

C'est à dire, je montre que : est bijective dans l'espace des opérateurs linéaires ?

[SLA]

C'est à dire, je montre que : est bijective dans l'espace des opérateurs linéaires ?

Exactement. Regarde l'injectivité puis la surjectivité.

[barbu23]

Non plus. La fonction exponentielle te montre de toutes façons que tu n'as aucune chance de rendre ta série absolument convergente...

Et si je considère la distribution : , la série peut - elle converger au sens des distributions ? ou au sens des espaces ?
Merci d'avance.

[barbu23]

Exactement. Regarde l'injectivité puis la surjectivité.

Donc, on considère l'application : dans l'espace des opérateurs linéaires.
- est injective. En effet :
Soient deux opérateurs linéaires, tels que : , cela signifie que : , c'est à dire : , d'où l'injectivité.
- est surjective. En effet :
Soit un opérateur linéaire. Pour montrer la surjectivité, il suffit de trouver au moins un opérateur linéaire tel que : .
Il suffit de prendre par exemple : . En effet : .
D'où la surjectivité.
est donc bijective, cela signifie qu'on peut trouver son inverse, non ? Quelle est son inverse ?
Est ce que c'est correcte ce que j'ai écrit ?

Merci d'avance.

[SLA]

Et si je considère la distribution : , la série peut - elle converger au sens des distributions ? ou au sens des espaces ?
Merci d'avance.

Non, bah écoute. Prends ta définition de suites convergentes de distributions et regarde si ça marche. Comment veux tu qu'un truc tende vers 0 quand il y a toujours un point qui ne tends pas vers 0.

Bref, tu persistes a vouloir rendre vrai un truc manifestement faux, un L1 peut s'en rendre compte.
Bon courage

[barbu23]

D'accord, merci. Tu peux m donner la réponse à la question qui se trouve ici :

Donc, on considère l'application : dans l'espace des opérateurs linéaires.
- est injective. En effet :
Soient deux opérateurs linéaires, tels que : , cela signifie que : , c'est à dire : , d'où l'injectivité.
- est surjective. En effet :
Soit un opérateur linéaire. Pour montrer la surjectivité, il suffit de trouver au moins un opérateur linéaire tel que : .
Il suffit de prendre par exemple : . En effet : .
D'où la surjectivité.
est donc bijective, cela signifie qu'on peut trouver son inverse, non ? Quelle est son inverse ?
Est ce que c'est correcte ce que j'ai écrit ?

Merci d'avance.

[SLA]

Donc, on considère l'application : dans l'espace des opérateurs linéaires.
- est injective. En effet :
Soient deux opérateurs linéaires, tels que : , cela signifie que : , c'est à dire : , d'où l'injectivité.
- est surjective. En effet :
Soit un opérateur linéaire. Pour montrer la surjectivité, il suffit de trouver au moins un opérateur linéaire tel que : .
Il suffit de prendre par exemple : . En effet : .
D'où la surjectivité.
est donc bijective, cela signifie qu'on peut trouver son inverse, non ? Quelle est son inverse ?
Est ce que c'est correcte ce que j'ai écrit ?

Merci d'avance.

Mets ça de côté pour ce soir. Tu verras mieux demain...
Quel opérateur cherches-tu a inverser?

EDIT: pour le coup, ce que tu écris est un résultat vrai (j'ai pas regardé la preuve) mais ce n'est pas ta question, alors bon...

[barbu23]

Merci beaucoup pour le temps que tu as passé à m'expliquer. :happy3:
Cordialement. :happy3:

[barbu23]

Mets ça de côté pour ce soir. Tu verras mieux demain...
Quel opérateur cherches-tu a inverser?

On cherche, à inverser l'opérateur : qui est une application linéaire, donc, on fait comme en algèbre linéaire, on montre l'injectivité et la surjectivité de l'opérateur :

Il est claire que cet opérateur est surjective, par contre il n'est pas injective, parce que le noyau de cet opérateur, contient une infinité d’éléments, donc, il n'est pas bijective, non ?
Merci d'avance.

[SLA]

On cherche, à inverser l'opérateur : qui est une application linéaire, donc, on fait comme en algèbre linéaire, on montre l'injectivité et la surjectivité de l'opérateur :

Il est claire que cet opérateur est surjective, par contre il n'est pas injective, parce que le noyau de cet opérateur, contient une infinité d’éléments, donc, il n'est pas bijective, non ?
Merci d'avance.

Salut,
Étant donné la tournure que tu as donnée a cette discussion, il va me falloir un peu plus que du "il est clair que".
Peux tu nous expliquer ce que tu viens d'avancer? En particulier, peux tu nous donner cet infinité d'éléments qui constituent le noyau?