Operateur adjoint !

par **barbu23** » 26 Fév 2009, 22:41

Bonsoir :
Pouvez vous de me donner un exemple d'application de la définition de l'adjoint d'un operateur .. comment on le calcule ?
Est ce que la definition s'applique aussi bien pour les espaces vectoriels de dimension finie que pour les espaces hilbertiens ?
Merci d'avance !

par **Nightmare** » 27 Fév 2009, 01:29

Salut :happy3:

1) En général pour le calcul on partira de la relation fonctionnelle, on pourra par exemple prendre quelque valeurs particulières voir comment l'adjoint se comporte.

Petit rappel vu que tu le demande : T* est l'adjoint d'un opérateur T si pour tout x et tout y des espaces de Hilbert considérés, (Tx|y)=(x|T*y)

2)Bah il faut un produit scalaire quand même, dans ce cas oui, la définition est la même pour un endomorphisme.

par **barbu23** » 27 Fév 2009, 03:33

Bonsoir "Nightmare" : :happy2:
Par exemple : si on prend pour produit scalaire dans

( espaces des fonctions continues et continues par morceaux et :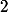

- periodique ! ( pour pouvoir choisir une jolie base qui a rapport avec les series de Fourier :happy2: ) )

c'est un produit scalaire !
On muni cet espace de la base suivante :

c'est même une base orthogonale ! :we: ( mais je ne sais pas si ça sert à quelques choses )Alors, d'après un théorème sur les series de Fourier ( je ne sais pas comment il s'appelle :hum: ) :
Toute fonction :

s'écrit :

( Parceque la serie de Fourier converge en tout point de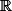

( il n'y'a pas de points de discontinuité ) :happy2: )
Maintenant, il reste à choisir un operateur simple pour lui chercher son adjoint par ce produit scalaire ! ( et c'est là que je ne sais pas comment m'y prendre :hum: )
Par exemple :
L'operateur

définie par :

et :

Voilà, donc, l'operateur

est définie à partir des images de la base de l'espace de depart !
Donc, comment trouver :

son adjoint ?
Merci de m'aider ! :happy2:
Cordialement !

par **barbu23** » 27 Fév 2009, 13:40

up ! :cry:

par **ShakkaChan** » 27 Fév 2009, 13:42

j'ai une question
t'es sur que tu munir peut C0 de ce produit scalaire et en faire un hilbert ??
j'ai jamais vu C0 etre un hilbert

par **Joker62** » 27 Fév 2009, 15:54

C_0 muni de la norme uniforme est complet
Muni de la norme 1 il n'en est plus un :o

Sinon le théorème des iso Banach dirait que les deux normes sont équivalentes or c'est faux :o

par **barbu23** » 27 Fév 2009, 18:40

Non pas besoin qu'il soit hilbertien ! mais juste prehilbertien ! non ? :we:

par **ShakkaChan** » 27 Fév 2009, 18:46

ben peut etre mais je crois pas que C0 est prehilbertien
je n'est jamais vu C0 muni d'un produit scalaire
tu l'as muni du produit scalaire L2 mais je suis pas sur du tout que tu puisse
t'as question est bien posé dans L2 , mais dans C0 ca me parait bizarre.
non ??

par **barbu23** » 27 Fév 2009, 19:00

ShakkaChan , regarde ici : :we:
http://c.caignaert.free.fr/chapitre12/node4.html

par **barbu23** » 27 Fév 2009, 19:09

ShakkaCahan :
Tu sais pourquoi,

n'est pas hilbertien ? Parceque,

n'est pas compact ... par contre :

est hilbertien !
Amicalement ! :we:

par **R.C.** » 27 Fév 2009, 19:35

Bonjour

barbu23 a écrit:ShakkaCahan :
Tu sais pourquoi, n'est pas hilbertien ? Parceque, n'est pas compact ... par contre : est hilbertien !
Amicalement ! :we:

J'aimerais bien savoir pour quel produit scalaire c'est hilbertien. Par pour celui que tu as donné : il est bien préhilbertien mais pas complet (le complété étant... L^2!!).
Pour revenir à ton exemple, tu peux calculer les coeff de la série de Fourier de T*f en fonction de ceux de f.

par **ShakkaChan** » 27 Fév 2009, 19:45

ok j'etais parti du principe que on faisait une integrale sur R j'avais pas vu qu'on etait sur (-pi,pi)
desolé

par **barbu23** » 27 Fév 2009, 19:58

Non, je crois que tu as rasion , on intègre sur

tout entier en le decoupant par morecaux de longueur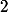

et on obtient à la fin la serie de Fourie que tu troves dans le lien que j't'ai montré ! et

n'est pas compact , donc l'espace des fonctions continues et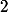

periodiques n'est pas hilbertien comme tu le dis !
Amicalement ! :we:

par **barbu23** » 27 Fév 2009, 20:06

R.C. a écrit:Bonjour

J'aimerais bien savoir pour quel produit scalaire c'est hilbertien. Par pour celui que tu as donné : il est bien préhilbertien mais pas complet (le complété étant... L^2!!).
Pour revenir à ton exemple, tu peux calculer les coeff de la série de Fourier de T*f en fonction de ceux de f.

Merci "RC" ! je vais essayer de le faire ! :happy2:

par **Olgierd** » 31 Mai 2015, 14:52

Chers Amis
La définition suivante de lopérateur adjoint est-elle valable uniquement pour un espace réflexif
(X** = X) ou bien elle est aussi valable pour un espace non-réflexif (X** ;) X)
=

Operateur adjoint !

Operateur adjoint !

Qui est en ligne