Convergence faible et opérateur compact

[melreg]

Bonjour,

A l'intérieur d'une preuve de mon cours d'analyse fonctionnelle, je trouve ceci:

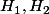
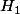
Soit , ( espaces de Hilbert) un opérateur compact. Soit une suite d'éléments de qui converge faiblement vers .

Puis, ce qui me plait moins:

Comme T est borné, alors converge faiblement vers dans .

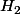
Je ne comprends pas l'implication...

J'espère ne rien avoir oublié pour que vous puissiez répondre à ma question... mais il ne me semble pas.

Merci d'avance!

[Nightmare]

Salut,

ton opérateur est borné :

Quelque soit n, .

Conclus !

[kazeriahm]

Hello,

c'est un resultat connu :

Si E et F sont des Banach, T : E -> F lineaire continu (fortement), alors T: E -> F est continu pour les topologies faibles de E et F.

http://fr.wikipedia.org/wiki/Topologie_faible#Continuit.C3.A9_des_op.C3.A9rateurs_et_topologie_faible

Il y a une demonstration dans le brezis, je peux scanner ca si tu veux

[melreg]

Salut,

ton opérateur est borné :

Quelque soit n, .

Conclus !

Ben j'ai de la peine à conclure justement. Je n'arrive rien à faire avec le terme ... . En fait voilà comment je suis parti:
Pour tout :

Mais après, pour pouvoir dire que est aussi petit que l'on veut j'aurais besoin de la convergence forte...

[kazeriahm]

.....ou comment etre ignore royalement.....

[melreg]

désolé kazeriahm... j'ai vu ton lien, mais il ne me satisfait pas vraiment, car j'aimerais bien alors démontré le résultat bien connu. Si tu veux me scanner la page, c'est volontiers, si ce n'est pas trop compliqué pour toi.

[mathelot]

bonsoir,

je me suis demandé (?):

on veut montrer que converge faiblement vers
dans .

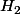
On teste cette condition sur les formes linéaires du dual
(topologique) de .



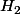
avec la transposée de T, le crochet de dualité s'écrit dans
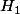
on applique l'hypothèse de la convergence faible dans
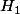
on transporte la limite par dualité dans (?)

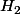
[melreg]

Salut mathelot,

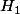
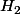
Par transposée de T, tu veux dire T*, l'opérateur adjoint? En fait, si et ne sont pas les mêmes, on ne peut pas parler de T*... non?

[mathelot]

Salut mathelot,

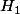
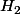
Par transposée de T, tu veux dire T*, l'opérateur adjoint? En fait, si et ne sont pas les mêmes, on ne peut pas parler de T*... non?

euh oui, ça doit être ça. L'adjoint.

si est une forme linéaire sur

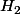
dépend linéairement de x et est donc une forme linéaire sur

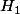
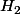
l'adjoint envoie le dual de sur le dual de

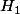
est-ce que tu peux remonter les propriétés de convergence faible
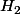
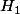
de vers via cette application ?

[melreg]

Merci mathelot.
Pour l'instant, je vois que je ne suis pas au niveau... il faut que je trouve une bonne référence sur le sujet...

[kazeriahm]

je suis desole, je n'ai pas pu scanner le truc

le bouquin est "Analyse fonctionelle", ecrit par Brezis, c'est sense etre une reference dans le domaine, disponible dans les BU je pense.

Bon courage

[melreg]

Merci quand même kazeriahm!

[amstramgram]

Salut melreg,

On peut quand même définir un opérateur adjoint si les espaces de Hilbert de départ et d'arrivée sont différents.

Si est un opérateur linéaire continu, alors il existe un unique opérateur linéaire continu tel que pour tout et pour tout , on ait



Je ne saurais pas trop répondre aux interrogations de mathelot mais je ne pense pas qu'il soit nécessaire de parler d'adjoint ici. Outre le résultat bien connu rappelé par kazeriahm, on peut peut-etre se servir du fait que la suite (x_n) étant faiblement convergente, elle est bornée et donc on peut extraire une suite x_{n_k} telle que T(x_{n_k}) converge dans H_2.

Mais c'est surement se compliquer la vie pour pas grand chose, à moins de vouloir démontrer le résultat plus intéressant qui dit que sous les mêmes hypothèses (T opérateur compact et suite x_n faiblement convergente vers x), alors fortement.