L3 Calcul différentiel

[JesterJ]

Bonjour à tous,

Après avoir fait des exos types de calculs différentiels (dérivées partielles, différentielles etc.), je tombe sur l'exercice suivant.

C'est simple, je n'ai strictement rien réussi à faire.

Une âme charitable pourrait tenter de le faire et partager sa correction (détaillée) svp ?

Je suis également preneur d'explications, même partielles.

Merci d'avance,
Jester

[checkmaths]

Euh quel exercice je n'en vois aucun...

[JesterJ]

Désolé, ça fait plusieurs fois que je tente de joindre l'image, mais elle ne s'affiche pas

[checkmaths]

https://www.maths-forum.com/guide-utilisation-f41/comment-inserer-une-image-t174537.html pour que la 1re méthode marche il faut que ton image fasse du 700×700.

[JesterJ]

Enfin ! Je te remercie ! Je pensais pas galérer autant rien que pour ça ahah !
Bref, je suis dispo si tu veux plus de précisions

[checkmaths]

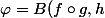Pour la 1re question, essaye de calculer la dérivée avec où est le produit scalaire qui est bilinéaire, et .

[JesterJ]

Justement, c'est la dérivée du produit scalaire qui me pose problème

[capitaine nuggets]

Salut !

1. Dériver un produit scalaire, c'est un peu comme dériver un produit de fonctions :



3. Utilise l'inégalité de la question précédente : supposons que f(x)=f(y), montre qu'alors x=y.

[checkmaths]

Exactement, mais on peut aussi le voir comme ça :

[JesterJ]

Bon...j'ai tenté mais vraiment ce produit scalaire me perturbe !

[checkmaths]

[JesterJ]

Oui, ça j'ai retrouvé, grâce à ce que tu as écrit juste au dessus

[checkmaths]

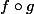
Tu n'as plus qu'à calculer la différentielle de , et .

[JesterJ]

Justement, h'(t), c'est bien (x-y)' ? Dans ce cas, on dérive par rapport à quoi ?

[checkmaths]

puisque est une constante par rapport à puisque ne dépend pas de .

[JesterJ]

Mais noooon !! Tout ça parce que j'avais pas relevé que c'était par rapport à t... désolé ahah !

Ca devrait donc fortement se simplifier !

[JesterJ]

Bon, encore une fois, je bafouille avec l'outil fourni.
Mais voici ce que je trouve:

B'(f\circ g, h)= B((f' \circ g).g',h) + B((f \circ g),0)

[checkmaths]

Oui c'est ça : .

[JesterJ]

Pas besoin d'aller plus loin dans le détail ? C'est suffisant de s'arrêter là ?

[checkmaths]

bah tu remplaces g et h et tu calcules g'(t) et c fini.