Calcul différentiel

[surf-555]

Bonsoir j'ai du mal avec ce chapitre donc voila ma question:
f(x,y)= 0 si x=0
y^2/x sinon
Je dois montrer que f n'est pas continue en 0 mais dérivable selon h en (0,0)....

merci d'avance

[fahr451]

bonsoir
f (0,0) = 0

g(x) = f(racine(x) , x) = 1 pour x>0

et si f était continue en 0 par composition des limites on aurait

x->0+ g -> f(0,0) = 1

[surf-555]

Ah Ok Merci

[BQss]

Bonsoir j'ai du mal avec ce chapitre donc voila ma question:
f(x,y)= 0 si x=0
y^2/x sinon
Je dois montrer que f n'est pas continue en 0 mais dérivable selon h en (0,0)....

merci d'avance

pour la dérivée selon h tu veux dire selon la droite y=x ou les droites y=ax peut-etre?

pour y=x par exemple:
lim h-->0 de f[(0,0)+(h,h)]-f(0;0)/ h=f(0+h,0+h)-f(0;0)/ h =h^2/h/h=1-->1 de dérivée 1 en 0 donc, c'est donc derivable en 0 suivant le chemin de vecteur(1,1).

[buzard]

pour la dérivée selon h tu veux dire selon la droite y=x ou les droites y=ax peut-etre?

à mon avis il parlait bien de la dérivé suivant la direction h=(h1,h2), un petit mots peu parfois eclaircire la situation.

mais bon, en France il est en effet courant d'utiliser la lettre h pour exprimer ce deplacement elementaire, dans les cours sur les dérivés et différentielles de fonctions dans les espaces de Banach.

[BQss]

à mon avis il parlait bien de la dérivé suivant la direction h=(h1,h2), un petit mots peu parfois eclaircire la situation.

mais bon, en France il est en effet courant d'utiliser la lettre h pour exprimer ce deplacement elementaire, dans les cours sur les dérivés et différentielles de fonctions dans les espaces de Banach.

bon ba si c'est ca(c'est effectivement bien maladroit d'utiliser la notation h pour le vecteur alors que c'est le scalaire multipliant le vecteur qu'on appelle h qui tend vers 0 et pas h1 et h2... mais bon) avec la notation que j'ai employé y=ax=h2/h1x (j'aurais plutot a ce moment la directement dit h2=ah1 avec h2 et h1 tendant vers 0 suivant la direction a), donc tel que h2=ah1 et donc h le vecteur (h1,ah1)) qui tend vers 0 quand h1 tend vers 0 suivant la direction a:

lim h1-->0 de f[(0,0)+(h1,ah1)]-f(0;0)/ h1=f(0+h1,0+ah1)-f(0;0)/ h1 =a^2h1^2/h1/h1=a^2-->a^2 de dérivée a^2 en 0 donc, c'est donc derivable en 0 suivant le chemin de vecteur h=(h1,h2)=(h1,ah1).

[buzard]

alors que c'est le scalaire multipliant le vecteur qu'on appelle h

et le produit scalaire de deux vecteurs ca sert a quoi alors?


je te rappele que la dérivé, suivant la direction h de f:E->F (ou E et F sont deux Banach) au point x de E, est la limite lorsque t->0 lorsqu'elle existe :

[BQss]

et le produit scalaire de deux vecteurs ca sert a quoi alors?


je te rappele que la dérivé, suivant la direction h de f:E->F (ou E et F sont deux Banach) au point x de E, est la limite lorsque t->0 lorsqu'elle existe :

On utilise pas suivant la direction "h" mais bon.

De plus, avec les notations de ta formule

On prend h un vecteur unitaire voyons et t est le scalaire . Il est strictement superflu de rajouter la valeur h au denominateur, c'est aussi ridicule que d'ecrire:
lim t-->0 f(xo+th)-f(xo)/th , ca n'a aucun interet.
Enfin on peut parler pour rien dire si tu aimes ca...

[BQss]

et le produit scalaire de deux vecteurs ca sert a quoi alors?


je te rappele que la dérivé, suivant la direction h de f:E->F (ou E et F sont deux Banach) au point x de E, est la limite lorsque t->0 lorsqu'elle existe :

oula oula quelle horreur, on confond tout la, (formule generale) , ta formule est fausse ce n'est pas la dérivée suivant un vecteur h ca, mais la dérivée suivant un vecteur unitaire u=h/||h||, donc soit le norme de h est de trop, soit il faut que tu changes le vecteur par rapport auquel tu derives par un vecteur u=h/||h|| en gardant telle quelle l'egalité de droite, de plus dans ma formule c'est h1 qui tends vers 0, c'est a dire que mon t c'est h1 et mon h c'est h1(1,a) voir ci dessous pour explication..

et tu dois confondre avec cette formule:

Ici on a ni besoin de gradient, ni besoin de produit scalaire. De plus ici f n'est meme pas continue donc pas differentiable et toi tu veux exprimer la dérivée selon le vecteur u a l'aide du gradient...

1)le produit scalaire n'a strictemnt rien a voir dans l'histoire. On parle juste de dérivée suivant un vecteur u, qui dans ma formule est la direction (1,a) si tu lis bien. Ou encore (1,h2/h1) ou encore suivant h=(h1;h2). Dans ma formule c'est h1 qui tend vers 0, c'est a dire une coordonnée de h, mais evidemment je fais tendre h2 en meme temps sur le chemin ah1, (il ne faut pas etre desorienté comme ca des qu'on bouscule un peu des notations, le h moi je le reserve a ce qui tend vers 0) ma formule a l'avantage de faire tendre h1 vers 0 : (h1;ah1)=h1(1,a) je n'ai pas besoin de t c'est h1 qui tends vers 0 et c'est la dérivée suivant le vecteur (1,a).

2) Il ne s'agit pas d'avoir un vecteur normé, c'est la dérivée suivant un vecteur et j'ai bien dit la dérivée suivant la direction h=(h1,h2)=h1(1,a) l'avantage dans ma formule c'est que c'est h1 qui tant vers 0 et h2 tant avec lui en fait pour garder la direction constante (avec h2=ah1)).

3) ici donc on a bien la dérivée en 0 selon le vecteur (1,a) de direction h (on peut l'appeler v) ( ici avec mon h=h1(1;a)=(h1;ah1)=(h1,h2)):
= = (attention h n'est pas constant dans cette formule, uniquement sa direction, il n'a rien a voir avec ton h qui est de norme fixé et ou c'est t qui tend vers 0, mon vecteur fixé implicite c'est (1,a). Et c'est par rapport a lui que je derive)

Si on veut retomber sur ta formule qui est la dérivée suivant un vecteur unitaire et pas la formule generale de la dérivée suivant un vecteur qulequonque: on peut faire:
implique
= = (attention au h qui n'est pas le meme h que dans ta formule)

je me cite au cas ou on me reprocherai de n'avoir pas precisé:

c'est donc derivable en 0 suivant le chemin de vecteur h=(h1,h2)=(h1,ah1).

Par ailleurs dériver suivant un vecteur normé n'a aucun interet pour savoir si f est derivable suivant la direction correspondante. Et il ne s'agit pas de produit scalaire, le norm(h) dans ta formule n'est pas la pour ca(voir ci dessus, tu nous a fait un mix avec la formule qui utilise le gradient, qui en l'occurence n'existe meme pas pour cette fonction) mais juste pour eventuellement normé le vecteur (mais on derive plus par rapport a h! mais par rapport a h/||h||...) et il faut alors changer le terme par rapport auquel au derive dans le membre de gauche.

Je te "rappelle" que si f est une application d'un ouvert U de E a valeur dans F
avec v un element de E et a appartient a U f admet une dérivée en a suivant le vecteur v si la limite suivante existe:

voir lien page 5
dérivée suivant le vecteur v et fonction gateau differentiable

un autre lien :
http://www.meca.unicaen.fr/Enseignement/Licence/Math/cours/node50.html
tout en bas de la page on voit ta formule corrigé pour la dérivée selon un vecteur unitaire y=h/||h||(selon tes notations, si on remplace h par y dans le membre de gauche dans ta formule elle devient juste) .

[fahr451]

je n'ai pas lu la polémique mais un petit rappel :

dérivable suivant tout vecteur h non nul ( la notation est usuelle) équivaut à existence des dérivées partielles


pour df/dx (0,0)

on écrit l 'application partielle :

g(x) = f(x,0) qui est identiquement nulle donc sa dérivée en 0 est nulle donc
df/dx (0,0) = 0


pour df/dy (0,0)

on écrit l application partielle

g(y) = f(0,y) identiquement nulle également donc

df/dy(0,0) = 0

la dérivée suivant un vecteur h = (h1,h2) est alors

0

[BQss]

Salut Fahr,

avec v=(1,a) par exemple
= = =

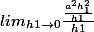Ou n'es tu pas d'accord?

dérivable suivant tout vecteur h non nul ( la notation est usuelle) équivaut à existence des dérivées partielles

Soit, mais pourquoi ces dérivées partielles seraient alors egales aux dérivées suivant tout vecteur h?

Je rappelle que meme si les dérivées partielle existe en 0 elle ne sont pas continue en 0, car la fonction n'est meme pas continue en 0.
La fonction n'est pas differentiable en 0.

et cette formule:



n'est pas valable ici.

Tu utilises alors cette formule explicite?

valable si les dérivées partielles existes(ne faut-il pas qu'elles soient en plus continues...).

Mais alors si non comment expliques tu que je trouve des dérivées de a^2 suivant les vecteur (1,a), ou serait l'erreur dans le calcul explicite au debut du post? Je ne suis pas d'accord avec ton resultat. Juste sur le fait que les dérivées suivant tout vecteurs existent, mais je ne suis pas d'accord sur la valeure 0...

[BQss]

Fahr je ne suis pas d'accord avec ton resultat comme quoi la dérivée suivant tout vecteur serait nul, regarde ici un autre exemple:
sur ce lien la dérivée suivant tout vecteur n'est pas nulle, pourtant les dérivéee partielle en (0;0) valent 0. Sur ce lien la fonction n'est pas non plus continu en 0 et donc pas differentiable...

http://www.cyber.uhp-nancy.fr/demos/MATH-DIF/2fonctions/node14.html

On peut prendre un vecteur h=(u,v) a la place de (1,a) si tu veux,

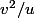Ici cela donne = qui est different de 0 si u et v sont differents de 0... Et ca vaut 0 seuleument si u ou v vallent 0.

[fahr451]

absolument j 'ai déraillé

f n 'est pas différentiable


les dérivées partielles sont nulles

pas la dérivée suivant h

on doit revenir à la définition

g'(0) avec g(t) = f (0+th)