Séries numériques

par **VictorT** » 27 Déc 2015, 17:16

Bonjour, jai un soucis sur un exercice.

Soit Un= ln (1 + ( (-1) ^n / n ) )

1°) Trouver le plus petit entier n0 tel que un0 est définie. ( Je pense que n0 = 2, est-ce le cas ? )

2°) Démontrer que la série somme des Un converge

3°) Calculer la somme.

Je ne sais pas du tout comment démontrer ( sans calculer la somme ) que la série est convergente.

Pour le calcul de la somme je l'ai décomposée de la façon suivante:
Somme de 2 à n = ln(3/2)+ln(2/3)+ln(5/4)+ln(4/5)+...

= ln( 3x2x5x4x7x6x9x8x...x(n+1)xn / 2x3x4x5x..xn )

= ln ( (n+1)! / n! ) = ln ( n+1 )

je trouve donc que la série diverge, ce qui est contraire a 2°).

Merci de me lire

par **Robot** » 27 Déc 2015, 17:21

Critère de convergence pour les séries alternées ?

Et revois ton calcul pour la somme.

par **VictorT** » 27 Déc 2015, 17:30

Robot a écrit:Critère de convergence pour les séries alternées ?

Et revois ton calcul pour la somme.

Merci pour ton retour je vois pour la convergence.

Pour ce qui est du calcul, je n'arrive pas à généraliser le numérateur (3x2x5x4...) ...

par **MouLou** » 27 Déc 2015, 17:33

Revois ton calcul oui. Sinon tu peux calculer les limites S2n et S2n+1

par **VictorT** » 27 Déc 2015, 17:39

Ok merci je vais essayer.

par **chan79** » 27 Déc 2015, 17:46

Salut
Calcule d'abord S(4),S(6),S(8).. avec S(n)=somme des U(i) pour i variant de 2 à n

par **VictorT** » 27 Déc 2015, 17:58

MouLou a écrit:Revois ton calcul oui. Sinon tu peux calculer les limites S2n et S2n+1

S2n = ln(5/4)+ ln(7/6)+ ln(9/8) + ... + ln(n^2+1/n^2)

S2n+1 = ln (4/5) + ln (6/7)+... + ln ( n^2/n^2+1)

lim S2n = lim S2n+1 =0

Donc lim Sn = 0

3°) Somme = 0 ?

Est-ce bien cela?

par **MouLou** » 27 Déc 2015, 18:03

Pour le résultat oui, pour le calcul non. S2n c'est la somme des premiers termes de 2 à 2n, pas la somme des termes pairs.

par **VictorT** » 27 Déc 2015, 18:07

MouLou a écrit:Pour le résultat oui, pour le calcul non. S2n c'est la somme des premiers termes de 2 à 2n, pas la somme des termes pairs.

Ok merci beaucoup

par **mathelot** » 27 Déc 2015, 18:58

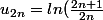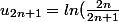donc

La sommation de la série peut être associative (addition par paquets de longueur fixée)
mais pas commutative.

par **VictorT** » 27 Déc 2015, 22:20

mathelot a écrit: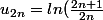

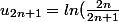donc

La sommation de la série peut être associative (addition par paquets de longueur fixée)
mais pas commutative.

Merci de votre réponse.

Pour le détail est-bien ça:

S2n+1=ln(3/2)+ln(2/3)+ln(5/4)+ln(4/5)+...+ ln(2n/2n+1) = ln (3) - ln(2) + ln(2) - ln(3) +... =
ln(2n/2n+1 )

lim (2n / 2n+1 ) = ln (1 ) = 0 ???

Séries numériques

Séries numériques

Qui est en ligne