Primitives/logarithme népérien

[laetidom]

ha ! La plus simple me va...

ah, je calcules et te dis . . . (je prends en cours donc moins facile . . .)

[Norma]

Non mais tu semblais rejoindre ce que annick disait non? C'est ça qui me semble le plus simple, enfin ça m'est égal tant que je comprends.. ta méthode peut très bien m'aller!!

[laetidom]

Non mais tu semblais rejoindre ce que annick disait non? C'est ça qui me semble le plus simple, enfin ça m'est égal tant que je comprends.. ta méthode peut très bien m'aller!!

Oui c'est celle que j'ai fait mais les deux sont équivalentes :

[laetidom]

Je viens de vérifier avec l'approche de mathelot et le résultat est identique ! On s'en doutait mais ça rassure !

Le plus important est de savoir si toi, tu comprends ?

[Norma]

Bonsoir,

J'essaye d'apporter ma petite pierre :



et l'IPP devant ressembler à :

alors on a :

choix important :

====> calcul de

====> calcul de

Je reprends tes déductions d'avant et je ne comprends pas :

si

alors pourquoi on écrit pas que u'=

et que v= 1 ?

ou que u'=1

et v =

[laetidom]

Oui, on aurait pu prendre l'autre option, ça marche pareil, arbitrairement on a pris u=ln... et v'=1

en fait, si l'on choisi cette version c'est que c'est plus facile . . .


Je viens de vérifier avec le programme de la calculatrice le résultat que je t'ai donné et ça confirme !

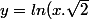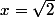
En fait, l'aire comprise entre , l'axe des abscisses et les 2 verticales (en x=1 et vaut 0,2194709908 ua

[Norma]

Ducoup laquelle des "propositions" que j'ai faite est juste ?

[laetidom]

Ducoup laquelle des "propositions" que j'ai faite est juste ?

soit on choisi : u = ln... et v' = 1
soit : u=1 et v'=ln...

moi j'ai fait avec la première !

[Norma]

Oui, on aurait pu prendre l'autre option, ça marche pareil, arbitrairement on a pris u=ln... et v'=1

en fait, si l'on choisi cette version c'est que c'est plus facile . . .


Je viens de vérifier avec le programme de la calculatrice le résultat que je t'ai donné et ça confirme !

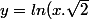En fait, l'aire comprise entre , l'axe des abscisses et les 2 verticales (en x=1 et vaut 0,2194709908 ua

Atteeeeend c'est la question d'après j'y suis pas encore

[laetidom]

Atteeeeend c'est la question d'après j'y suis pas encore

ok, ok !

[Norma]

Ducoup laquelle des "propositions" que j'ai faite est juste ?

soit on choisi : u = ln... et v' = 1
soit : u=1 et v'=ln...

moi j'ai fait avec la première !

Je ne comprends toujours pas:

Dans on a pas v' ... ni u donc il faut déduire v' et u de v et u' , donc c'est bien u et v' qu'il faut remplacer par ln.. ou 1 non?

[laetidom]

DEF IPP : int (u'.v) = [uv] - int (u.v')

donc tu vois que l'on a besoin de tout,

au debut il faut faire un choix et dans la seconde intégrale on fait le produit de uv' si c'est u'v qui a était choisi en premier

ca va venir, ne t'inquiètes pas ! (j'ai inséré un schéma plus haut)

[Norma]

Mais je ne dis pas le contraire... j'arrive pas à me faire comprendre... tu dis que par exemple u = ln... et v'= 1 mais on a

donc si on remplace on peut que dire alors que u'=1 ou u'=ln... et que v=1 ou v=ln , si u'=1 u sera la primitive de 1 et si u'=ln u sera la primitive de ln... mais donc on peut pas dire que u=ln... tu vois ce que je veux dire et ce que je ne comprends pas ?

[laetidom]

ah oui je vois ton bloquage ! :

. . . fin de journée . . . je te dis

[mathelot]

@Norma: si tu poses v'=ln(x), il faut trouver une primitive v de v', qui est xln(x)-x
mais cette primitive est obtenue par intégration par parties en posant v'=1
donc on tourne en rond et la seule issue est de poser v'=1 et u=ln()

[Norma]

ah oui je vois ton bloquage ! :

. . . fin de journée . . . je te dis

Pauvre de toi !

@Norma: si tu poses v'=ln(x), il faut trouver une primitive v de v', qui est xln(x)-x
mais cette primitive est obtenue par intégration par parties en posant v'=1
donc on tourne en rond et la seule issue est de poser v'=1 et u=ln()

je m'enfonce ... c'est énervant

[laetidom]

oui nous ça ne nous a pas gêné avec l'habitude mais comme la DEF est :

" int (u'v) = [ uv] - int(uv')

u'=1 et v=ln... pour l'int 1

donc on calcule u=x et v'=1/x pour la seconde


Je pense que Norma sera moins perturbée comme ça, mais ça ne change rien au résultat déjà énoncé !

Pauvre de toi !

: ça va aller ! (sourire)

[laetidom]

Tu es ok sur les calculs . . . ?

[Norma]

oui nous ça ne nous a pas gêné avec l'habitude mais comme la DEF est :

" int (u'v) = [ uv] - int(uv')

u'=1 et v=ln... pour l'int 1

donc on calcule u=x et v'=1/x pour la seconde


Je pense que Norma sera moins perturbée comme ça, mais ça ne change rien au résultat déjà énoncé !

Pauvre de toi !

: ça va aller ! (sourire)

Alors si (u'v)=[u-v]-(uv')

donc

??? Si c'est pas ça je reviens demain parceque je crois que je vais chialer

[laetidom]

Alors si (u'v)=[uv]-(uv') ===> attention, à l'intérieur ce sont des produits

donc =

??? Si c'est pas ça je reviens demain parceque je crois que je vais chialer

ok

donc ça donne primitive de xln... (de 1 à rac2) - intégrale de 1 (de 1 à rac2)

donc ça donne primitive de xln... (de 1 à rac2) - primitive de x (de 1 à rac2)


Comprends-tu ?