Primitives/logarithme népérien

[Norma]

Alors si (u'v)=[uv]-(uv') ===> attention, à l'intérieur ce sont des produits

donc =[x.ln(x\sqrt{2})]- int (x.\frac{1}{x})[/tex]

??? Si c'est pas ça je reviens demain parceque je crois que je vais chialer

ok

ok je reviens demain ?

[laetidom]

CA MARCHE !

A demain ! Bonne soirée !

[Ben314]

Salut,
Je vais essayer "d'en remettre une couche" pour voir si ça clarifie :
D'un coté, tu as l'intégrale que tu veut calculer et d'un autre coté, tu as la formule d'intégration par parties qui te dit que (qui est en fait une façon à peine différente d'écrire que (uv)'=u'v+uv').
Et tu te pose la question de savoir "qui est qui" là dedans et... la réponse est extrêmement simple :
La formule d'intégration par partie, elle est, heureusement, valable pour n'importe quelle fonctions (régulières) u et v donc tu peut prendre absolument n'importe quoi pourvu que le produit u'(x)v(x) soit bien égal à la fonction que tu cherche à intégrer.
Par exemple, tu pourrait parfaitement prendre :
(a) u'(x)=1 ; v(x)=
(b) u'(x)= ; v(x)=1
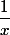
(c) u'(x)= ; v(x)=
(d) u'(x)=x ; v(x)=
(d) u'(x)= ; v(x)=
etc, etc, etc...
Ensuite, la VRAIE question, c'est de comprendre pourquoi on fait un certain choix plutôt qu'un autre (ici, par exemple, seul le choix (a) est judicieux) et de nouveau la réponse est on ne peut plus simple : dans l'intégration par partie, déjà, pour pouvoir mener les calculs, il faut connaitre une primitive du terme qu'on a choisi de prendre pour u'(x) donc par exemple, ça élimine les choix du style du (b) ou du (e) où on ne connait pas de primitive de u.
Ensuite, il faut bien voir qu'à droite du = (dans une intégration par parties), il y a de nouveau une intégrale et qu'évidement, si cette nouvelle intégrale est plus compliquée que celle de départ, ce qu'on aura écrit sera parfaitement juste, mais ça servira à que dalle. Donc pour que ça serve à quelque chose, il faut non seulement que l'on puisse trouver une primitive u de u', mais aussi que le produit uv' soit "plus simple" que le produit de départ u'v. Et là, si tu regarde tout le choix proposés ci dessus, tu constatera que le seul et unique cas où le uv' d'arrivé est (nettement) plus simple que le u'v de départ, c'est le choix (a).
Et si on veut revenir au problème de départ, ça s'explique par le fait que la fonction ln est une fonction "compliquée", mais dont la dérivée est simple, donc il faut absolument poser v(x)=ln(???) pour que le v' soit plus simple que v (tu vérifiera que, si on prenait par exemple v(x)=x.ln(???), le ln ne disparaitrait pas complètement dans le v'(x).
Et pour continuer dans la liste des "on a le choix", il faut aussi se rendre compte (il y a des exercices où ça sert) que lorsque l'on dit par exemple que l'on prend u'(x)=1, il y a plusieurs choix pour u(x). Le premier qui vient à l'esprit est évidement u(x)=x, mais on pourrait parfaitement prendre u(x)=x-5 ou bien u(x)=x+17 si ça facilitait les calculs (ce qui n'est pas le cas ici) : essaye si tu veut avec u(x)=x+1 pour vérifier que ça donne bien le même résultat (après un peu plus de calculs).

En résumé, l'intégration par parties, ça fait partie des outils extrêmement simple du calcul intégral dans le sens qu'il faut même pas une ligne pour justifier que cette égalité est valable. Sauf que d'un autre coté, c'est un outil compliqué, dans le sens qu'il y a des tas de contextes relativement différents où c'est extrêmement utile donc qu'on met un bon moment à comprendre toute la "puissance" de l'outil en question (i.e. à voir l'ensemble des exercices où c'est utile de faire des i.p.p.).

[Norma]

CA MARCHE !

A demain ! Bonne soirée !

Quand j'ai dis je reviens demain ? C'était pour demander si ton ok voulait dire que ce j'ai fais était ok ou si tu me faisais comprendre que je pouvais revenir demain vu que je me suis plantée ?

Bon alors effectivement ça m’éclaire un peu plus cette explication merci ! Je pense que je vais me l'imprimer et l'encadrer !!!

Maintenant quand du coup on écrit

A quoi ça me sert à la base alors d'écrire ? A remplacer pour résoudre/réduire?

Laetidom je n'arrive pas bien à déchiffrer ducoup la résolution que tu as proposé sur ta feuille quadrillée

[laetidom]

Bonjour Norma,

CA MARCHE !

A demain ! Bonne soirée !

Quand j'ai dis je reviens demain ? C'était pour demander si ton ok voulait dire que ce j'ai fais était ok oui !ou si tu me faisais comprendre que je pouvais revenir demain vu que je me suis plantée ?

Bon alors effectivement ça m’éclaire un peu plus cette explication merci ! Je pense que je vais me l'imprimer et l'encadrer !!! tu vois ça va venir ! Pas de soucis !

A quoi ça me sert à la base alors d'écrire ? ====> c'est la méthode de mathelot A remplacer pour résoudre/réduire?

Laetidom je n'arrive pas bien à déchiffrer du coup la résolution que tu as proposé sur ta feuille quadrillée ===> Je complète :

[Norma]

Bonjour !

ok j'ai compris, je vais me faire des grosses fiches avec toutes les propriétés/formules. Merci... 1000 fois! J'ai trouvé des exercices pour m'entraîner aussi.

Pour l'aire, le cours me dis que l'aire d'un rectangle est environ égale à la somme f(x) dx

et que l'aire totale est environ égale à la somme des f(x)dx de x égal à a à x égal à b.

D'après ce que Laetidom semblait dire c'est que dans ce cas là l'aire est égale à ce qu'on vient de calculer. Mais je ne comprends pas la deuxième partie vous auriez un exemple , c'est exactement ce qu'on vient de faire non?

J'ai l'allure des courbes, dans le schémas, C est positive, mais C' est négative

ici on parle de ce qu'on a calculé avec a=1 et b=

L'énoncé dit : Soit D l'ensemble des points M dont les coordonnées vérifient :

et

Calculer l'aire du domaine en cm^2. On donnera la valeur exacte puis une valeur approchée à 10^{-2}

Je dois calculer les deux aires et les additionner?

[laetidom]

Salut Norma,

Content de voir que ça progresse !

[Norma]

Donc je calcule



et ?

[laetidom]

Donc je calcule

oui !
et ? oui !

En regardant mon graphe ci-avant, le résultat de la première intégrale sera >0 (au-dessus de l'axe des abscisses), la seconde <0 (au-dessous), donc pour le résultat final attendu : résultat de C + la valeur absolue du résultat de C'.

Info pour contrôler ton résultat littéral final : je trouve une aire (entre les bornes et entre C et C') de 0,814383855 . . . (tout en sachant que cette valeur numérique ne sert qu'à contrôler la justesse d'un résultat, elle n'est à inscrire sur une copie que si c'est demandé ! dans le cas contraire, c'est le résultat littéral qui est attendu !)

[Norma]

J'ai du m'absenter, je vais plancher dessus ce soir et demain. Merci!

[laetidom]

J'ai du m'absenter, je vais plancher dessus ce soir et demain. Merci!

Aucun problème ! Bon courage et bonne soirée.

[Norma]

pour

Est-ce que je peux utiliser la formule ?

Si oui j'ai

Où je ne sais pas quoi faire de mon , si je cherche je ne vois pas comment le trouver, avec ln?

[laetidom]

pour

Est-ce que je peux utiliser la formule ? oui !

Si oui j'ai

Où je ne sais pas quoi faire de mon , si je cherche je ne vois pas comment le trouver, avec ln?

très bien !

la primitive de est

[Norma]

pour

Est-ce que je peux utiliser la formule ? oui !

Si oui j'ai

Où je ne sais pas quoi faire de mon , si je cherche je ne vois pas comment le trouver, avec ln?

très bien !

la primitive de est

-1 ou 1 ? on garde le signe ?

[laetidom]

rq : à la fin de l'intégrale toujours marquer "dx",

[(x²/2) - e^-x] me convient !

et donc [(x²/2) - e^-x] = ( . . . - . . . ) - ( . . . - . . .) = ?

[Norma]

si c'est mx et m au dénominateur c'est pas 1 alors ? ha si -1 pardon j'avais compris ta réponse tout de suite

[laetidom]

si c'est mx et m au dénominateur c'est pas 1 alors ?

dans ce cas de figure oui m = -1 qui correspond au signe - entre le premier et le second terme à l'intérieur des crochets.

[Norma]

Oui j'ai percuté en envoyant mon message.

[laetidom]

Oui j'ai percuté en envoyant mon message.

les crochets que sur la première ligne,
des parenthèses sur la seconde,

[Norma]

d'accord, le calcul est juste?