Equation de droite
97 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Equation de droite
Bonjour.
Je cherche de l'aide pour cet exercice dont je ne comprends pas très bien le sens.
On considère dans un repère orthonormé la droite d'équation (1-m²)x+2my+m²-2m-3=0. Par un point donné passent en général deux droites.
1) Trouver le lieu des points par où passent deux droites D confondues.
2)Trouver le lieu des points par où passent deux droites D perpendiculaires.
Merci.
Je cherche de l'aide pour cet exercice dont je ne comprends pas très bien le sens.
On considère dans un repère orthonormé la droite d'équation (1-m²)x+2my+m²-2m-3=0. Par un point donné passent en général deux droites.
1) Trouver le lieu des points par où passent deux droites D confondues.
2)Trouver le lieu des points par où passent deux droites D perpendiculaires.
Merci.
Re: Equation de droite
Bonjour
D'abord l'énoncé est très mauvais. Où as tu pris cet exercice.
Ce qui fait que je ne comprends pas la première question (mais pas du tout) .
Pour la deuxième question, je la devine mais encore une fois c'est pas le but du jeu. Il faut d'abord un énoncé clair.
Voilà comment j'interprète l'exercice : D'abord il n'y a pas une droite mais pour tout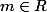
on associe une droite d'équation ..... (qu'il vaut mieux appeler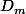 )
)
La deuxième question serait (d'après moi) déterminer le lieu des points du plan qui sont l'intersection de 2 droites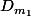 et
et 
Je pense qu'avant d'aller plus loin il faut que l'on soit d'accord pour un énoncé correct.
D'abord l'énoncé est très mauvais. Où as tu pris cet exercice.
Ce qui fait que je ne comprends pas la première question (mais pas du tout) .
Pour la deuxième question, je la devine mais encore une fois c'est pas le but du jeu. Il faut d'abord un énoncé clair.
Voilà comment j'interprète l'exercice : D'abord il n'y a pas une droite mais pour tout
on associe une droite d'équation ..... (qu'il vaut mieux appeler
La deuxième question serait (d'après moi) déterminer le lieu des points du plan qui sont l'intersection de 2 droites
Je pense qu'avant d'aller plus loin il faut que l'on soit d'accord pour un énoncé correct.
Re: Equation de droite
Bonjour,
Il s'agit de droites paramétrées par un paramètre m.
Par un point donné M(x,y), passent en général 2 droites, distinctes ou confondues, ou aucune : il s'agit de résoudre l'équation de la droite d'inconnue m, avec x et y étant des constantes données.
C'est une équation du 2nd degré en m : il y a en général 2 solutions m1 et m2, distinctes ou confondues, ou aucune..
Les droites sont confondues à quelle condition sur m1 et m2 ?
Pas vu ton message @aviateur : si, l'énoncé est correct.
Il s'agit de droites paramétrées par un paramètre m.
Par un point donné M(x,y), passent en général 2 droites, distinctes ou confondues, ou aucune : il s'agit de résoudre l'équation de la droite d'inconnue m, avec x et y étant des constantes données.
C'est une équation du 2nd degré en m : il y a en général 2 solutions m1 et m2, distinctes ou confondues, ou aucune..
Les droites sont confondues à quelle condition sur m1 et m2 ?
Pas vu ton message @aviateur : si, l'énoncé est correct.
Modifié en dernier par Pseuda le 19 Aoû 2018, 22:45, modifié 1 fois.
Re: Equation de droite
Rebonjour @pseuda
alors la première question serait si elle est bien posée ??
1. Déterminer le lieu des points A tels qu'il passe une droite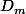 et une seule par ce point A.
et une seule par ce point A.
Mais néanmoins je veux un énoncé correct. En effet c'est très mal dit mais en y regardant de plus près cela
me semble faux.
"En général par un point passe 2 droites" (de la famille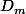 ). Et bien ça c'est faut.
). Et bien ça c'est faut.
Il y a une infinité de points où ne passe aucune droite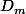
alors la première question serait si elle est bien posée ??
1. Déterminer le lieu des points A tels qu'il passe une droite
Mais néanmoins je veux un énoncé correct. En effet c'est très mal dit mais en y regardant de plus près cela
me semble faux.
"En général par un point passe 2 droites" (de la famille
Il y a une infinité de points où ne passe aucune droite
Re: Equation de droite
Remarque:
si on prend les choses comme cela alors en répondant à cette première question on voit que l'énoncé est douteux.
En effet fixons M=(x,y) appartenant au plan. Quelles sont les droites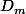 qui passent par M?
qui passent par M?
Ceux sont les droite associées à m tel que
x+2*m y+m^2-2*m-3=0)
Soit encore telles que
*m^2+ 2(y-1) m+x-3=0.)
C'est un polynôme du second degré (si x=1) de la variable m dont le discriminant réduit est
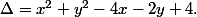 (1)
(1)
Or l'équation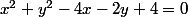 et l'équation du cercle C(I,r) de centre le point I=(2,1) et de rayon r=1.
et l'équation du cercle C(I,r) de centre le point I=(2,1) et de rayon r=1.
Tout point M situé à l'intérieur de C vérifie donc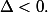
C'est à dire que l'on a bien ici une infinité de points où aucune droite de la famille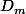 ne passent.
ne passent.
!!!!!!!!! !!!!!!!!
Maintenant si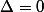 l'équation (1) admet une racine double, c'est à dire qu'il ne passe qu'une droite et une seule D_m par ce point .
l'équation (1) admet une racine double, c'est à dire qu'il ne passe qu'une droite et une seule D_m par ce point .
En conclusion (modulo la remarque ci-dessous) la réponse à la question 1 est: le lieu recherché est le cercle C.
Attention je n'ai pas regardé le cas x=1 c'est à étudier.
si on prend les choses comme cela alors en répondant à cette première question on voit que l'énoncé est douteux.
En effet fixons M=(x,y) appartenant au plan. Quelles sont les droites
Ceux sont les droite associées à m tel que
Soit encore telles que
C'est un polynôme du second degré (si x=1) de la variable m dont le discriminant réduit est
Or l'équation
Tout point M situé à l'intérieur de C vérifie donc
C'est à dire que l'on a bien ici une infinité de points où aucune droite de la famille
!!!!!!!!! !!!!!!!!
Maintenant si
En conclusion (modulo la remarque ci-dessous) la réponse à la question 1 est: le lieu recherché est le cercle C.
Attention je n'ai pas regardé le cas x=1 c'est à étudier.
Re: Equation de droite
Pour la deuxième question voici quelques indications mais attention à bien faire les choses.
En effet dans ce genre d'exercice il faut de la rigueur sinon le danger c'est d'oublier les cas particuliers.
Conseil 1. Bien finir la question 1.
question 2. Il faut d'abord considérer un point M=(x,y) qui dans l'ensemble solution précédent.
Vu la question 1. on suppose d'abord que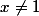 et
et 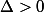
Donc l'équation
(1-x)*m^2+2(y-1)m +x-3=0
admet 2 solutions notées
Les droites correspondantes sont perpendiculaires ssi les vecteurs normaux sont orthogonaux,
i.e.(1-m_2^2,2 m_2)=0)
où encore
=0) où j'ai posé
où j'ai posé  et
et 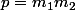
Mais s=-2(y-1)/(1-x) et p=(x-3)/(1-x).
Ce qui donne une équation vérifiée par x et y. En simplifiant cela donne une conique 'je crois même que c'est un cercle)
Voilà grosso modo voici comment faire. Encore une fois, je le répète il y a une finition à faire proprement.
En effet dans ce genre d'exercice il faut de la rigueur sinon le danger c'est d'oublier les cas particuliers.
Conseil 1. Bien finir la question 1.
question 2. Il faut d'abord considérer un point M=(x,y) qui dans l'ensemble solution précédent.
Vu la question 1. on suppose d'abord que
Donc l'équation
(1-x)*m^2+2(y-1)m +x-3=0
admet 2 solutions notées
Les droites correspondantes sont perpendiculaires ssi les vecteurs normaux sont orthogonaux,
i.e
où encore
Mais s=-2(y-1)/(1-x) et p=(x-3)/(1-x).
Ce qui donne une équation vérifiée par x et y. En simplifiant cela donne une conique 'je crois même que c'est un cercle)
Voilà grosso modo voici comment faire. Encore une fois, je le répète il y a une finition à faire proprement.
Re: Equation de droite
Merci pour vos réponses. Je vais les étudier. J'ai du m'absenter.
Il s'agit de l'exercice 734 de Géométrie 1ere C de Lebossé Hémery version 1966.
Il s'agit de l'exercice 734 de Géométrie 1ere C de Lebossé Hémery version 1966.
Re: Equation de droite
oui mais moi je n'ai aucun livre de lycée. Si tu peux scanner l'énoncé je suis un peu curieux de voir comment il est formulé. Cela m'étonnerait tout de même qu'il soit formulé comme tu le dis.
Néanmoins c'est un très bon exercice de lycée
Tu peux essayer de le voir en détail, si tu as des questions on pourra t'aider./
Néanmoins c'est un très bon exercice de lycée
Tu peux essayer de le voir en détail, si tu as des questions on pourra t'aider./
Re: Equation de droite
@aviateur C'est un exercice très classique du lycée, son libellé est correct. Je me souviens l'avoir eu (ou ce genre) dans mes classes. C'est vrai que ce genre d'exercice de courbes à paramètres est moins couramment donné aujourd'hui, mais certains profs en donnent.
J'en ai discuté une fois avec un professeur d'Université qui se plaignait que les élèves sortis du lycée ne savaient plus résoudre des équations à paramètres.
J'en ai discuté une fois avec un professeur d'Université qui se plaignait que les élèves sortis du lycée ne savaient plus résoudre des équations à paramètres.
Re: Equation de droite
@pseuda Je ne sais pas si tu as vraiment compris mon problème.
Ce que je ne comprends pas c'est que l'énoncé est très très mal dit. A un tel point que sur le coup je n'ai pas compris la première question et j'ai dû deviner la deuxième.
Et j'ai un fort doute sur le fait que l'exercice soit formulé tel quel dans un livre.
Je peux concevoir que l'auteur du livre n'a pas vu qu'il y a une infinité de points situés sur aucune des droites de la famille.
Mais que l'énoncé ne soit pas clair du tout c'est autre chose. A ma connaissance je n'ai jamais vu un énoncé aussi douteux dans un livre.
Déjà posso49 cherche de l'aide pour un exercice dont il ne comprend pas bien le sens.
Et bien s'il est posé comme cela (l'exercice) qu'il ne s'inquiète pas c'est normal.
Mais malgré tout......??
Ce que je ne comprends pas c'est que l'énoncé est très très mal dit. A un tel point que sur le coup je n'ai pas compris la première question et j'ai dû deviner la deuxième.
Et j'ai un fort doute sur le fait que l'exercice soit formulé tel quel dans un livre.
Je peux concevoir que l'auteur du livre n'a pas vu qu'il y a une infinité de points situés sur aucune des droites de la famille.
Mais que l'énoncé ne soit pas clair du tout c'est autre chose. A ma connaissance je n'ai jamais vu un énoncé aussi douteux dans un livre.
posso49 a écrit:Bonjour.
Je cherche de l'aide pour cet exercice dont je ne comprends pas très bien le sens.
On considère dans un repère orthonormé la droite D d'équation (1-m²)x+2my+m²-2m-3=0. Par un point donné passent en général deux droites.
1) Trouver le lieu des points par où passent deux droites D confondues.
2)Trouver le lieu des points par où passent deux droites D perpendiculaires.
Merci.
Déjà posso49 cherche de l'aide pour un exercice dont il ne comprend pas bien le sens.
Et bien s'il est posé comme cela (l'exercice) qu'il ne s'inquiète pas c'est normal.
Mais malgré tout......??
Re: Equation de droite
Merci Pseuda pour ta réponse. Quant à Aviateur, je suis désolé pour ton manque de confiance que je n'apprécie pas du tout.
Re: Equation de droite
Je t'aide et puis tu as le culot de me critiquer et cela ressemble plus à une insulte qu'à une critique. Alors scan moi l'exercice!!
C'est inadmissible que des gamins qui demandent de l'aide se permettent de mettre en doute les interrogations légitimes des personnes qui donne leur temps à aider les jeunes bénévolement.
Par ailleurs au lieu de ne pas apprécier mon étonnement concernant l'énoncé, tu aurais mieux fait d'apprécier l'aide que je t'ai apporté.
C'est inadmissible que des gamins qui demandent de l'aide se permettent de mettre en doute les interrogations légitimes des personnes qui donne leur temps à aider les jeunes bénévolement.
Par ailleurs au lieu de ne pas apprécier mon étonnement concernant l'énoncé, tu aurais mieux fait d'apprécier l'aide que je t'ai apporté.
Re: Equation de droite
Cher aviateur, j'ai 67 ans et je fais des maths pour mon plaisir. Dans ce manque de confiance, je n'apprécie pas du tout l'aide que tu donnes, et je n'ai pas d'ordre à recevoir d'un gamin comme toi.
La réponse de Pseuda était plus adaptée. Apprend à savoir à qui tu parles sur un forum.
La réponse de Pseuda était plus adaptée. Apprend à savoir à qui tu parles sur un forum.
Re: Equation de droite
Pseuda avait très bien compris le problème, et avec l'explication de son premier message, je l'ai compris également et suis d'accord avec lui pour dire que le libellé de cet exercice est correct, même s'il est un peu déroutant. Aussi, seule cette première réponse de Pseuda m'interessait et n'ai donc pas étudié les tiennes.
Par ailleurs, je donne moi aussi de mon temps pour aider des élèves.
Par ailleurs, je donne moi aussi de mon temps pour aider des élèves.
Re: Equation de droite
Salut,
Ensuite, concernant l'énoncé, non, il n'est absolument pas "correct" :
- Déjà la phrase "Par un point donné passent en général deux droites" devrait évidement être précédée de "On admet que" ou bien "Démontrer que".
- Ensuite, dans cette même phrase, je suis certain (*) que pour plus de la moitié des élèves de terminale le sens du "en général" va être mal compris.
Jusque là, c'est pas super gênant et c'est pas plus pourri que ce qu'on trouve en général dans les bouquins de Lycée et qui fait (justement) que les gamins ne comprennent rien à l'importance du vocabulaire en mathématique : pour la majorité, les mots qu'on utilise n'ont aucune importance, les maths, c'est juste du calcul (**)
- Par contre le "Trouver le lieu des points par où passent deux droites D confondues" il est on ne peut plus clairement "sans queue ni tête" : est-ce que ça viendrait à l'esprit de qui que ce soit (de sain d'esprit) de dire que "dans mon panier il y a deux pommes confondues" ? Et est ce que tu crois vraiment que, si quelqu'un devant toi prononçait une telle phrase, tu n'aurait aucun doute concernant le sens de la phrase ?
Bref, concernant une telle formulation, tout ce que je peut te dire, c'est que si je trouvait ça dans une copie d'élève, je l'entourerais en rouge et j'écrirais "relisez vous !!!!"
(*) Vu ce que je constate de la compréhension qu'ils ont du vocabulaire mathématique à l'issue du bac.
(**) Et c'est en grande partie du fait que dans les bouquins on trouve régulièrement un tel charabia sans queue ni tête que les gamins en déduisent que la partie "texte", c'est poubelle direct. Et bien sûr eux ne mettent jamais de texte vu qu'ils se sentent bien incapable (à juste titre) de reproduire un tel charabia.
P.S. Et pour continuer sur le même thème, admettons que tu ais en face de toi un élève venant d'un système autre que Français (ce qui arrive évidement souvent à la fac) et qui n'a donc pas l'habitude de rencontrer un tel charabia. Cet élève là, forcément, il va te demander pourquoi la question est formulé sous la forme opaque "Trouver le lieu des points par où passent deux droites D confondues" plutôt que la forme claire (et plus courte) "Déterminer les points par lesquels passent une seule droite D". Tu lui répond quoi ?
Bon, pour commencer et pour éviter de me faire traiter de "gamin incompétent" comme d'autres, je précise que j'ai 53 ans et que je suis prof. (de math) à la fac.posso49 a écrit:...et suis d'accord avec lui pour dire que le libellé de cet exercice est correct, même s'il est un peu déroutant.
Ensuite, concernant l'énoncé, non, il n'est absolument pas "correct" :
- Déjà la phrase "Par un point donné passent en général deux droites" devrait évidement être précédée de "On admet que" ou bien "Démontrer que".
- Ensuite, dans cette même phrase, je suis certain (*) que pour plus de la moitié des élèves de terminale le sens du "en général" va être mal compris.
Jusque là, c'est pas super gênant et c'est pas plus pourri que ce qu'on trouve en général dans les bouquins de Lycée et qui fait (justement) que les gamins ne comprennent rien à l'importance du vocabulaire en mathématique : pour la majorité, les mots qu'on utilise n'ont aucune importance, les maths, c'est juste du calcul (**)
- Par contre le "Trouver le lieu des points par où passent deux droites D confondues" il est on ne peut plus clairement "sans queue ni tête" : est-ce que ça viendrait à l'esprit de qui que ce soit (de sain d'esprit) de dire que "dans mon panier il y a deux pommes confondues" ? Et est ce que tu crois vraiment que, si quelqu'un devant toi prononçait une telle phrase, tu n'aurait aucun doute concernant le sens de la phrase ?
Bref, concernant une telle formulation, tout ce que je peut te dire, c'est que si je trouvait ça dans une copie d'élève, je l'entourerais en rouge et j'écrirais "relisez vous !!!!"
(*) Vu ce que je constate de la compréhension qu'ils ont du vocabulaire mathématique à l'issue du bac.
(**) Et c'est en grande partie du fait que dans les bouquins on trouve régulièrement un tel charabia sans queue ni tête que les gamins en déduisent que la partie "texte", c'est poubelle direct. Et bien sûr eux ne mettent jamais de texte vu qu'ils se sentent bien incapable (à juste titre) de reproduire un tel charabia.
P.S. Et pour continuer sur le même thème, admettons que tu ais en face de toi un élève venant d'un système autre que Français (ce qui arrive évidement souvent à la fac) et qui n'a donc pas l'habitude de rencontrer un tel charabia. Cet élève là, forcément, il va te demander pourquoi la question est formulé sous la forme opaque "Trouver le lieu des points par où passent deux droites D confondues" plutôt que la forme claire (et plus courte) "Déterminer les points par lesquels passent une seule droite D". Tu lui répond quoi ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation de droite
Salut Ben314,
"Il s'agit de l'exercice 734 de Géométrie 1ere C de Lebossé Hémery version 1966"
donc un vieux livre!
ah c'était pas mieux avant alors?
"Il s'agit de l'exercice 734 de Géométrie 1ere C de Lebossé Hémery version 1966"
donc un vieux livre!
ah c'était pas mieux avant alors?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
97 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
