Equation de droite

[Pseuda]

Bonjour,

"Trouver le lieu des points" : c'est très courant, se voit beaucoup dans les exercices de TS sur les complexes, mais aussi en 2nde sur des exos de géométrie, etc ...

Donc, il n'y aurait que moi qui aurait compris cet énoncé du 1er coup, cela me flatte !

[beagle]

Bonjour,

"Trouver le lieu des points" : c'est très courant, se voit beaucoup dans les exercices de TS sur les complexes, mais aussi en 2nde sur des exos de géométrie, etc ...

Donc, il n'y aurait que moi qui aurait compris cet énoncé du 1er coup, cela me flatte !

C'est à double tranchant Pseuda, fais gaffe,
si c'est un livre de 1966
et que tu sais lire le vieux français ...

[Pseuda]

C'est à double tranchant Pseuda, fais gaffe,
si c'est un livre de 1966
et que tu sais lire le vieux français ...

Les maths sont les maths, elles ne bougent pas en principe ... et il faut savoir s'adapter ...

Et d'abord, c'est pas du "vieux français", c'est du "français". Le vieux français, c'est les poèmes de François Villon...

N'importe quoi comme d'habitude.

Et j'en resterai là dans cette discussion stérile depuis le début.

Mais je remarquerais pour moi, que je suis apparemment la seule professeur de collège / lycée parmi les protagonistes de cette discussion, avec posso49, donc je sais de quoi je parle.

Et @aviateur, il n'y a pas de mal à ne pas avoir compris du 1er coup l'énoncé de cet exercice.

Et en dernier lieu, le poseur de la question a obtenu satisfaction avec la réponse que je lui ai apportée, et il n'y a que cela qui compte en définitive, parce que c'est quand même le seul but de l'entraide mathématique, pas de perdre son temps dans de vaines polémiques, déclenchées une fois de plus par @Ben314, soit dit en passant.

[beagle]

et la question est : trouver x
alors l'élève entoure x et écrit: "il est là"!
J'adore.

[aviateur]

Franchement @pseuda
@pseuda a dit:
"Et @aviateur, il n'y a pas de mal à ne pas avoir compris du 1er coup l'énoncé de cet exercice."
Je te respecte mais je n'ai vraiment pas l'impression que tu comprends que à aucun moment je n'ai chercher à polémiquer et je ne vois pas non plus en quoi @ben aurait déclenché de vaines polémiques.
En particulier, relativement à ce que tu dis ci-dessus, il faut arrêter de faire dire au gens ce qu'ils n'ont pas dit.
Donc à ce niveau de conversation je préfère que cela s'arrête ici.

[Black Jack]

Bonjou

On peut montrer sans trop de difficulté que toutes les droites D qui existent sont tangentes au cercle d'équation (x-2)²+(y-1)² = 1

@Black Jack D'accord c'est la clé essentielle de ta démonstration et donc tu
peux expliquer comment tu trouves cela?

Soit le système :

(x-2)²+(y-1)² = 1
(1 - m²)x + 2my = -m² + 2m + 3

Si m diff de -1 ou 1 :

x = (-m² + 2m + 3 - 2my)/(1-m²)

((-m² + 2m + 3 - 2my)/(1-m²) - 2)² + (y-1)² = 1

Qu'on développe, on arrange ... on a une équation du second degré en y.

On calcule le discriminant de cette équation ... et on trouve qu'il est nul quelle que soit la valeur de m (différente de -1 ou 1)

Donc pour chaque valeur de m, la droite D correspondante a un seul point de rencontre avec le cercle d'équation (x-2)²+(y-1)² = 1.

Chaque droite D est tangente au cercle d'équation (x-2)²+(y-1)² = 1

On traite les cas m = -1 ou 1 à part ... (trivial)

[aviateur]

@BlackJack
ça ne va toujours pas ta démonstration. En effet tu dis "chaque droite D qui existent sont tangentes au cercle...."
Déjà si je traduis cela en bon français, tu as surement voulu dire que si deux droites de la famille sont perpendiculaires alors elles sont tangentes au cercle C (celui de la question 1)
Donc tu prends une droite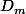 "solution" et pour un point (x,y) quelconque de cette droite
tu exprimes x en fonction de y et m. Et puis tu remplace dans l'équation du cercle C x et y et puis tu continues.
Cela signifie que tu supposes que la droite "solution" passe par le cercle.
Et bien cela ne répond en rien à la question. En effet si je considère deux droites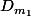 et perpendiculaires (s'il en existe, et il en existe puisque je l'ai montré; mais a priori on n'utilise ma démo, n-est ce pas?) je ne vois pas en quoi si pour l'une quelconque des 2 tu peux te permettre de dire qu'elle a un point commun avec le cercle.

[nodgim]

On considère dans un repère orthonormé la droite d'équation (1-m²)x+2my+m²-2m-3=0. Par un point donné passent en général deux droites.

Précisément, c'est la phrase en rouge qui m'a troublé. Car par un point donné passent, en général, une infinité de droite.
Après, je comprends bien que, sans doute, il doit passer 2 points de la droite paramétrée en question.

Sinon, le lieu d'un point, c'est clair pour moi.

[Black Jack]

ça ne va toujours pas ta démonstration. En effet tu dis "chaque droite D qui existent sont tangentes au cercle...."
Déjà si je traduis cela en bon français, tu as surement voulu dire que si deux droites de la famille sont perpendiculaires alors elles sont tangentes au cercle C (celui de la question 1)

Pas du tout.
Ce que j'ai dit est que n'importe quelle droite D est tangente au cercle.

Puisque tu es si fort pour critiquer les autres surtout quand tu ne comprends pas, trouve donc une droite D (donc une valeur de m) telle que la droite D correspondante ne serait pas tangente au cercle que j'ai indiqué.

Au lieu de critiquer, tu ferais mieux de ne pas te prendre pour le messie et te dire que d'autres peuvent aussi avoir raison... même si tu ne comprends pas pourquoi.

Et si tu n'es toujours pas capable de comprendre, trace donc le cercle que j'ai indiqué avec un logiciel quelconque et une droite D en laissant m en paramètre que tu feras varier ... et constate.

Quand l'évidence te frappera ... alors peut-être seras-tu capable de comprendre ce que j'ai démontré. (n'importe quelle droite D (qui existe) est tangente au cercle.)

Et si tu veux relever les fautes d'orthographe ou de syntaxe, je te propose de le faire sur les messages de quelqu'un que tu as loué dans ce post ...

[Black Jack]

ça ne va toujours pas ta démonstration. En effet tu dis "chaque droite D qui existent sont tangentes au cercle...."
Déjà si je traduis cela en bon français, tu as surement voulu dire que si deux droites de la famille sont perpendiculaires alors elles sont tangentes au cercle C (celui de la question 1)

Pas du tout.
Ce que j'ai dit est que n'importe quelle droite D est tangente au cercle.

Puisque tu es si fort pour critiquer les autres surtout quand tu ne comprends pas, trouve donc une droite D (donc une valeur de m) telle que la droite D correspondante ne serait pas tangente au cercle que j'ai indiqué.

Au lieu de critiquer, tu ferais mieux de ne pas te prendre pour le messie et te dire que d'autres peuvent aussi avoir raison... même si tu ne comprends pas pourquoi.

Et si tu n'es toujours pas capable de comprendre, trace donc le cercle que j'ai indiqué avec un logiciel quelconque et une droite D en laissant m en paramètre que tu feras varier ... et constate.

Quand l'évidence te frappera ... alors peut-être seras-tu capable de comprendre ce que j'ai démontré. (n'importe quelle droite D (qui existe) est tangente au cercle.)

Et si tu veux relever les fautes d'orthographe ou de syntaxe, je te propose de le faire sur les messages de quelqu'un que tu as loué dans ce topic ...

[aviateur]

Bonjour
Reste poli s'il te plait. On est en droit de ne pas comprendre ce que tu dis parce que c'est mal dit. Et je ne me prend pas plus fort qu'un autre sauf qu'une démonstration pour qu'elle soit acceptable ou compréhensible il faut qu'elle soit comprise.
Tu fais une démonstration différente et j'y ne vois aucun problème.
Donc à la lecture je ne comprends pas bien mais tu viens de corriger.
Déjà c'est un fait, je comprend mieux ce que tu a voulu dire.
Maintenant est-ce vrai où est ce faux? ce n'est pas à moi de le dire, c'est toi qui fait la démonstration.
Avec un logiciel tu peux faire une conjecture si c'est bon ou non. Si cela te semble bon, s'il te plait tant que tu ne l'a pas démontré ta démonstration n'est pas bonne.
Dire à quelqu'un que ça démonstration n'est pas claire ou pas bonne ça conduit à quoi maintenant?

[aviateur]

@BlackJack Je relis en détail tes "attaques."Je crois vraiment que tu ne comprends pas ce que je dis.
Effectivement on fait des fautes d'orthographes. En première écriture j'en fais et je corrige toujours le maximum car moi même ça me gêne un peu d'en voir trop.
Mais si tu fais une démonstration et si tes phrases sont trop alambiquées (et ne pas confondre avec des fautes d'orthographe) a un tel point que l'on ne comprend pas bien la démo. C'est normal de demander d'être plus clair. Maintenant après cela si on voit que la démonstration n'est pas bonne ou bien si il manque une part importante, c'est normal de le dire.
Je ne vois pas en quoi, en retour, on se retrouve avec des réponses comme ici.

[aviateur]

@Black Jack, bon à la relecture on finit par comprendre (modulo les calculs que j'accepte).
Mais la première fois tu dis qu'il n'y a pas de droites perpendiculaires.
Je te fais remarquer que non.
La deuxième fois tu dis qu'il est facile de voir... pour donner les solutions. Oui, mais montre le (c'est normal non?)
Finalement tu fais effectivement une démo relativement facile mais pardon il faut s'y prendre à plusieurs reprise pour comprendre.
Je suis désolé d'insister grossièrement mais dans une démo il y a un minimum a bien dire les choses.

[Black Jack]

Aviateur

Quand tu ne comprends pas, tu modifies le texte écrit par d'autres et tu relèves les incohérences dans ce que tu penses avoir compris ... alors que tu es loin du compte. (j'exclus de là ma toute première réponse pour la question 2 ... malgré que j'avais clairement ecrit que rien n'était vérifié).

C'est énervant, surtout que les remarques sont faites par des "la démonstration est fausse ou ne va toujours pas ou ... ce que tu dis est mal dit ou ...)

L'ébauche de la démo que j'ai faite (après demande car pour moi cela pouvait être fait avec les connaissances de Seconde et donc fait par le questionneur si il le voulait) est suffisante et permet de conclure que :
"N'importe quelle droite D est tangente au cercle d'équation (x-2)² + (y-1)² = 1"
Et puis ensuite se servir de ce résultat pour répondre facilement à la question 2.

Evidemment si cela dépasse les compétences de l'un ou l'autre de savoir démonter que chaque droite d'une famille connue de droites (dépendant d'un paramètre) est tangente à un cercle dont on connait l'équation, et de ne pas comprendre malgré une aide non négligeable sur une manière possible de procéder, alors ... il vaut mieux laisser tomber.

La question (la vraie) à se poser est comment avoir eu l'idée que "N'importe quelle droite D est tangente au cercle d'équation (x-2)² + (y-1)² = 1", mais vu la difficulté déjà rencontrée jusqu'ici pour des broutilles, il vaut mieux ne pas tenter le diable.

EDIT :
Pas vu ta réponse précédente avant d'envoyer celle-ci.

[aviateur]

Bon, je vais m'arrêter après cela car je n'en peux plus.
Je n'aime pas me vanter et je ne veux pas étaler ici quoique ce soit de privé. Mais simplement sur ce forum quiconque aura pu voir les types de problèmes que j'ai résolus pour aider X ou Y, rira de ce qu'il y a ci-dessous.
S'il te plait toi (et autres), au minimum évitez ce genre de bassesses récurrentes qui vous enfoncent:

Evidemment si cela dépasse les compétences de l'un ou l'autre de savoir démonter que chaque droite d'une famille connue de droites (dépendant d'un paramètre) est tangente à un cercle dont on connait l'équation, et de ne pas comprendre malgré une aide non négligeable sur une manière possible de procéder, alors ... il vaut mieux laisser tomber.

Au demeurant, c'est à l'image dont vous faites des raisonnements mathématiques.
Le bouquet est atteint aujourd'hui sur ce post!

[Black Jack]

"Au demeurant, c'est à l'image dont vous faites des raisonnements mathématiques. "

Ben oui, voila.
Mes raisonnements sont mauvais paraît-il ... mais j'avais compris l'énoncé.

[aviateur]

C'est bien, tu sais lire le charabia! Mais moi je ne trouve pas de smileys qui me fait pleurer sur l'avenir des maths.

[Lostounet]

Bonjour à tous,

Dommage que la discussion - qui aurait pu déboucher sur un dialogue mathématique constructif - se soit transformée en attaques personnelles virulentes.

Je tiens à rappeler que nous sommes tous là sur ce forum pour échanger, chacun selon ses intérêts et son niveau. On ne doit donc pas s'attendre toujours et systématiquement à des réponses exhaustives et abouties de la part de chaque intervenant/intervention.

Mais on doit quand même s'attendre à une volonté d'échanger avec l'autre même en cas de désaccord...et dans le respect de chacun et de son expérience.

Les attaques personnelles ne sont pas nécessaires: je vous prie de revenir au sujet de départ qui propose quand même quelque chose d'intéressant.

Je n'hésiterai pas à fermer (à regret) la discussion à l'avenir si les choses ne s'améliorent pas...

[aviateur]

@Lostounet
Je préfère que tu fermes le post de suite.
Il y a des limites à ne pas dépasser et elles le sont depuis le début de ce post!

J'en ai ma claque de ma claque. Je me suis tapé l'autre jour le génie de @Cami qui a démontré
la conjecture du problème 3x+1.
Ici le @posso49, qui je pensais avait 15ans, m'affirme que l'énoncé est tel quel dans un bouquin avec toute la clique derrière qui se jette derrière lui pour dire qu'on est con si on ne sait lire un énoncé merdique.

[Lostounet]

@Lostounet
Je préfère que tu fermes le post de suite.
Il y a des limites à ne pas dépasser et elles le sont depuis le début de ce post!

Ne peut-on pas espérer que la discussion change de direction ? Afin de se mettre d'accord sur une (re)formulation de l'énoncé de départ qui soit claire pour tous et afin de voir si l'auteur a bien reçu réponse à sa question..?

Je n'ai malheureusement pas pu lire tous les messages depuis le début...donc s'il y a quelque chose que je devrais savoir, merci de me le dire par MP, aviateur.