Bonjour,
Je souhaiterai calculer L en fonction du rayon r afin d'avoir une surface d'intersection moitié de la surface du cercle C1.
L'image jointe explique mon problème
Intersection de deux cercles
9 messages
- Page 1 sur 1
Re: Intersection de deux cercles
Salut,
Si O désigne le centre de C1, A et B les points d'intersections des deux cercles et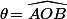 (en radians bien sûr) alors on montre facilement que l'aire de l'intersection est
(en radians bien sûr) alors on montre facilement que l'aire de l'intersection est \big)) (en écrivant que la moitié de cette aire est constitué d'une "part de camembert" privé d'un triangle isocèle dont on sait calculer les aires).
(en écrivant que la moitié de cette aire est constitué d'une "part de camembert" privé d'un triangle isocèle dont on sait calculer les aires).
Résoudre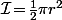 revient à résoudre
revient à résoudre \!=\!\frac{\pi}{2}) qu'on ne sait pas résoudre à l'aide des fonctions usuelles, mais on peut approximer facilement la solution (tracé de courbe ou autre méthode) :
qu'on ne sait pas résoudre à l'aide des fonctions usuelles, mais on peut approximer facilement la solution (tracé de courbe ou autre méthode) : 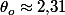 radians.
radians.
Ensuite, la distance entre les deux centres est systématiquement égale à) ce qui, dans le cas où
ce qui, dans le cas où 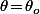 donne
donne 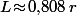 (si tu veut plus de précision, prend 0,8079455066)
(si tu veut plus de précision, prend 0,8079455066)
Si O désigne le centre de C1, A et B les points d'intersections des deux cercles et
Résoudre
Ensuite, la distance entre les deux centres est systématiquement égale à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection de deux cercles
J'ai effectivement mal regardé le dessin.
Ce que je calcule dans mon précédent post. (et c'est d'ailleurs écrit en noir sur blanc), c'est la distance D entre les centre des deux cercles.
Alors que le L du dessin, c'est L=2R-D
Ce que je calcule dans mon précédent post. (et c'est d'ailleurs écrit en noir sur blanc), c'est la distance D entre les centre des deux cercles.
Alors que le L du dessin, c'est L=2R-D
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection de deux cercles
@chan79: comment as tu trouvés 1,192 stp ? est-ce comme le développement de Ben314 ? car je ne voie pas le triangle isocèle
peut etre il faudrait calculer la somme des aires 1, 2 et 3
peut etre il faudrait calculer la somme des aires 1, 2 et 3
- Fichiers joints
-
- cercle.png (20.25 Kio) Vu 1577 fois
Re: Intersection de deux cercles
Le truc en rose sur ton dessin, c'est la "part de camembert" qui a pour aire 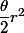 .
.
Le triangle isocèle OAB a pour aire}{2}r^2) .
.
Et si tu regarde la part de camembert privé du triangle, ça fait exactement la moitié de l'intersection des deux cercles.
Le triangle isocèle OAB a pour aire
Et si tu regarde la part de camembert privé du triangle, ça fait exactement la moitié de l'intersection des deux cercles.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intersection de deux cercles
qwerty213 a écrit:@chan79: comment as tu trouvés 1,192 stp ?
J'ai fait comme Ben314; je le mets quand même.
L'aire de l'intersection des deux disques est égale au double de l'aire du secteur OAB diminué de l'aire du losange (on suppose que les deux cercles ont le même rayon)
soit
La distance entre les deux centres est donc
puis
- Fichiers joints
-
- img.jpg (20.09 Kio) Vu 1553 fois
Re: Intersection de deux cercles
la solution finale ne devrait pas être linaire, mais plutôt en fonction de R² ou quelque chose de ce genre
Re: Intersection de deux cercles
Donc si je comprend bien, ce que te dicte ton intuition, c'est que, si R est exprimé en mètres, alors L est en mètres carrés.qwerty213 a écrit:la solution finale ne devrait pas être linaire, mais plutôt en fonction de R² ou quelque chose de ce genre
Perso, la mienne, c'est pas ça qu'elle me dit...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
