Déterminer sans machine deux entiers naturels
Déterminer deux entiers naturels
15 messages
- Page 1 sur 1
Déterminer deux entiers naturels
Bonjour,
Déterminer sans machine deux entiers naturels et
et  tels que :
tels que :
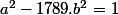
Déterminer sans machine deux entiers naturels
Re: Déterminer deux entiers naturels
Et si on veut des entiers naturels strictement positifs, avec une très grande feuille de papier et beaucoup de patience et de soin, on calcule à la main le développement en fraction continue de 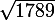 jusqu'à repérer sa période (67). Il ne reste plus alors qu'à calculer la réduite d'ordre 2x67 - 1 = 133 pour obtenir la solution
jusqu'à repérer sa période (67). Il ne reste plus alors qu'à calculer la réduite d'ordre 2x67 - 1 = 133 pour obtenir la solution
a=13673687937600285436522338047798889300505982960692087\
644059539022368201
b=323281233024712565221770716009156212819348235266978239\
649677477568260
En période de confinement, ça occupe !
a=13673687937600285436522338047798889300505982960692087\
644059539022368201
b=323281233024712565221770716009156212819348235266978239\
649677477568260
En période de confinement, ça occupe !
Re: Déterminer deux entiers naturels
En période de confinement, on peut au moins se permettre de chercher deux entiers naturels non nuls et de ne pas utiliser le développement en fraction continue bien évidemment 
Re: Déterminer deux entiers naturels
Et comment les cherches-tu ?
En as-tu des plus petits que ceux que j'ai donnés ?
En as-tu des plus petits que ceux que j'ai donnés ?
Re: Déterminer deux entiers naturels
En développant : ^6}{64})^{2})
Vous obtiendrez une somme de la forme :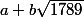 ou
ou  et
et  sont deux entiers solution.
sont deux entiers solution.
Vous obtiendrez une somme de la forme :
Modifié en dernier par anthony_unac le 24 Avr 2020, 21:33, modifié 1 fois.
Re: Déterminer deux entiers naturels
Re: Déterminer deux entiers naturels
anthony_unac a écrit:En développant :
Vous obtiendrez une somme de la forme :ou
et
sont les deux entiers solution.
Pas LES deux entiers solutions, mais UN couple d'entiers solution (il y a une infinité de tels couples). Les entiers que tu obtiens (tu n'expliques pas comment) sont de taille à peu près deux fois plus grande que les entiers dans la solution que j'ai donnée ; ils correspondent à la réduite d'ordre 267 de la fraction continue. Ton
Regardons de plus près le nombre
que tu élèves à la puissance 12 pour trouver ta solution. C'est aussi une unité de l'anneau des entiers du corps quadratique
Au lieu d'élever cette unité à la puissance 12, tu aurais pu te contenter de l'élever à la puissance 6. Tu serais alors retombé sur la solution que j'ai donnée (correspondant à la réduite d'ordre 133). Et si tu l'avais élevée seulement à la puissance 3, tu aurais trouvé la plus petite solution en entiers >0 de
Re: Déterminer deux entiers naturels
GaBuZoMeu a écrit:anthony_unac a écrit:En développant :
Au lieu d'élever cette unité à la puissance 12, tu aurais pu te contenter de l'élever à la puissance 6. Tu serais alors retombé sur la solution que j'ai donnée (correspondant à la réduite d'ordre 133).
Pourrais tu m'expliquer comment tu peux savoir à l'avance qu'il faut élever le bousin à la puissance 6 ?
Je serais curieux également de voir ton calcul pas à pas qui exploite le développement en fraction continu
Re: Déterminer deux entiers naturels
Ta feuille écrite en bleu est difficilement lisible. Mais on y voit tout de même clairement ce que tu fais : des calculs de développement en fraction continue.
Tu peux voir cette page wikipedia (je pense que tu l'as déjà vue, mais peut-etre n'es-tu pas allé jusqu'à la section sur les fractions continues ?)
Tu peux voir cette page wikipedia (je pense que tu l'as déjà vue, mais peut-etre n'es-tu pas allé jusqu'à la section sur les fractions continues ?)
Re: Déterminer deux entiers naturels
La page wiki que tu donnes est précisément la méthode que j'utilise avec les mêmes notations.
La petite subtilité de la méthode de Chakravala réside dans le fait qu'on ne s'enquiquine pas à calculer tous les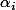 . Dès que l'on tombe sur une norme valant +-1 ou +-2 ou +-4, la méthode vous donne UNE solution. Dans cet exemple précis, il a fallu pousser le calcul jusqu'à
. Dès que l'on tombe sur une norme valant +-1 ou +-2 ou +-4, la méthode vous donne UNE solution. Dans cet exemple précis, il a fallu pousser le calcul jusqu'à 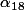 .
.
En poussant les calculs jusqu'à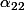 , on observe également que le cube de sa norme (
, on observe également que le cube de sa norme (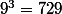 )vaut précisément le carré de la norme de
)vaut précisément le carré de la norme de 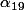 (
(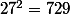 ).
).
On peut alors conclure que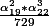 est solution :
est solution :
)^2*(1683174008788325+39794572718012\sqrt(1789))^3)/729) =
=
 + 13673687937600285436522338047798889300505982960692087644059539022368201)
Cela correspond précisément à la solution que tu donnes (sans avoir fourni tes étapes de calcul pas à pas).
La petite subtilité de la méthode de Chakravala réside dans le fait qu'on ne s'enquiquine pas à calculer tous les
En poussant les calculs jusqu'à
On peut alors conclure que
Cela correspond précisément à la solution que tu donnes (sans avoir fourni tes étapes de calcul pas à pas).
Re: Déterminer deux entiers naturels
Je te l'ai indiqué : je calcule le développement en fraction continue. C'est en fait ce que tu fais aussi - sans le savoir ; bon tu raccourcis un peu en prenant à chaque fois l'entier le plus proche au lieu de prendre la partie entière pour le développement classique. On peut effectivement s'arrêter dès qu'on trouve une norme égale à plus ou moins 4 parce qu'on a attrapé une unité qui est la moitié du 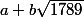 courant (1789 est congru à 1 modulo 4). On explore alors les puissances de cette unité, on voit que son cube fournit une solution entière à l'équation avec
courant (1789 est congru à 1 modulo 4). On explore alors les puissances de cette unité, on voit que son cube fournit une solution entière à l'équation avec  , et donc sa puissance 6e sera une solution entière à l'équation avec
, et donc sa puissance 6e sera une solution entière à l'équation avec  .
.
Re: Déterminer deux entiers naturels
Une bonne question du coup est de savoir quand l'apparition d'une norme égale à 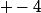 ou
ou 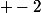 apparaîtra.
apparaîtra.
Ou plus généralement quand pouvons nous trouver un couple solution de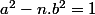 partant d'un entier
partant d'un entier  donné.
donné.
En première observation, il semblerait que l'arrêt se produise vers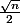
Si on s’intéresse par exemple à l'équation :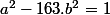 , on estime qu'il faudra pousser le calcul jusqu’à
, on estime qu'il faudra pousser le calcul jusqu’à 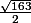 soit environ
soit environ 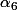 et c'est ce qu'on trouve en pratique. Il était même possible de conclure dès l'obtention de
et c'est ce qu'on trouve en pratique. Il était même possible de conclure dès l'obtention de 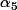 en remarquant que la norme de
en remarquant que la norme de 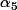 élevé au carré est égale à la norme de
élevé au carré est égale à la norme de 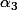 :
:

Si on s’intéresse à présent à l'équation :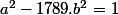 , on estime qu'il faudra pousser le calcul jusqu’à
, on estime qu'il faudra pousser le calcul jusqu’à 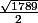 soit environ
soit environ  et en pratique, une norme égale à
et en pratique, une norme égale à 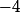 arrive dès
arrive dès 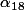 .
.
Ou plus généralement quand pouvons nous trouver un couple solution de
En première observation, il semblerait que l'arrêt se produise vers
Si on s’intéresse par exemple à l'équation :

Si on s’intéresse à présent à l'équation :
Re: Déterminer deux entiers naturels
Tes scans sont très difficilement lisibles. J'y renonce.
9a irait peut-être mieux si tu utilisais un stylo noir.
9a irait peut-être mieux si tu utilisais un stylo noir.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :



