Urne et Boules (à nouveau)

[Rouvire]

Bonjour,
Une urne contient 3 types de boules, A, B, C. Il y a au moins une boule A, une B et une C dans l'urne. Il y a 3 joueurs A, B, C.
Le premier joueur A tire une boule, si c'est une boule de type A il a "gagné" et la partie s'arrête, sinon la boule qu'il a tiré est enlevée de l'urne et la partie continue.
Le deuxième joueur B tire alors une boule, si c'est une boule B c'est lui qui a "gagné" et la partie s'arrête, sinon la boule qu'il a tiré est enlevée de l'urne et la partie continue.
Le troisième joueur C tire alors une boule, si c'est une boule C c'est lui qui a "gagné" et la partie s'arrête, sinon la partie est déclarée nulle.

Par exemple avec 3 boules (une A, une B et une C)
La probabilité qu'a A de "gagner" est 1/3
Celle de B est 1/3 * 1/2 = 1/6
Celle de C est aussi 1/3 * 1/2 = 1/6
Celle que la partie soit nulles est (1/3 * 1/2) + (1/3 * 1/2) = 2/6

(On a bien (1/3 + 1/6 +1/6 + 2/6) = 1

La question est: Combien de boules A, B, C il faut mettre dans l'urne pour que la probabilité de "gagner" de chaque joueur soit la même.

A mon avis c'est impossible de rendre la partie équitable, mais quel raisonnement ou démonstration? ou alors quel contre exemple?

Merci.

[GaBuZoMeu]

Bonsoir,
Je te suggère de nommer les nombres de boules 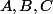et de faire un arbre où tu feras figurer toutes les histoires possibles, avec les probabilités calculées en fonction de à chaque embranchement.

[Rouvire]

Ok, merci Gabuzome de t’intéresser à ce sujet. Je ne vois pas comment débuter l’arbre dont tu parles mais je vais te montrer comment j’avais commencé à étudier ce problème (avec tes notations).

On pose n=a+b+c. On tire toutes les boules de l’urne. Le nombre total de suites qu’on peut obtenir est n! / (a!b!c!)

Le nombre de suites "A" où c'est une boule A qui est tirée en premier est a(n-1)! / (a!b!c!)
Le nombre de suites "B" (BB ou CB) est (b²-b+bc)(n-2)! / (a!b!c!)
Le nombre de suites "C" (BAC ou BCC ou CAC ou CCC) est (c^3+c²(a+b-3)+c(ab-a-b+2))(n-3)! / (a!b!c!)
Le nombre de suite où la partie est nulle est (a²b+a²c+ab²+b²c+ac²+bc²+2abc-2ab-2ac-2bc)(n-3)! / (a!b!c!)

On calcule l’équation pour que le nombre de suites "A" soit le tiers du nombre de suites où la partie n'est pas nulle.
-2a^3+b^3+c^3-4a²b-4a²c+6a²-ab²+2b²c-3b²-ac²+2bc²-3c²-2abc+5ab+5ac-4bc-4a+2b+2c = 0

On calcule l’équation pour que le nombre de suites "B" soit le tiers du nombre de suites où la partie n'est pas nulle.
a^3-2b^3+c^3+2a²b+2a²c-3a²-ab²-4b²c+6b²+2ac²-bc²-3c²+abc-ab-4ac+5bc+2a-4b+2c = 0

On arrive alors à
-a^3-b^3-6a²b-6a²c+9a²+6b²c-9b²-3ac²+3bc²-3abc+6ab+9ac-9bc-6a+6b = 0

Voila, j’espère que je ne me suis pas trompé dans les calculs et de toute façon là je bloque sur cette équation diophantienne.

Remarque. On peut écrire un programme qui part de a=1, b=1 et c=1 et avec un dénombrement des suites.
DEB:
Si A = B = C alors STOP
Si C <= A et C <= B alors c = c+1
Si B <= A et B < C alors b = b + 1
Si A < Pb et A < Pc alors a = a + 1
GOTO DEB

C’est le problème de savoir si un programme a une fin ou pas.

Ce qui est "marrant" dans ce "jeu" c’est qu’il a des solutions pour 2 joueurs mais qu’apparemment il n’en n’a plus pour 3, 4, 5, … (un peu comme Fermat)

[GaBuZoMeu]

L'arbre est simple : au premier tirage, 3 possibilités A, B et C. Si A ça s'arrête, gagnant pour A. Partant de chacun des noeuds B et C trois branches A, B, C. On s'arrête pour les noeuds BB et CB, gagnants pour B. Partant de chacun des noeuds BA, BC., CA, CC de nouveau trois branches A, B, C. On s'arrête pour les noeuds BAC, BCC, CAC, CCC gagnants pour C. Les probabilités dans l'arbre sont faciles à calculer, et on aboutit (si personne ne s'est trompé) aux mêmes équations.

[Rouvire]

Merci GaBuZoMeu (bien orthographié).
Bon, je n'ai aucune idée de comment on traite une équation diophantienne de ce type (c'est bien au dessus de mon niveau de math qui est Bac C de 1972 )
Si on reprend la comparaison avec Fermat, pour 2 joueurs la suite des couples (a,b) qui marchent est:
(1,2); (6,10); (40, 65); (273, 442); (1870, 3026); (12816, 20737); …
La suite des différences b-a donne des carrés parfaits
1² ; 2² ; 5² ; 13² ; 34² ; 89² ; …
La suite des rapports a/ (b-a)^1/2 donne
1; 3; 8; 21; 55; 144; …
Si on combine ces 2 suites on obtient
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; … La suite de Fibonacci

Dans la suite des triplets de Pythagore a²+b²=c² on peut aussi faire apparaitre cette suite

[catamat]

Bonjour

Le problème semble ne pas avoir de solution exacte, mais on peut trouver de bonnes valeurs approchées, c'est à dire des nombres a, b et c pour lesquels les trois probas sont presque égales.

Par ex : a=3, b=4 et c=6

p(A)=3/13 soit environ 0.2308
p(B)=
p(C)=

Voilà, sauf erreur, on a donc les deux premières décimales correctes. Mais Il y a surement mieux en augmentant les valeurs de a, b et c.

[Rouvire]

Bonjour,

Oui catamat, il n'y a probablement pas de solution exacte.

Si on reprend le programme (algorithme) ci dessous.

DEB:
Si A = B = C alors STOP
Si C <= A et C <= B alors c = c+1
Si B <= A et B < C alors b = b + 1
Si A < B et A < C alors a = a + 1
GOTO DEB

Je pense que s'il y a une solution exacte il ne peut pas la rater.
Mais s'il n'y en a pas il boucle (il ne s'arrête jamais).
Je suis allé jusqu'à: a=960, b=1259 et c=1827.
On a alors les probabilités (si je ne me suis pas trompé)
Pa = 0,237271379
Pb = 0,237321177
Pc = 0,237206726
Pnulle = 0,288200718

Peut-être que ces probabilités limites correspondent à des constantes connues.

Merci