Bonjour,
1) Le jeu avec 2 joueurs:
On a 2 joueurs A et B. On met a boules de type "A" dans une urne et b boules de type "B" . Le premier joueur à jouer est A, il tire au hasard une boule de l'urne, si c'est une boule de type "A" il a gagné et la partie s'arrête, sinon le joueur B tire à son tour une boule et si c'est une boule de type "B" c'est lui qui à gagné, sinon la partie est nulle. On cherche à savoir combien de boules a et b il faut mettre dans l'urne pour que la partie soit équitable dans les 2 cas suivants (avec remise ou sans remise).
- Avec remise (quand A remet la boule qu'il a tirée dans l'urne): on ne peut pas trouver de nombre a et b tel que la partie soit équitable.
- Sans remise (A garde la boule qu'il a tirée): on peut trouver une infinité de couples de nombres (a,b) tel que la partie soit équitable. Exemples (1,2) (6,10) (40,65) ...
2) Le jeu avec 3 joueurs:
On a 3 joueurs A, B et C qui jouent dans cet ordre avec 3 types de boules "A", "B" et "C" dans l'urne et la même règle (si A tire une boule "A" il a gagné et la partie s'arrête, sinon c'est à B de jouer et si il tire une boule "B" il a gagné sinon ...). On cherche maintenant les triplets (a,b,c) de nombre de boules à mettre dans l'urne pour que la partie soit équitable pour les 3 joueurs.
- Avec remise (A et B s'ils n'ont pas gagné doivent remettre la boule tirée dans l'urne): on ne peut pas trouver de triplet (a,b,c) pour que la partie soit équitable.
- Sans remise (A et B gardent les boules qu'ils ont tirées): je pense alors qu'on ne peut pas trouver de triplet (a,b,c) pour que la partie soit équitable. Est-ce-qu'il y a une démonstration pour ce cas?
Boules Urne et Jeu
7 messages
- Page 1 sur 1
Salut,
Après quelques calculs, il me semble qu'effectivement le jeu ne peut pas être équitable dans las cas "avec remise", que ce soit à 2 ou à 3 joueurs.
Par contre, dans le cas "sans remise" avec 2 joueurs, je ne trouve pas équiprobabilité dans le cas a=6, b=10. Plus précisément, je trouve une proba de 51/104 que A gagne et une proba de 53/104 que B gagne.
J'ai bien l'impression que le seul cas équitable est a=1, b=2...
Après quelques calculs, il me semble qu'effectivement le jeu ne peut pas être équitable dans las cas "avec remise", que ce soit à 2 ou à 3 joueurs.
Par contre, dans le cas "sans remise" avec 2 joueurs, je ne trouve pas équiprobabilité dans le cas a=6, b=10. Plus précisément, je trouve une proba de 51/104 que A gagne et une proba de 53/104 que B gagne.
J'ai bien l'impression que le seul cas équitable est a=1, b=2...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Après quelques calculs, il me semble qu'effectivement le jeu ne peut pas être équitable dans las cas "avec remise", que ce soit à 2 ou à 3 joueurs.
Par contre, dans le cas "sans remise" avec 2 joueurs, je ne trouve pas équiprobabilité dans le cas a=6, b=10. Plus précisément, je trouve une proba de 51/104 que A gagne et une proba de 53/104 que B gagne.
J'ai bien l'impression que le seul cas équitable est a=1, b=2...
Bonjour Ben314,
Pour le cas a=6 et b=10 je trouve Pa=6/16 = 3/8 et Pb=10/16 x 9/15 = 5/8 x 3/5 = 3/8 et donc Pa = Pb
Ben314 a écrit:Ca me semble plus que louche vu que avec tes valeurs Pa+Pb n'est pas égal à 1 alors que, vu qu'il y a 4 boules B de plus que de A, le match nul est impossible....
Le match nul n'est pas impossible, il a même 2/8 d'être réalisé si d'abord le joueur A tire une boule "B" puis le joueur B tire une boule "A". On a Pnul = 10/16 x 6/15 = 5/8 x 2/5 = 2/8. On a alors Pa + Pb + Pnul = 1 (je ne comprends pas comment tu arrives à 51/104 pour A et 53/104 pour B car de toute façon Pa + Pb ne peut pas faire 1 car il y a toujours des possibilités que la partie soit nulle. C'est comme un match de foot, soit A gagne, soit B gagne, soit c'est match nul)
J'ai effectivement lu l'énoncé de travers : je croyais que les deux joueurs piochaient dans l'urne jusqu'à ce qu'un des deux ait tiré la bonne couleur. Dans ce cas, il ne pourrait pas y avoir de match nul s'il y a franchement plus d'une couleur que de l'autre.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour,
Je fais la démonstration que pour le jeu avec 3 joueurs et remise des boules tirées on ne peut pas trouver 3 nombres a, b et c dans N* pour que le jeu soit équitable. On pose n=a+b+c et on a a a=2A, b=2B, c=2C, n=2N (avec N=A+B+C).
Les équations s'écrivent alors: =
=2B}{(2N)^2}) =
=(2N-2B)2C}{(2N)^3}) soit
soit  =
=B}{N^2}) =
=(N-B)C}{N^3})
C'est une descente infinie puisque A n impair (on note prime les nombres impairs)
Pour la notation, comme a est pair on l'écrit de cette façon , b de cette façon
, b de cette façon  , j'écris n-a qui est impair
, j'écris n-a qui est impair  pour c j'écris
pour c j'écris 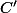 et pour n j'écris
et pour n j'écris 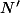
on obtient =
= =
= => impossible. Après réduction les numérateurs des 2 1ère fractions seront pairs alors que celui de la 3ème sera impair
=> impossible. Après réduction les numérateurs des 2 1ère fractions seront pairs alors que celui de la 3ème sera impair
3) a pair, b impair et c pair => n impair. n-b est pair je le note
On obtient =
= =
= c'est impossible après réduction le numérateur de la 1ère fraction est pair celui de la 2ème impair.
c'est impossible après réduction le numérateur de la 1ère fraction est pair celui de la 2ème impair.
4) a pair, b impair et c impair => n pair
On obtient =
= =
= pour les fractions 2 et 3 on a:
pour les fractions 2 et 3 on a:  .
.  =
= .
.  et donc après réduction le nombre de facteur 2 soit au numérateur soit au dénominateur ne pourra pas être le même
et donc après réduction le nombre de facteur 2 soit au numérateur soit au dénominateur ne pourra pas être le même
5) a impair, b pair, c pair => n impair
On obtient =
= =
= => impossible. Le numérateur de la 1ère fraction est impair celui des 2 autres est pair
=> impossible. Le numérateur de la 1ère fraction est impair celui des 2 autres est pair
6) a impair, b pair, c impair => n pair
de Pa=Pb on tire =
= et de Pb=Pc on tire
et de Pb=Pc on tire  =
= et avec
et avec  =
=  on tire
on tire 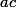 =
= }{2}) cette équation est de la forme
cette équation est de la forme  =
=  soit
soit  =
=  .
. => impossible
=> impossible
7) a impair, b impair c pair => n pair
On obtient =
= =
= soit pour les fractions 1 et 2 on a:
soit pour les fractions 1 et 2 on a: 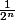 .
. =
= .
. => impossible
=> impossible
8) a impair, b impair, c impair => n impair
 =
= =
= => impossible
=> impossible
Je fais la démonstration que pour le jeu avec 3 joueurs et remise des boules tirées on ne peut pas trouver 3 nombres a, b et c dans N* pour que le jeu soit équitable. On pose n=a+b+c et on a a a=2A, b=2B, c=2C, n=2N (avec N=A+B+C).
Les équations s'écrivent alors:
C'est une descente infinie puisque A n impair (on note prime les nombres impairs)
Pour la notation, comme a est pair on l'écrit de cette façon
on obtient
3) a pair, b impair et c pair => n impair. n-b est pair je le note
On obtient
4) a pair, b impair et c impair => n pair
On obtient
5) a impair, b pair, c pair => n impair
On obtient
6) a impair, b pair, c impair => n pair
de Pa=Pb on tire
7) a impair, b impair c pair => n pair
On obtient
8) a impair, b impair, c impair => n impair
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
