Exo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 01 Déc 2014, 17:32
par adamNIDO » 01 Déc 2014, 17:32
Bonjour,
Français n'est pas ma langue maternelle, donc s'il vous plaît sentir libre de corriger mes réponses et questions.
voici la première partie de l'exo je vais ajouter en fur et en mesure les autres parties
Pour
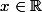
on pose
=x-E(x))
et
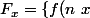;\ n\in\mathbb{N}^*\})
Montrer que :
}\ \forall\ x\in\mathbb{R}: 0\leq f(x)\leq 1.\quad \text{b)}\ \forall\ x\in\mathbb{R}, \forall\ k\in\mathbb{Z}\ :\ f(x+k)=f(x). \quad \text{c)}\ \forall\ x\in\mathbb{R},\ \forall\ p\in\mathbb{N}\ :\ f(p\ x)=f(p\ f(x)))
Poura)
\leq x < E(x)+1 <br />E(x)-E(x)\leq x-E(x)< 1)
pour b]
je sais que
=f(x) \quad \forall x\in\mathbb{R})
est 1-periodique
+k\leq x+k<E(x)+k+1\\<br />E(x)\leq E(x)+k\leq x+k < E(x)+k+1)
Merci pour votre aide
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 01 Déc 2014, 18:46
par zaidoun » 01 Déc 2014, 18:46
Pour a) c'est évident via la propriété suivante E(x) <= x < E(x)+ 1
le b) vient du fait que E(x+k) = E(x) + k pour tout entier k, (c'est facile à le montrer).
le c) On a pour tout p et pour tout x
f (p f(x))= p f(x) - E( p f(x)) = px - pE(x) - E( px - p E(x))= px - pE(x) - E(px) + pE(x) = f(px)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Déc 2014, 19:17
par zygomatique » 01 Déc 2014, 19:17
zaidoun a écrit:Pour a) c'est évident via la propriété suivante E(x) <= x < E(x)+ 1
le b) vient du fait que E(x+k) = E(x) + k pour tout entier k, (c'est facile à le montrer).
le c) On a pour tout p et pour tout x
f (p f(x))= p f(x) - E( p f(x)) = px - pE(x) - E( px - p E(x))= px - pE(x) - E(px) + pE(x) = f(px)
salut
un peu rapide le c) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 01 Déc 2014, 19:38
par zaidoun » 01 Déc 2014, 19:38
juste le passage px - pE(x) - E( px - p E(x))= px - pE(x) - E(px) + pE(x) qui vient de ce que j'ai dit précédemment (E(x + k)= E(x) + k) , ici p E(x) est entier.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 01 Déc 2014, 19:39
par adamNIDO » 01 Déc 2014, 19:39
zaidoun a écrit:Pour a) c'est évident via la propriété suivante E(x) <= x < E(x)+ 1
le b) vient du fait que E(x+k) = E(x) + k pour tout entier k, (c'est facile à le montrer).
le c) On a pour tout p et pour tout x
f (p f(x))= p f(x) - E( p f(x)) = px - pE(x) - E( px - p E(x))= px - pE(x) - E(px) + pE(x) = f(px)
merci beaucoup
conernant
 = E(x) + k pour tout entier k,)
\leq x <E(x)+1\\<br />E(x)+k\leq x+k<E(x)+k+1\\<br />(E(x)+k)\leq (x+k)<(E(x)+k)+1\\<br />comme E(x)+k \in \mathbb{Z} alros E(x+k)=E(x)+k)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 01 Déc 2014, 19:42
par adamNIDO » 01 Déc 2014, 19:42
zygomatique a écrit:salut
un peu rapide le c) ...
merci pour votre attention
-
zaidoun
- Membre Relatif
- Messages: 179
- Enregistré le: 27 Juil 2013, 16:41
-
 par zaidoun » 01 Déc 2014, 19:44
par zaidoun » 01 Déc 2014, 19:44
oui c'est exactement ça :++:
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 01 Déc 2014, 19:48
par adamNIDO » 01 Déc 2014, 19:48
zaidoun a écrit:oui c'est exactement ça :++:
merci beaucoup pour votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
