Question

[biss]

Salut je me demande
La projectile qui n'atteint jamais sa cible est une loi dans l'univers des maths ou juste une erreur de raisonnement ?

[Pseuda]

???? Tu veux parler du paradoxe de Zénon d'Elée, de la flèche qui n'atteint jamais son but, ou d'Achille qui ne rejoint jamais la tortue ?

Il me semble en tout cas que ce n'est pas une erreur de raisonnement : si on arrête le temps, évidemment que la flèche s'arrête. Pendant une durée infinitésimale de temps, la flèche parcourt une distance infinitésimale. Par contre, la somme de ces distances qui deviennent infiniment petites (divisées par 2 à chaque fois), est elle une grandeur finie : la flèche finira par atteindre son but. Je ne vois là aucun paradoxe ni aucune erreur de raisonnement.

Je pense que ce paradoxe vient du fait qu'on peut toujours diviser la distance à parcourir par 2, et donc que la flèche n'atteindra jamais son but. Mais ce faisant, on divise aussi le temps... (si la vitesse est constante).

[biss]

Je parlais de la flèche
Mais en lisant celui de la lièvre et dz la tortue sur wiki, dans la sous chapitrede l'existence de l'infnement petit, il écrivent
On notera aussi qu'à travers ce paradoxe, existe une volonté de montrer que l'infiniment petit n'existe pas. Pensée également partagée par Démocrite, l'inventeur de la notion d'atome. La physique quantique va elle aussi dans ce sens en admettant l'existence d'une unité de temps et d'une unité de taille toutes deux indivisibles — approximativement 10-44 secondes et 10-35 mètres (unités de Planck).
Cela voudrais t-il dire que l'infinement petit n'existe pas en mathématique ??

[Pseuda]

Je parlais de la flèche
Mais en lisant celui de la lièvre et dz la tortue sur wiki, dans la sous chapitrede l'existence de l'infnement petit, il écrivent
On notera aussi qu'à travers ce paradoxe, existe une volonté de montrer que l'infiniment petit n'existe pas. Pensée également partagée par Démocrite, l'inventeur de la notion d'atome. La physique quantique va elle aussi dans ce sens en admettant l'existence d'une unité de temps et d'une unité de taille toutes deux indivisibles — approximativement 10-44 secondes et 10-35 mètres (unités de Planck).
Cela voudrais t-il dire que l'infinement petit n'existe pas en mathématique ??

Démocrite se demandait en effet si on pouvait toujours diviser indéfiniment la matière, ou si à moment donné ce n'était plus possible. Il penchait pour une matière indivisible (les atomes), l'avenir a prouvé qu'il avait raison (à l'échelle de l'atome).

Mais la physique et les mathématiques sont bien différentes. Les mathématiques sont une vue idéalisée de la réalité, et l'infiniment petit existe bel et bien en mathématiques, on le désigne d'ailleurs sous le vocable "dx" (inventé par Leibniz), un infiniment petit de la variable x.

Ce serait comme de dire que des droites parallèles ça n'existe pas (peut-être pas dans la réalité, mais les mathématiques les ont inventées).

[Ben314]

Personnellement j'aurais plutôt tendance à dire que "infiniment petit" n'existe pas en mathématiques (sauf éventuellement en analyse non standard, mais c'est un autre sujet), mais évidement, tout dépend de ce que l'on entend par "infiniment petit".

A mon sens, le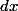 pour un matheux (et pas pour un physicien) il désigne une forme différentielle et ce n'est pas du tout un truc "infiniment petit" (ni même "moyennement petit" d'ailleurs...)
Et, toujours a mon sens, le fait que R est Archimédien ça dit justement qu'il n'existe pas d'infiniment petits dans R.
On peut aussi faire remarquer que les notations de Leibnitz (et de ces contemporains) n'avaient aucune justifications mathématiques rigoureuses : on pourra par exemple consulter la page de wiki https://fr.wikipedia.org/wiki/Histoire_ ... C3%A9simal où ils mentionnent par exemple que "Newton voudrait se débarrasser des quantités infinitésimales qu’il n’arrive pas à baser sur des principes rigoureux" (vers 1670).
Il faut attendre le 19em siècle pour voire apparaitre une définition rigoureuse de la notion de limite (Cauchy et Weierstrass) et donc avoir une définition rigoureuse du "calcul infinitésimal" dans laquelle... disparait toute référence à des "infinitésimaux"...

Sinon, concernant les différent paradoxes formulés par Zénon d'Élée, il me semble (tout à fait discutable...) que le problème réside dans le fait que les matheux grecs refusaient assez catégoriquement tout ce qui pouvait ressembler de près ou de loin à l'infini.
C'est par exemple assez symptomatique, il me semble, dans la "méthode d'exhaustion" qu'il employaient pour calculer des aires/surfaces avec un double raisonnement par l'absurde assez complexe pour éviter de faire ce qu'on appellerais simplement aujourd'hui un "passage à la limite".
Donc je pense qu'il était complètement inconcevable a l'époque de dire qu'une somme infinie de quantités (les temps de parcours successifs de la flèche à chaque étape) puisse donner un résultat fini et je préciserais même qu'a mon avis, ce n'est pas tant le fait que la somme soit fini qui était "inconcevable", mais plutôt le fait qu'une telle somme infinie puisse exister.

Je le redit une fois de plus : ce n'est que ma vision du truc et rien de plus. Mais c'est vrai que ces fameux "paradoxes" grecs sur lesquels se sont penchés de très grand esprit de l'époque semblent assez peu "paradoxaux" a l'heure actuelle et que c'est une question très intéressante de se demander pourquoi.

[biss]

Personnellement j'aurais plutôt tendance à dire que "infiniment petit" n'existe pas en mathématiques (sauf éventuellement en analyse non standard, mais c'est un autre sujet), mais évidement, tout dépend de ce que l'on entend par "infiniment petit".

A mon sens, le pour un matheux (et pas pour un physicien) il désigne une forme différentielle et ce n'est pas du tout un truc "infiniment petit" (ni même "moyennement petit" d'ailleurs...)
Et, toujours a mon sens, le fait que R est Archimédien ça dit justement qu'il n'existe pas d'infiniment petits dans R.
On peut aussi faire remarquer que les notations de Leibnitz (et de ces contemporains) n'avaient aucune justifications mathématiques rigoureuses : on pourra par exemple consulter la page de wiki https://fr.wikipedia.org/wiki/Histoire_ ... C3%A9simal où ils mentionnent par exemple que "Newton voudrait se débarrasser des quantités infinitésimales qu’il n’arrive pas à baser sur des principes rigoureux" (vers 1670).
Il faut attendre le 19em siècle pour voire apparaitre une définition rigoureuse de la notion de limite (Cauchy et Weierstrass) et donc avoir une définition rigoureuse du "calcul infinitésimal" dans laquelle... disparait toute référence à des "infinitésimaux"...

Sinon, concernant les différent paradoxes formulés par Zénon d'Élée, il me semble (tout à fait discutable...) que le problème réside dans le fait que les matheux grecs refusaient assez catégoriquement tout ce qui pouvait ressembler de près ou de loin à l'infini.
C'est par exemple assez symptomatique, il me semble, dans la "méthode d'exhaustion" qu'il employaient pour calculer des aires/surfaces avec un double raisonnement par l'absurde assez complexe pour éviter de faire ce qu'on appellerais simplement aujourd'hui un "passage à la limite".
Donc je pense qu'il était complètement inconcevable a l'époque de dire qu'une somme infinie de quantités (les temps de parcours successifs de la flèche à chaque étape) puisse donner un résultat fini et je préciserais même qu'a mon avis, ce n'est pas tant le fait que la somme soit fini qui était "inconcevable", mais plutôt le fait qu'une telle somme infinie puisse exister.

Je le redit une fois de plus : ce n'est que ma vision du truc et rien de plus. Mais c'est vrai que ces fameux "paradoxes" grecs sur lesquels se sont penchés de très grand esprit de l'époque semblent assez peu "paradoxaux" a l'heure actuelle et que c'est une question très intéressante de se demander pourquoi.

Donc si l'infinezment petit existe, la démonstration de Zénon reste vrai dans l'univers des maths, mais ça changera quoi si c'est vrai ou pas car en math je ne pense pas que les corps se déplace.

[Ben314]

Si tu parle du paradoxe de la flèche où (je cite Wiki) "Si l'instant est trop court, alors la flèche n'a pas le temps de se déplacer et reste au repos pendant cet instant" alors, a mon sens, il y a deux façon de "lever" le paradoxe :

- Soit tu fait de la mécanique "classique", et même en un temps court (voire très court, voire très très court) la flèche se déplace d'une petite distance (voire d'une très petite distance, voire d'une très très petite distance) et l'affirmation cité ci dessus est fausse ce qui lève le paradoxe.
Bien sûr, avec ce point de vue, si tu admet qu'il existe des temps "infinitésimaux", il faut forcément aussi admettre qu'il y ait des distances "infinitésimales" correspondant à ces temps, mais je ne vois pas vraiment de rapport avec le paradoxe en question et absolument rien ne t'oblige à penser que des temps infinitésimaux existent.

- Soit tu fait de la physique quantique et, si j'ai bien compris, le temps avance par à-coups et la flèche se déplace elle aussi par à-coup donc il est plus ou moins vrai qu'en dessous d'une certaine durée de temps, rien ne bouge (sauf qu'a mon avis ça n'a aucun sens de considérer des temps plus petit que le quantum de temps, mais bon...). Mais dans ce cas là, si tu met "bout à bout" de tels temps "trop petit" pour que ça bouge, tu fini par dépasser le temps critique et là, d'un seul coup, ça bouge donc c'est la suite du raisonnement qui ne tient plus la route. De plus, dans ce cas là, je vois encore moins la nécessité d'avoir des temps (ou des longueurs) infinitésimales : on parle de grandeur certes très petites à l'échelle humaine, mais surement pas "infiniment" petites.

[Pseuda]

Personnellement j'aurais plutôt tendance à dire que "infiniment petit" n'existe pas en mathématiques (sauf éventuellement en analyse non standard, mais c'est un autre sujet), mais évidement, tout dépend de ce que l'on entend par "infiniment petit".

A mon sens, le pour un matheux (et pas pour un physicien) il désigne une forme différentielle et ce n'est pas du tout un truc "infiniment petit" (ni même "moyennement petit" d'ailleurs...)
Et, toujours a mon sens, le fait que R est Archimédien ça dit justement qu'il n'existe pas d'infiniment petits dans R.
On peut aussi faire remarquer que les notations de Leibnitz (et de ces contemporains) n'avaient aucune justifications mathématiques rigoureuses : on pourra par exemple consulter la page de wiki https://fr.wikipedia.org/wiki/Histoire_ ... C3%A9simal où ils mentionnent par exemple que "Newton voudrait se débarrasser des quantités infinitésimales qu’il n’arrive pas à baser sur des principes rigoureux" (vers 1670).

Cela me dépasse que l'on puisse dire que l'infiniment petit n'existe pas en mathématiques. Qu'est-ce donc qu'une quantité qui tend vers 0 (comme 1/x quand x tend vers +) d'autre qu'une quantité infiniment petite ? Si on admet que l'infiniment grand existe (qu'est donc + sinon ?), il faut admettre que l'infiniment petit existe aussi ? Et même "0" si ce n'est pas une quantité plus qu'infiniment petite, qu'est-ce que c'est ? Enfin, j'imagine que cela provient de considérations poussées.

Enfin, si on crie sur les toits que l'infiniment petit et grand n'existe pas en mathématiques, je pense que la réaction va être celle-ci : ou bien celle-là :

Par contre, je conçois bien que l'infiniment petit n'existe pas en physique, on est arrêté par la réalité du monde qui nous entoure, et même on doit certainement n'entrevoir qu'une infime partie de cette réalité.

Concernant dx, c'est bien comme une quantité infiniment petite que l'entendaient les mathématiciens qui s'étaient les premiers interrogés sur le calcul différentiel et intégral, et c'est bien comme cela qu'elle est restée dans l'expressionf(x)dx ? Sans le dx (la base des rectangles qui tend vers 0), cela n'aurait pas de sens d'effectuer une somme infinie de quantités finies (à part donner +) ?

[Ben314]

Au dernières nouvelles, une suite qui tend vers 0, c'est une suite qui vérifie :

Et cette définition, je la manipule depuis bien longtemps (trop ?) et pour le moment, j'ai rien vu qui ressemble de près ou de loin à un "infiniment petit" dedans. (donc à un dx au sens de Leibnitz)
Donc question : pour toi, oukilé l'infiniment petit là dedans ? (ou alors tu as une autre définition à proposer ?)

Et si tu me demande (ce qui me surprend un peu) quelle est la valeur de la limite de 1/x lorsque x tend vers +oo (et j'espère que tu es au courant que là dedans, x n'est pas égal à l'infini), alors il me semble bien que c'est très exactement et très précisément égal à 0 et de nouveau, j'aurais pas tendance à dire que c'est un "infiniment petit".

Et concernant +oo toujours aux dernières nouvelles, il me semble bien que ce n'est pas un "nombre" (et que ça n'en sera jamais un). Dans n'importe quel cours un temps soit peu crédible tu lira que des trucs comme 1/oo=0 sont des moyens mnémotechnique pour mémoriser le théorème qui dit que, si une suite Un tend vers +oo (je te recopie pas la définition de "tendre vers l'infini" pour que tu vérifie qu'il n'y a aucune référence à quoi que ce soit d'infiniment petit où grand dedans) alors la suit 1/Un tend vers 0 (mais n'est jamais "infiniment petite).
Ca peut aussi éventuellement aussi être des truc qu'on pose comme définition (mais de nouveau, le 1/+oo il est parfaitement totalement égal à 0 et pas à un "infiniment petit")

Et concernant le passage concernant le on crie sur les toi... je pense... tout pareil sauf le début de la phrase.

Sur la fin de ta prose, on est parfaitement d'accord : au 18em siècle, on faisait des calculs avec des infinitésimaux (au grand damn de beaucoup de matheux dont Newton le premier qui voyait bien que ce n'était pas rigoureux). Depuis, on a heureusement fait des progrès...
En bref, pour moi, affirmer que les infinitésimaux existent an math, ça veut dire en être resté au 18em siècle...

[biss]

Pour 1/x, si on fait tendre x vers des valeurs infinement grand alors il est normale que 1/x tend vers un nombre infinement petit.
J'ai du mal à comprendre comment 1/x=0 pour une valeur de x précis.

[Ben314]

Pour 1/x, si on fait tendre x vers des valeurs infinement grand alors il est normale que 1/x tend vers un nombre infinement petit.
J'ai du mal à comprendre comment 1/x=0 pour une valeur de x précis.

On ne fait pas "tendre x vers des valeur infiniment grandes", on fait "tendre x vers l'infini" et, de même, ce n'est pas "1/x qui tend vers un nombre infiniment petit" mais "1/x qui tend vers zéro"

Sinon, concernant 1/x, il y a deux possibilités :
- Soit tu prend un x donné (éventuellement très grand) et 1/x n'est pas du tout nul, mais il n'est pas non plus infiniment petit.
- Soit tu prend la limite de la fonction 1/x quand x tend vers l'infini et là il y a une définition extrêmement rigoureuse (avec des epsilon) qui te dit que cette limite est très exactement égale à 0 donc pas plus d'infiniment petit que de beurre en branche dans ce cas là non plus.
Tu voit un troisième cas toi ? Moi j'en vois pas.

Sinon, je viens de tomber là dessus :
Ces notions qui reposent sur des ”infiniment petits” que personne n’a jamais pu définir, ont fait inutilement cogiter et divaguer beaucoup trop de gens pour qu’on leur attribue maintenant un autre rôle que celui d’une explication historique de la notation différentielle.
R.Godement, 1998, Analyse mathématique, Volume I, [p.260]
Ca ne prouve évidement rien, mais ça montre au moins que je suis pas le seul a penser que les infinitésimaux n'ont plus rien a voir avec les mathématiques actuelles (et si tu y tient, je pense pouvoir à l'aise te donner une bonne douzaine de citations allant exactement dans le même sens)

[Sylviel]

les infinitésimaux n'ont plus rien a voir avec les mathématiques actuelles

Juste pour faire râler : https://fr.wikipedia.org/wiki/Analyse_non_standard

Ceci étant dit, en analyse standard, 1/x tends bien vers 0 quand x tends vers l'infini. 1/x n'est donc jamais "infiniment petit".

[Sake]

@Ben : Dans la définition de la limite formalisée par Cauchy et cie, on peut lire "pour un epsilon quelconque", ce qui peut aussi dire "pour un epsilon aussi petit que l'on veut". Si sur ce point-là, tu n'as rien à redire, alors pourquoi ne peut-on pas associer ce terme à "pour un epsilon infiniment petit" ?

Si tu as des choses à redire sur "pour un epsilon aussi petit que l'on veut" (sur sa valeur sémantique ainsi que sur son côté arbitraire), pourquoi ? Selon moi, cette formulation a certainement quelques défauts mais ils me semblent insignifiants : par exemple, on élimine certains cas de figure (dont les epsilon aussi grands qu'on veut ou des epsilon tout à fait quelconques), mais ce n'est important à la mesure de ce qu'on démontre par l'emploi de cet outil, qui représente au final une sorte de curseur.

Edit : je viens de te relire et ce qui te pose un pb c'est la notion d'infiniment petit. Au final tout epsilon que l'on prend a une valeur finie. Quand on fixe un réel donné, il existe une précision finie et en ce sens je te comprends tout à fait. Mais la définition de Cauchy ne signifie-t-elle pas que l'on puisse faire varier cet epsilon et le diminuer toujours plus en le faisant tendre vers 0 (et, ce faisant, en changeant la précision êta, etc.) ?

[Ben314]

les infinitésimaux n'ont plus rien a voir avec les mathématiques actuelles

Juste pour faire râler : https://fr.wikipedia.org/wiki/Analyse_non_standard

ca ne me fait absolument pas râler vu que mon premier post. commençait justement par

..."infiniment petit" n'existe pas en mathématiques (sauf éventuellement en analyse non standard...)

De plus, pour en avoir pas mal fait à une époque, je sais qu'avant de pouvoir parler d'entiers "illimités" (on utilise plutôt cette expression là que celle "d'infiniment grand") il faut avoir précisé ce que l'on entendait par "entier standards" (un illimité est un entier plus grand que tout les entiers standards) et que là, pour appréhender correctement la notion, c'est pas gagné...

[Ben314]

Concernant la définition de Cauchy, tu peut parfaitement si ça t'arrange, voir intuitivement cet epsilon comme un infiniment petit, mais stricto senso, la définition dit uniquement "pour tour epsilon>0".
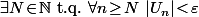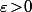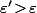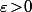Aprés, quand on enseigne cette définition, c'est effectivement on ne peut plus utile de faire constater que, si on note la proposition "" alors le fait que soit vraie pour un certain implique trivialement que est aussi vraie pour tout et cela signifie que, pour montrer que est vraie pour tout il suffit en fait de montrer que c'est vrai pour les "petits" , c'est à dire que, si nécessaire lors d'une preuve, ça ne coute rien de supposer par exemple .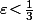

Et si je "refuse" les infinitésimaux, c'est parce que l'infini, sous à peu prés toute ces formes, je m'en méfie profondément : y'a qu'à voir le nombre impressionnant de "paradoxes" voire de véritables "contradiction" liés à l'infini qui on émaillées l'histoire des mathématiques pour voir que ce n'est pas un truc qu'on manipule à la légère.
Et là, concernant l'analyse, depuis Cauchy et Weierstrass, on arrive à tout modéliser (=définir) sans aucune référence à quoi que ce soit d'infini : on ne fait plus que des "passages à la limite" dont la définition ne fait aucunement référence à l'infini. Et à mon sens, c'est bien mieux ainsi (par exemple, je pense pas que ce soit malin pédagogiquement parlant d'introduire l'analyse non standard "tôt" pour faire de l'analyse)

Mais la définition de Cauchy ne signifie-t-elle pas que l'on puisse faire varier cet epsilon et le diminuer toujours plus en le faisant tendre vers 0 (et, ce faisant, en changeant la précision êta, etc.) ?

Si tu commence à dire que, dans la définition en question tu "fait tendre epsilon vers 0", ça se mord complètement la queue vu que justement, ce que tu est en train de définir, c'est le sens de l'expression "tendre vers" (ou alors tu as préalablement une autre définition de "tendre vers" et à ce moment là, celle de Cauchy te sert plus à rien vu que tu en a déjà une...)

Et sinon, je le redit une deuxième fois (de façon plus explicite), mais l'axiome d'Archimède (qu'on démontre si on construit R et qu'on admet si on part d'une définition axiomatique de R), il dit que :
Quelque soient les réels x et y strictement positif, il existe une somme finie x+x+x+...+x qui est strictement plus grande que y.
Et pour moi, le mot fini qui apparait là dedans, il dit très exactement qu'il n'existe pas de x infiniment petit ni de y infiniment grand.

[Robot]

Les infinitésimaux sont pourtant utilisés dans un domaine où il pourrait sembler a priori qu'ils n'ont pas leur place : l'algorithmique. On pourra par exemple en trouver dans le livre "Algorithms in Real Algebraic Geometry". Typiquement, ils sont utilisés pour perturber une situation singulière afin de se ramener à une situation non-singulière générique. Pour ce faire, on étend le corps des réels par un infinitésimal, en gardant toutes les propriétés algébriques des réels, et en ayant un bon contrôle sur les objets introduits.
Techniquement, on considère une extension ordonnée non archimédienne où est positif et plus petit que tous les réels positifs, et on travaille avec la clôture réelle de ce corps ordonné, qui est le corps des séries de Puiseux algébriques en à coefficients réels.

[Pseuda]

@Ben314
Je peux t'assurer que tous ceux à qui j'en ai parlé aujourd'hui ont ouvert des yeux grands d'étonnement à l'affirmation que l'infiniment petit n'existait pas en mathématiques, voire n'étaient franchement pas d'accord.

Il me semble que la confusion vient du fait que :

Pour moi, comme pour le commun des mortels :

"l'infiniment petit existe" = "on peut toujours trouver un nombre plus petit qu'un nombre donné"
"l'infiniment grand existe" = "on peut toujours trouver un nombre plus grand qu'un nombre donné"
"l'infiniment grand n'existe pas" = "il existe un nombre plus grand que tous les autres nombres"
"l'infiniment loin existe" = "on peut toujours aller plus loin qu'un point donné"
etc...

Pour toi :

"l'infiniment petit n'existe pas en mathématiques" = "le concept sur lequel s'appuyaient les mathématiciens qui ont fondé l'analyse mathématique est dépassé, source d'erreurs, etc... ; ce concept n'existe plus dans l'analyse d'aujourd'hui, etc...".

Enfin, ce n'est pas parce qu'on ne parle pas d'une chose que cette chose n'existe pas. Toute l'analyse mathématique est quand même fondée sur le concept de l'infiniment petit et grand tel qu'il est compris par le commun des mortels. Et même si dans l'analyse d'aujourd'hui on n'en parle pas, il doit bien se trouver niché quelque part et accepté implicitement ?

[Robot]

Pour moi, comme pour le commun des mortels :
"l'infiniment grand existe" = "on peut toujours trouver un nombre plus grand qu'un nombre donné"

"L'infiniment grand existe" (ou disons plus clairement : "Il existe un nombre infiniment grand") veut dire qu'il existe un nombre plus grand que tous les entiers naturels standards.

[Ben314]

Si tu considère que, sur une question de ce type, la "bonne réponse" on la trouvera en interrogeant le "commun des mortels" plutôt que dans un livre (d'enseignement ET d'analyse) de Roger Godement, alors, effectivement, il est tout a fait normal qu'on arrive pas aux mêmes conclusions.

[biss]

@Ben314
Je peux t'assurer que tous ceux à qui j'en ai parlé aujourd'hui ont ouvert des yeux grands d'étonnement à l'affirmation que l'infiniment petit n'existait pas en mathématiques, voire n'étaient franchement pas d'accord

Comme moi, je me suis basé plein de fois sur ces deux notion pouir faire mes raisonnement. Mais qui le monde an décide autrement alors je n'ai pas le choix que de l'accepter même si jusqu'à présent je me demande comment ces possibles voir même comment peut dire qu'il existe un nombre plus grand que tous les autres.