PSEUDA a écrit:Par ailleurs, tout ceci ne m'empêchera pas de continuer à répondre à mes élèves (qui ne sont pas au courant des batailles du 18ème siècle) et qui demandent ce qu'est le "dx" du

f(x)dx, plutôt que de répondre "c'est une notation" (réponse très frustrante et qui à mon avis embrouille), de répondre que c'est une quantité infiniment petite (qui autorise à faire la somme de quantités finies)
et qui indique la variable d'intégration. Sinon, quelle autre explication donner à "dx" ?
Au Lycée, je ne sais pas ce que je répondrais, mais à la fac, très clairement, je donne exclusivement ta deuxième réponse (soulignée) et je ne me gène pas (*) pour utiliser la notation

sans

ni
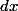
lorsque

est une fonction d'une seule variable, ni même celle de
)
(a un niveau un peu plus élevé) pour une fonction de deux variables.
Par contre, évidement, dans le cas d'une intégrale double
écrite avec les notation de Riemann, il faut forcément mettre les
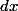
et
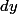
pour savoir quelles sont les bornes qui correspondent aux x et quelles sont celles qui correspondent aux y.
Mais si tu l'écrit "à la Lebesgue" en mettant une partie de
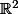
en indice, tu peut de nouveau ne mettre ni
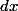
, ni
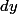
(et je ne me gène pas pour le faire...)
(*) Et je ne pense pas être une "exception"...
PSEUDA a écrit:De dire à des élèves de Terminale que l'infiniment petit et grand n'existe pas en mathématiques ne peut, à mon avis, que les embrouiller.
Et c'est là qu'on est clairement pas d'accord vu que je suis persuadé que
ça ne peut que les embrouiller et je rajouterais que, si je voyais un de mes anciens étudiants capésien revenir me voir en me disant qu'il parle à ces élèves "d'infiniment grand" et "d'infiniment petits", je pense que je m'autoriserais à "lui passer un savon" de première.
PSEUDA a écrit:En fait, elle caractérise que l'ensemble n'a pas de plus grand élément. Mais ce qui différencie ces 2 ensembles (]3,4[ et R) inclus dans R, c'est que l'un est majoré dans R, l'autre ne l'est pas (sauf par +oo, encore l'infini...)
Bilan : si tu veut un majorant de ]3,4[, il faut le cherche
en dehors de ]3,4[ et si tu veut un majorant de R, il faut le chercher
en dehors de R => jusque là, c'est très exactement la même chose.
PSEUDA a écrit:Mais je ne vois toujours pas là en quoi il faut bannir l'infiniment petit et grand du langage mathématique. Mais c'est pas grave.
J'ai la flemme de faire le boulot à ta place, mais je te suggère de regarder la (très nombreuse) littérature écrite par les (très nombreux) détracteur de Newton, Leibnitz et leurs successeurs (avant Cauchy et Weierstrass bien sûr) qui expliquent qu'en utilisant des infiniment petits on tombe rapidement sur des paradoxes (au mieux) voir des trucs réellement contradictoires.


