Intégrabilité

[valsad]

Bonjour,

Comment montrer que la fontion e^(-t)ln(t) est intégrable sur ]0,+;)[?
Je pense qu'il faut montrer qu'elle est localement intégrable sur [1,+;)[ et sur ]0,1] mais je n'arrive pas à trouver de fonctions équivalentes ou de majoration dont l'intégrale converge!

Quelqu'un a une idée?

Merci.

[mathelot]

Bonjour

est bornée sur

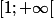
disons que l'on garde un peu d'exponentielle pour la convergence
et un peu pour se débarasser du log :we:

au voisinage de zéro, l'intégrande

i) garde un signe constant
ii) équivaut à ln(t) , localement intégrable, de primitive

[valsad]

Merci pour ta réponse mais sur [1,+;)[ je ne vois pas par quoi on peut borner e(-t)ln(t)!

Tu peux m'éclairer stp?

Merci.

[girdav]

Par exemple on a et on peut montrer facilement que l'intégrale est convergente (par exemple en intégrant par parties de à ).

[valsad]

ok! Je n'avais pas du tout pensé à majorer par t*e^(-t)!

Merci beaucoup!