Critere d'integrabilite de Riemann

[MathematicienPoche]

Bonsoir,

j'essaye de resoudre ce probleme:

f(x) = 2 si x negale pas 1/2, 0 si x egal 1/2.

Montrer que f est integrable sur [0,2].

J'ai essayer une piste... j'ai trouver que S(f,p) = 4 et s(f,p) = 4(n-1)/n si on prendre une partition avec interval 1/n, alors lorsqu'on fait tendre n dans S(f,p) - s(f,p) vers linfini on obtient 0, et donc que lintegrale inferieur est egale a lintegrale superieur. Est-ce bon?

Si oui, ya til un moyen de passer directement par le critere, cest-a-dire par S(f,p) - s(f,p) < E. Je ne saisis pas vraiment comment resoudre ce type de probleme... merci a ceux qui pourront m'aider!

[Nightmare]

Salut :happy3:

Il faut revenir à la définition de l'intégrale de Riemann.

On se fixe une subdivision ordonnée .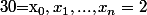

On se donne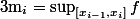 et .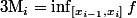

f va être intégrable au sens de Riemann sur [0,2] si et ssi les sommes inférieures et supérieures : et ont la même limite.

A toi de terminer. Pour t'aider, essayer de voir les valeurs que peuvent prendre les mi et les Mi.

:happy3:

[ffpower]

si on dit que f est continue par morceaux,ca suffit pas?

[Nightmare]

A priori le but de l'exercice est justement de manier la définition, d'où mon message.

[ffpower]

ok,c est possible..(a vrai dire dans ma prepa,c était "integrable <=> continue par morceaux lol)

[MathematicienPoche]

D'accord... mais dans ce cas mi = 2, seulement pour les intervalles de la somme ne contenant pas 1/2. Donc, comment est-ce que je peux definir s(f,p)? Merci.

[SimonB]

Combien y a-t-il au maximum d'intervalles de la somme contenant 1/2 ?

[quinto]

ok,c est possible..(a vrai dire dans ma prepa,c était "integrable continue par morceaux lol)

Pourtant c'est faux.

[ffpower]

ouai ouai je sais.cela dit on disait pas "integrable au sens de riemann",donc qui sait?c était p-e "intégrable au sens de mon prof de prepa" mdr

[Nightmare]

Ah bon ffpower? C'est quand même bizarre parce que le programme de sup sur l'intégrale de Riemann est justement fait pour détailler sa construction ! Ton prof a dû omettre de son gré cette partie, assez lourde pour les élèves :lol3:

[quinto]

Bizarre mais pourquoi pas, je trouvais ça bien lourd moi aussi quand je le faisais...

[mathelot]

euh,
en dimension 1, il me semble que f Riemann-intégrable équivaut
à "f à variations bornées" , c'est à dire différence
de deux fonctions croissantes.

sauf erreur.

[quinto]

Tu es sur ?
Il me semble qu'une fonction définie sur un compact est Riemann intégrable ssi l'ensemble de ses points de discontinuité est de mesure nulle.

La fonction caractéristique d'un Cantor de mesure nulle, disons K3, est donc Riemann intégrable, n'est-ce pas ?

Il me semble aussi qu'une fonction croissante est discontinue en un nombre au plus dénombrable de points, donc il en est de même d'une différence de telles fonctions, est-ce que je me trompe ?

[ffpower]

Ah bon ffpower? C'est quand même bizarre parce que le programme de sup sur l'intégrale de Riemann est justement fait pour détailler sa construction ! Ton prof a dû omettre de son gré cette partie, assez lourde pour les élèves :lol3:

J étais en psi,ceci explique p-e cela^^
Une question:est ce que une limite simple de fonctions continues est riemann integrable?car pour moi,du coup,ca c était lourd,fallait a chaque fois vérifier la continuité de la limite pour faire une convergence dominée..

[SimonB]

En sup MPSI, le programme, c'est : intégrale de Riemann d'une fonction c.p.m. sur un segment.

En spé MP : intégrale sur des segments quelconques de fonctions encore c.p.m.

[Nightmare]

Oui !

Ceci est vrai car une limite simple de fonction continue est continue presque partout au sens de Baire, donc intégrable. (Sur un compact, toujours)

[Nightmare]

Par contre, si on considère juste une limite simple de fonctions Riemann-intégrable, elle n'est pas forcément Riemann-intégrable.

Par contre dans la théorie de Lebesgue, si l'on rajoute une hypothèse de monotonie, une limite simple de fonctions intégrables au sens de Lebesgue monotone est intégrable en ce sens. (théorème de convergence monotone)

[ffpower]

Oui !

Ceci est vrai car une limite simple de fonction continue est continue presque partout au sens de Baire, donc intégrable. (Sur un compact, toujours)

Ah..dans ce cas c est quand meme pratique d avoir vu la def générale alors en effet...sinon qu est ce que tu entends par "presque partout au sens de baire"?que ca contient un Gdelta dense?

[quinto]

Par contre, si on considère juste une limite simple de fonctions Riemann-intégrable, elle n'est pas forcément Riemann-intégrable.

Par contre dans la théorie de Lebesgue, si l'on rajoute une hypothèse de monotonie, une limite simple de fonctions intégrables au sens de Lebesgue monotone est intégrable en ce sens. (théorème de convergence monotone)

Il faut aussi une hypothèse supplémentaire en général, comme par exemple une hypothèse de positivité ou de minoration si la mesure de l'espace est finie.

[ffpower]

Par contre, si on considère juste une limite simple de fonctions Riemann-intégrable, elle n'est pas forcément Riemann-intégrable.

Par contre dans la théorie de Lebesgue, si l'on rajoute une hypothèse de monotonie, une limite simple de fonctions intégrables au sens de Lebesgue monotone est intégrable en ce sens. (théorème de convergence monotone)

d ailleurs,un petit exo la dessus,c est de montrer que si un ensemble contient les fonctions continues et est stable par limite simple,alors il contient toutes les fonctions mesurables..(par mesurable,j entend borelienne).En particulier,c est donc sur qu une limite de fonctions riemann integrables n est pas forcément riemann integrable^^