Circuits dans un billard

[leon1789]

(...)Cela prouve que la trajectoire boule de billard est le trajet le plus long.

Je n'ai pas compris quelle était ton hypothèse, mais une trajectoire boule de billard n'est pas toujours le trajet le plus long : dans un carré (avec coins arrondis...), il y a plein de trajectoires à 4 points, et ils ne sont pas tous de la même longueur.

[Imod]

Petit correctif à ma figure avant de lire la suite : tout point au dessus de donne .


Imod

[leon1789]

Petit correctif à ma figure avant de lire la suite : tout point au dessus de donne .
Imod

oui uniquement quand D est la tangente au point B de l'ellipse ayant pour foyers A et C.

[Imod]

N'est-ce pas ce qu'indique mon dessin ?

Imod

[nodjim]

Je n'ai pas compris quelle était ton hypothèse, mais une trajectoire boule de billard n'est pas toujours le trajet le plus long : dans un carré (avec coins arrondis...), il y a plein de trajectoires à 4 points, et ils ne sont pas tous de la même longueur.

Avec, bien entendu, un point fixe donné au départ. Il y a une trajectoire maximale pour un point fixe donné et N-1 autres points, c'est ça le Ngone.

[leon1789]

Donc, on devrait pouvoir dire: le Ngone inscrit dans un convexe a forcément une longueur maximale. donc c'est la trajectoire d'une boule de billard. Donc ça prouve son existence.

Avec, bien entendu, un point fixe donné au départ. Il y a une trajectoire maximale pour un point fixe donné et N-1 autres points, c'est ça le Ngone.

Ok, le point A est fixé dans ton Ngone de périmètre maximal.
Je ne suis pas convaincu qu'en A, les angles d'incidence et de réflexion soient égaux.

[leon1789]

Imod,
ton dernier dessin

avec ta preuve adaptée
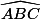
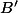
\ \widehat{NBC}[/TEX] et le bord traverse en la bissectrice extérieure D de l'angle . En prenant un point du bord au-dessus de D, on obtient qui est en contradiction avec l'hypothèse . montre que ABC...YZ n'est pas de périmètre maximal.
>>
justifient essentiellement la contraposée : es-tu d'accord ?
Tu vas me dire que tu ne vois pas de différence entre une contraposée et une preuve par l'absurde (utilisant toutes les deux le tiers exclu).

Voilà comment je vois les choses.
Le dessin est ici un dessin qui "colle" avec ta démo de la contraposée : ABC n'est pas un trajet de bille et on voit qu'on peut augmenter la distance AB+BC en AB'+B'C.
(Plus haut, le dessin que j'ai présenté "colle" avec ma démo directe : AB+BC est maximal et on voit que ABC est un trajet de bille.)
A contrario, un dessin ne pourra jamais "coller" avec une preuve par l'absurde puisqu'il faudrait réussir à réaliser l'impossible... Donc une preuve par l'absurde se fera toujours sur un croquis faux (ce qui n'empêche pas de faire des raisonnements corrects, cf adage que tu rappelais :we: )

Pour moi, cette différence d'illustration qui colle au texte est importante (pédagogiquement parlant). Qu'en penses-tu ? Qu'en pensez-vous ?

[nodjim]

Ok, le point A est fixé dans ton Ngone de périmètre maximal.
Je ne suis pas convaincu qu'en A, les angles d'incidence et de réflexion soient égaux.

Je comprends; on peut toujours fixer A au départ, et l'ajuster en cours de construction. On ne sait pas exactement quel sera son emplacement au final, je suis d'accord. Cela étant dit, il y a peut être une seule solution, ou peut être plusieurs, selon le A fixé au départ.

[ramon717]

il manque des element pour que ta conjecture soit vrai
parceque la je te montre un contre exemple en tapant tout doucement la bille qui n'ira toucher aucune bande , merci la force de frottement

ok je sort :zen:

[mathieuH]

Bonjour,

je suis tombé sur une démo un peu plus courte:
http://www.les-mathematiques.net/c/a/b/node21.php3#bbillard

bon billard.