Circuits dans un billard

par **Imod** » 06 Juil 2009, 07:36

Bonjour

On considère un billard plan convexe dont le bord nest pas anguleux ( de classe C1 ) . Montrer que pour tout entier

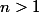
il existe une trajectoire périodique à n rebonds dans le billard ?

Amusez-vous bien :zen:

Rappel : une boule de billard rebondit comme un rayon lumineux : angle réfléchi = angle d'incidence .

Imod

par **Maks** » 06 Juil 2009, 10:30

Oral d'ENS ...

par **nodjim** » 06 Juil 2009, 16:04

Imod a écrit:

...dont le bord nest pas anguleux ( de classe C1 ) .
Imod

Peux tu préciser ?
Sinon, il me semble que ça se résoud par symétrie ce truc.

par **Imod** » 06 Juil 2009, 16:12

nodjim a écrit:Peux tu préciser ?

Le bord est continu et admet une tangente ( unique ) en chaque point . Le billard peut très bien ne pas admettre d'élément de symétrie .

Imod

par **Maks** » 06 Juil 2009, 16:21

C'est pas la définition de dérivable ça ?

par **nodjim** » 06 Juil 2009, 16:28

Imod a écrit:Le bord est continu et admet une tangente ( unique ) en chaque point . Le billard peut très bien ne pas admettre d'élément de symétrie .

Imod

Je connais la solution. Elle tient juste dans une représentation mentale. Elle fait appel à la symétrie pour la construction.

par **Maks** » 06 Juil 2009, 16:29

Peux-tu préciser s'il te plaît ?

par **Imod** » 06 Juil 2009, 17:45

Maks a écrit:C'est pas la définition de dérivable ça ?

Oui , en fait dérivable devrait suffire , par contre j'avais oublié convexe que j'ai rajouté dans le message initial .

Imod

par **Maks** » 07 Juil 2009, 09:15

J'ai l'exercice corrigé dans un bouquin mais ils utilisent un bord

.

par **Imod** » 07 Juil 2009, 10:19

Il est clair que la condition

est trop forte , l'idée étant que si

et

sont deux points du billard et

un point du bord alors

dépend continument de

.

Imod

par **jamys123** » 07 Juil 2009, 14:14

j'ai joué au billard toute l'après-midi, mais je suis plus en état pour répondre...

par **nodjim** » 07 Juil 2009, 18:25

J'ajoute que non seulement on peut choisir le nombre de rebonds dans la période, mais en plus, on peut définir le nombre de rebonds sur le grand coté et celui sur le petit coté.

par **Maks** » 07 Juil 2009, 18:45

Le billard n'a a priori rien de rectangulaire ! Pas question de parler de côtés !

par **Imod** » 07 Juil 2009, 23:39

Oui le billard peut très bien avoir une forme d'ovale , d'ellipse , d'oeuf , ... , tant qu'il reste suffisamment lisse et convexe .

Imod

par **nodjim** » 08 Juil 2009, 15:35

D'accord, je n'avais pas compris cela. Je ne connais pas alors. :triste:

par **nodjim** » 09 Juil 2009, 16:38

Soient A, B, C, D,...des points sur la circonférence du plan.
A est fixe et une trajectoire vise B puis par rebond atteint C et enfin D.
Si B est proche de A et s'en éloigne, C va aussi fuir, et D également. C va environ 2 fois plus vite que B, et D 3 fois plus vite que B. (valeurs justes sur un cercle parfait, et juste en moyenne pour un tour complet de B). Quand D rejoint A, on a fait un rebouclage en triangle.
Même raisonnement quelque soit le nombre de points.

Il est à noter qu'il existe un point sur le convexe, et un seul, tel que la perpendiculaire à la tangente passe par A. Lorsque B est à cet endroit tous les points suivants sont confondus soit avec A, soit avec B.

par **skilveg** » 09 Juil 2009, 16:56

C'est intuitivement bon mais pas très formel! (D'un autre côté je crains que formaliser cette idée ne soit un brin compliqué)

Question: quelqu'un connait un billard

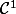
non convexe pour lequel il existe des entiers pour lesquels il n'y a pas de trajectoire périodique?

par **Imod** » 09 Juil 2009, 22:41

nodjim a écrit:Soient A, B, C, D,...des points sur la circonférence du plan.
A est fixe et une trajectoire vise B puis par rebond atteint C et enfin D.

Pourquoi ne pas choisir A , B , C et D au hasard et se souvenir que la nature choisit toujours les trajets à moindre effort :zen:

Imod

par **nodjim** » 10 Juil 2009, 04:33

Imod a écrit:Pourquoi ne pas choisir A , B , C et D au hasard et se souvenir que la nature choisit toujours les trajets à moindre effort :zen:

Imod

Comprends pas.

par **Imod** » 10 Juil 2009, 10:11

nodjim a écrit:Comprends pas.

Je ne voulais pas être trop explicite :we:

Considère l'ensemble des quadruplets (A,B,C,D) sur le bord ( ne t'occupe pas de savoir si c'est une trajectoire de billard ou pas ) puis observe AB+BC+CD+DA qui dépend continûment du quadruplet choisit et atteint donc ses bornes ...

Je te laisse finir :zen:

Imod

Circuits dans un billard

Circuits dans un billard

Qui est en ligne