Equation quadratique
Olympiades mathématiques, énigmes et défis
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Aoû 2008, 12:35
par lapras » 17 Aoû 2008, 12:35
Bonjour,
Trouver tous les triangles recatngles à cotés entiers et dont l'aire est un carré parfait.
Bonne chance
Lapras :we:
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 12:46
par miikou » 17 Aoû 2008, 12:46
salut, lapras.
Je crois qu'il n'en existe pas, ai-je raison ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Aoû 2008, 13:11
par lapras » 17 Aoû 2008, 13:11
oui !
Preuve ? :we:
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 13:28
par miikou » 17 Aoû 2008, 13:28
mdr jai supprimé le message, je disais non il n'en existe pas.
pour la preuve je considere un triplet pythagoricie
a= k(u²-v²) b= 2kuv avec pgcd(u,v)= 1
on aurait donc a*b/2 = z²
soit encore k²*(uv)*(u²-v²)= z² => uv*(u²-v²)= y² il est facile de constater que u et v sont inferieurs y donc
u| y² => u | y => y u*n
v|y² => v| y => y= v*m
donc u*n= v*m or pgcd (u,v) = 1 donc v | n => n= p*v
finalement y = u*n = p* vu
en ré injectant dans lequation de dépard on arrive à : (u²-v²)= p²*u*v
donc u divise u²-v² donc u divise v² absurde
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Aoû 2008, 13:45
par lapras » 17 Aoû 2008, 13:45
u | y² n'implique pas que y = k*u
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 13:49
par miikou » 17 Aoû 2008, 13:49
u divise y ..
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 13:57
par magnolia86 » 17 Aoû 2008, 13:57
en plus de la remarque de Lapras (

n'implique pas

...

n'est pas premier, par exemple), j'ajoute
miikou a écrit:a= k(u²-v²) b= 2kuv avec pgcd(u,v)= 1
(...) donc u divise v² absurde
ce n'est pas absurde : ça donne

-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Aoû 2008, 13:58
par lapras » 17 Aoû 2008, 13:58
non
u divise y²
par exemple
2^4 divise (3*2^2)^2 mais ne divise pas (3*2^2)
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 14:08
par miikou » 17 Aoû 2008, 14:08
magnolia86 a écrit:en plus de la remarque de Lapras (

n'implique pas

...

n'est pas premier, par exemple), j'ajoute
ce n'est pas absurde : ça donne

mdr ? on parle de longueur d'un triangle or 1+1 = 2 qui n'est pas un carré parfait.
De plus tu semble ne pas avoir compris pk u|y² => u|y², je l'avais passé sous silence pensant que c'etait evident ..
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 14:12
par magnolia86 » 17 Aoû 2008, 14:12
miikou a écrit:mdr ? on parle de longueur d'un triangle or 1+1 = 2 qui n'est pas un carré parfait.
c'est a, b les longueurs, et pas u,v !
Edit : ok, pour moi, il manque un petit choua d'explication, bon passons...
miikou a écrit:De plus tu semble ne pas avoir compris pk u|y² => u|y, je l'avais passé sous silence pensant que c'etait evident ..
non, j'ai pas compris, et je ne suis pas le seul a priori.
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 14:42
par miikou » 17 Aoû 2008, 14:42
désolé si des fois je suis un peu rapide quant a l'explication :doh:
bon commençons par le plus simple prend les couples u,v
u=v = 1 => un des cotés est réduit a 0, u = v = -1 a= 0,b = 2*k, idem.
maintenant par symétries des rôles on suppose que u=1 et v=-1
a= 2k b=-2K or a,b>0 absurde
u|k²
v|k²
k² est un multiple du ppcm( u,v), comme pgcd(u,v) = 1 ppcm(u,v) = u*v
donc k² = S*uv ( avec S supérieur a 1)
on revient a notre équation
(u²-v²)*uv = k² <=> (u²-v²)*uv= S*uv
si S=1 u²=v² on a u= +/- 1 v = +/- 1 alors on conclut d'après ce que j'ai écrit précédemment.
Il reste le cas S > 1
u²-v²= (S-1)uv
donc u divise v² ce qui nous rament aussi a la remarque du début : conclus :++:
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 15:21
par magnolia86 » 17 Aoû 2008, 15:21
miikou a écrit:on revient a notre équation
(u²-v²)*uv = k² (u²-v²)*uv= S*uv
si S=1 u²=v² on a u= +/- 1 v = +/- 1 alors on conclut d'après ce que j'ai écrit précédemment.
Il reste le cas S > 1
u²-v²= (S-1)uv
donc u divise v² ce qui nous rament aussi a la remarque du début : conclus :++:
Si S=1 ? ou S=0 ? Et comment arrives-tu à u²-v²= (S-1)uv ?
Pour moi, (u²-v²)*uv= S*uv ( S=u²-v² ou u=0 ou v=0 )
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 15:34
par magnolia86 » 17 Aoû 2008, 15:34
Je donne ma solution (malheureusement plus compliquée que je pensais au début...) quant à la résolution du système

avec

.
Comme l'a rappelé miikou,
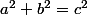
implique que l'on peut écrire
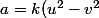)
et

avec
=1)
.
Or

donc
uv = (d/k)^2)
.
Mais un nombre rationnel dont le carré est entier, est lui-même entier. Donc
uv = e^2)
avec

.
Maintenant, on utilise le fait que

et

sont premiers entre eux, ce qui implique qu'ils sont aussi premiers avec
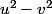
.
Du coup, cela force

a être des carrés tous les trois ! Posons

, si bien que

Or cette équation n'a pas de solution autre que celles évidentes (là, ça demande des détails (*)) : y=0 ou z=0. Ainsi v=0 ou

, ce qui implique respectivement
b=0 ou a=0.
(*)
http://planetmath.org/encyclopedia/X4Y4z2HasNoSolutionsInPositiveIntegers.html
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 15:41
par miikou » 17 Aoû 2008, 15:41
j'ai ecris nimporte quoi en effet :ptdr:
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 17 Aoû 2008, 16:38
par nodgim » 17 Aoû 2008, 16:38
Je donne, avec la même conclusion, une autre approche:
Si N pair, les solutions qui satisfont a²+b²=c² sont de la forme, pour b si a est N: (N²/4i)-i avec N²/4i entier pair.
Et N/2*((N²/4i)-i) n'est pas un carré.
Si N impair, les solutions qui satisfont a²+b²=c² sont de la forme, si 2i+1 est un diviseur de N:
(N²/(2i+1)-1)/2-i.
Là encore, on ne peut trouver de carrés parfaits.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Aoû 2008, 16:54
par Imod » 17 Aoû 2008, 16:54
Et que pensez-vous du triangle rectangle de côtés 7 , 24 et 25 ????
Imod
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 16:58
par magnolia86 » 17 Aoû 2008, 16:58
Imod a écrit:Et que pensez-vous du triangle rectangle de côtés 7 , 24 et 25 ????
Imod
il est rectangle, et son aire est .. 84
-
IPCST
- Membre Naturel
- Messages: 12
- Enregistré le: 17 Aoû 2008, 16:54
-
 par IPCST » 17 Aoû 2008, 17:23
par IPCST » 17 Aoû 2008, 17:23
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Aoû 2008, 17:29
par Imod » 17 Aoû 2008, 17:29
Tiens oui , ça m'apprendra à suivre plusieurs sujets à la fois :marteau:
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
n'implique pas
...
n'est pas premier, par exemple), j'ajoute