Equation fonctionnelle
Olympiades mathématiques, énigmes et défis
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 22 Déc 2008, 23:03
par lapras » 22 Déc 2008, 23:03
Parfait ! Bravo ! :zen:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 24 Déc 2008, 01:13
par kazeriahm » 24 Déc 2008, 01:13
et ben il y a du sacré niveau par ici !!
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Déc 2008, 20:42
par lapras » 24 Déc 2008, 20:42
Equation plutot facile :
Trouver toutes les
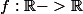
telles que pour tout réels x,y,z et t :
+f(y))(f(z)+f(t))=f(xz+yt)+f(yz-xt))
Lapras :we:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 25 Déc 2008, 13:16
par lapras » 25 Déc 2008, 13:16
Une autre plutôt sympa :
Trouver toutes les
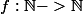
telles que :
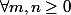
,
)=f(f(m))+f(n))
J'ai du utiliser une petite astuce...
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 25 Déc 2008, 21:20
par ffpower » 25 Déc 2008, 21:20
kazeriahm a écrit:et ben il y a du sacré niveau par ici !!
Merci du compliment mdr :zen:
lapras a écrit:Une autre plutôt sympa :
Trouver toutes les
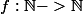
telles que :
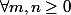
,
)=f(f(m))+f(n))
J'ai du utiliser une petite astuce...
Si je ne me trompe pas,ya des solutions non triviales: par exemple en posant f(n)=n si n est pair,f(n)=n-1 si n est impair
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 25 Déc 2008, 21:50
par lapras » 25 Déc 2008, 21:50
Effectivement et y'en a même beaucoup :we:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 25 Déc 2008, 23:02
par ffpower » 25 Déc 2008, 23:02
lapras a écrit:Effectivement et y'en a même beaucoup :we:
Ca reste quand meme dénombrable :we:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 25 Déc 2008, 23:09
par lapras » 25 Déc 2008, 23:09
Largement ! :)
(sinon je l'aurais indiqué ;))
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 26 Déc 2008, 00:15
par ffpower » 26 Déc 2008, 00:15
Trouver les f continue de R dans R tel que
f(x+y+xy)=f(x)+f(y)+xf(y)+yf(x)
(je sais pas si on peut se passer de f continue ou pas...)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 26 Déc 2008, 02:39
par ffpower » 26 Déc 2008, 02:39
Trouver toutes les f de R dans R telles que pour tout x,y
f(x+y)+f(xy)=f(x)+f(y)+f(x)f(y)
(pas de continuité supposée bien sur^^)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 26 Déc 2008, 11:32
par ThSQ » 26 Déc 2008, 11:32
lapras a écrit:Une autre plutôt sympa :
Trouver toutes les
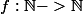
telles que :
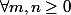
,
)=f(f(m))+f(n))
J'ai du utiliser une petite astuce...
Je peux jouer aussi ? :happy2:
f=0 est sol, on vire cette sol. après.
m=n=0 : f(0) =f(f(0)) = 0 et f(f(n)) = f(n)
f(n) est donc un point fixe de f pour tout n.
soit p = le plus petit entier qui n'est pas un point fixe de f (> 0 donc).
n = qp+r, un autre point fixe, avec r < p, on remplace : f(r) = r donc r=0
Les points fixes (donc tous les f(n)) sont des multiples de p.
...
Les sol sont donc f(qp+r) = (q+g(r))*p avec g(r) une fonction arbitraire de 0..p-1 dans N
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Déc 2008, 11:41
par lapras » 26 Déc 2008, 11:41
Parfait,
Stucieux ;)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Déc 2008, 11:53
par lapras » 26 Déc 2008, 11:53
ffpower > Je l'ai avec f continue ou f monotone.
Mais apres sans continuité j'ai pas vraiment cherché. (je pense qu'il faut obtenit la croissance de f)
sinon, sur les rationnels : f(r)=r ou f est la fonction nulle
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 26 Déc 2008, 16:02
par ffpower » 26 Déc 2008, 16:02
c est deja pas mal.Moi j ai galéré pour montrer que f(1)=0 ou 1
Apres,c ca,faut montrer la croissance de f..
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Déc 2008, 16:22
par lapras » 26 Déc 2008, 16:22
Tu m'étonnes... J'ai du me gouré si t'a galéré pour ca !
Je pose a = f(1)
je calcule avec l'équation fonctionnelle :
f(2)=a^2+a
f(3)=a+a^2+a^3
f(4)=a+a^2+a^3+a^4
mais 4 = 3+1=2+2
donc
f(4)=0.5*(a^4+2a^3+3a^2+2a)
d'où :
2a^4=a^4+a^2
donc a = 0 ou 1 ou -1
de même je calcule de plusieurs manieres différentes
6=4+2=3+3=5+1....
et je met ca en équation, finalement j'arrive à a=0 ou a=1
si a=0 f est fonction nulle
si a=1
par récurrence :
f(x+n)=f(x)+n (n entier, x réel)
apres je montre que si x réel, n entier
f(x*n)=f(x)*n
donc f(q*1/q)=f(1)=1=q*f(1/q)
donc f(1/q)=1/q
f(p*1/q)=p*f(1/q)=p/q
donc pour tout r rationnel f(r)=r
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 26 Déc 2008, 18:53
par ffpower » 26 Déc 2008, 18:53
yep,j ai fait comme ca,sauf pour traiter le cas a=-1..reste la monotonie^^
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Déc 2008, 19:19
par lapras » 26 Déc 2008, 19:19
Tien une autre pour la route (c'est pas vraiment une équation fonctionnelle... mais c'est jolie)
Soit
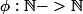
une fonction injective.
Montrer que
}{k^2} > H_n)
avec
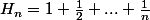
= série harmonique.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 26 Déc 2008, 20:18
par ThSQ » 26 Déc 2008, 20:18
lapras a écrit:Tien une autre pour la route (c'est pas vraiment une équation fonctionnelle... mais c'est jolie)
Soit
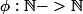
une fonction injective.
Montrer que
}{k^2} > H_n)
avec
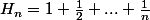
= série harmonique.
Joli en effet mais
ça se fait de manière immédiate par réarrangement (ou Cauchy avec sum_1^n \phi(k) >= n(n+1)/2 mais c'est moins beau je trouve))
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Déc 2008, 20:36
par lapras » 26 Déc 2008, 20:36
Effectivement...
Autre solution qui rejoint quand même le réordonnement...
Soit

telle que la somme soit minimale, pour n fixée.
Supposons qu'il existe
)
alors soit

une fonction telle que :
=\phi(j))
et
=i)
=k)
pour tous les autres k
alors
}{k^2}} - \sum_{k=1}_^n \frac{\psi(k)}{k^2} = \frac{\phi(i)}{i^2}+\frac{\phi(j)}{j^2}-\frac{\phi(j)}{i^2}-\frac{\phi(i)}{j^2}= (\frac{i^2-j^2}{ij})*(\phi(i)-\phi(j)) > 0)
absurde par minimalité
donc
<\phi(2)<...<\phi(n))
donc
\geq k)
d'où le résultat.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Déc 2008, 21:03
par lapras » 26 Déc 2008, 21:03
J'ai peut etre la continuité de f.
pour tout rationnelle r j'ai :
f(x+r)=f(x)+r
en passant à la limite
lim f(x+r) = f(x)
r -> 0
et
lim x+r=x
r->0
Par définition, f continue.
D'où le résultat, f(x)=x.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
telles que :
,
telles que :
,
une fonction injective.
= série harmonique.
