Espace vectoriels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 08 Jan 2008, 17:01
par legeniedesalpages » 08 Jan 2008, 17:01
Bonjour, je ne vois pas comment montrer ce point du cours:
Soient f un endomorphisme d'un K-espace vectoriel E de dimension finie, et v un vecteur de E.
On note
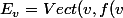,...,f^i(v),...))
sous-espace de E de dimension i.
Alors
,...,f^{i-1}(v)))
est une base de
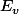
.
Merci pour votre aide.
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 17:11
par klevia » 08 Jan 2008, 17:11
Salut, je dis peut-etre une bétise mais que se passe-t-il si v est un vecteur propre de f ? ça marche pas !!!
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 17:22
par klevia » 08 Jan 2008, 17:22
Soit k tel que {
,...f^{k-1}(v))
} soit libre et {
,...f^{k}(v))
} soit lié
montrons que k=i
alors
)
s'exprime comme combinaison linéaire des vecteurs de {
,...f^{i-1}(v))
} et pour tous n>k
)
aussi.
donc vect {
,...f^{i-1}(v),f^{i}(v),....)
}=vect{
,...f^{k-1}(v))
} et donc k=i.
 par legeniedesalpages » 08 Jan 2008, 17:32
par legeniedesalpages » 08 Jan 2008, 17:32
klevia a écrit:Soit k tel que {
,...f^{k-1}(v))
} soit libre et {
,...f^{k}(v))
} soit lié
montrons que k=i
alors
)
s'exprime comme combinaison linéaire des vecteurs de {
,...f^{i-1}(v))
} et pour tous n>k
)
aussi.
donc vect {
,...f^{i-1}(v),f^{i}(v),....)
}=vect{
,...f^{k-1}(v))
} et donc k=i.
Je ne comprends pas pourquoi
)
s'exprime comme combinaison linéaire des vecteurs de {
,...f^{i-1}(v))
}.
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 17:39
par klevia » 08 Jan 2008, 17:39
dsl, j'ai fait une petite erreur ... je reprends...
)
s'exprime comme combinaison lineaire des vecteurs {
,...f^{k-1}(v))
} et pour tout n>k
)
aussi
d'ou {
,...f^{k-1}(v))
} est une base de Ev ( libre et générateur) et donc k=i
 par legeniedesalpages » 08 Jan 2008, 17:51
par legeniedesalpages » 08 Jan 2008, 17:51
klevia a écrit:dsl, j'ai fait une petite erreur ... je reprends...
)
s'exprime comme combinaison lineaire des vecteurs {
,...f^{k-1}(v))
} et pour tout n>k
)
aussi
d'ou {
,...f^{k-1}(v))
} est une base de Ev ( libre et générateur) et donc k=i
merci klevia, juste encore un petit point qui me chiffonne, pourquoi on a:
pour tout n>k
)
est combinaison linéaire des vecteurs {
,...f^{k-1}(v))
}
et pourquoi on aurait pas par exemple
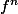
combinaison linéaire de
,f^{k+1}(v))
(je ne vois pas d'où vient le fait que
)
combinaison linéaire des vecteurs {
,...f^{k-1}(v))
} entraîne que cette famille de trois vecteurs
,f^{k+1}(v))
n'est pas libre ?
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 18:15
par klevia » 08 Jan 2008, 18:15
on a donc que
)
s'exprime comme combinaison linéaire des {
,...f^{k-1}(v))
}
c'est a dire que il exite a0,...., ak-1 appartenant à K tel que
=\sum_{j=0}^{k-1}aj.f^j(u))
Ainsi
=f(\sum_{j=0}^{k-1}aj.f^j(u))=\sum_{j=0}^{k-1}a_{j}.f^{j+1}(u)=\sum_{j=0}^{k-2}aj.f^{j+1}(u)+f^k(u))
et
)
s'exprime aussi comme combinaison linéaires des vecteurs {
,...f^{k-1}(v))
}
Au final,
)
est combinaison linéaire des vecteurs {
,...f^{k-1}(v))
}
par récurrence simple pour tout n>k
)
est combinaison linéaire de {
,...f^{k-1}(v))
}
 par legeniedesalpages » 08 Jan 2008, 20:25
par legeniedesalpages » 08 Jan 2008, 20:25
Si je considère la matrice
)
que je sais que son polynôme caractéristique est
(X-2)(X-3))
, et donc que je sais qu'elle est diagonalisable, comment je peux la mettre sous forme diagonale?
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 20:30
par klevia » 08 Jan 2008, 20:30
Ca fait longtemps que je l'ai plus fait mais:
Les valeurs propres de ta matrice sont 1,2 et 3
il faut chercher les vecteurs propres v1,v2 et v3 associés à chacune de ses valeurs.
dans la base (v1,v2,v3)
ta matrice est la suivante:
1 0 0
0 2 0
0 0 3
il peut être utili de connaitre la matrice de passage qui permet de te faire passer de la base canonique à (v1,v2,v3), c'est tout simplement , en colonne, les coordonnées de v1,v2 et v3 dans la base canonique
 par legeniedesalpages » 08 Jan 2008, 20:37
par legeniedesalpages » 08 Jan 2008, 20:37
il faut chercher les vecteurs propres v1,v2 et v3 associés à chacune de ses valeurs.
Justement c'est ce point que je comprends pas vraiment,
Par exemple le sous-espace propre à la valeur 1 :
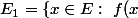-x=0\})
.
Je trouve que
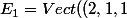))
. Alors je peux déduire que
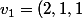)
où j'ai raté un épisode?
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 20:39
par klevia » 08 Jan 2008, 20:39
J'ai pas vérifié tes calcul mais oui, c'est ça !!!
 par legeniedesalpages » 08 Jan 2008, 20:41
par legeniedesalpages » 08 Jan 2008, 20:41
ok et donc après j'aurai
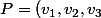)
et alors
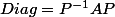
c'est bien ça?
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 20:46
par klevia » 08 Jan 2008, 20:46
cela me semble bon ...
 par legeniedesalpages » 08 Jan 2008, 21:11
par legeniedesalpages » 08 Jan 2008, 21:11
ok merci klevia,
et si je veux calculer
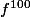
,
donc je considère la matrice

de

par rapport à
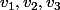
.
Mais est-ce que je peux exprimer facilement
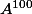
?
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 21:16
par klevia » 08 Jan 2008, 21:16
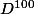
est facile à calculer ...
de plus
^{100}=P^{-1}A^{100}P)
d'ou
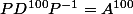
 par legeniedesalpages » 08 Jan 2008, 21:17
par legeniedesalpages » 08 Jan 2008, 21:17
legeniedesalpages a écrit:ok merci klevia,
et si je veux calculer
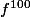
,
donc je considère la matrice

de

par rapport à
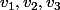
.
Mais est-ce que je peux exprimer facilement
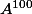
?
que je suis bête, on a
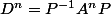
vu que
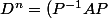^n = P^{-1}A P P^{-1}A P P^{-1}A P.... P^{-1}A PP^{-1}A P)
(n fois)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 08 Jan 2008, 21:19
par tize » 08 Jan 2008, 21:19
Bonjour Klevia,
Salut Legénie, je crois bien que tu es le seul membre du forum à poser une question et y répondre tout en te citant :ptdr:
-
Monyladouce
- Messages: 2
- Enregistré le: 05 Jan 2008, 16:19
-
 par Monyladouce » 08 Jan 2008, 21:31
par Monyladouce » 08 Jan 2008, 21:31
Slt à Vs!
Ben! à peine que j'ai découver ce Forum que je trouve génial, en fait j'éspére étre la Bienvenue :lol:
Apparament;j'ai Besoin d'un cours Bien détaillé avec des exos (Si C possible) de la Mécanique pr Smi/Sma.
et merci D'avance!!!
 par legeniedesalpages » 08 Jan 2008, 21:33
par legeniedesalpages » 08 Jan 2008, 21:33
tize a écrit:Bonjour Klevia,
Salut Legénie, je crois bien que tu es le seul membre du forum à poser une question et y répondre tout en te citant :ptdr:
C'est vrai, c'est impulsif lol
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
} soit libre et {
} soit lié
s'exprime comme combinaison linéaire des vecteurs de {
} et pour tous n>k
aussi.
}=vect{
} et donc k=i.
s'exprime comme combinaison lineaire des vecteurs {
} et pour tout n>k
aussi
} est une base de Ev ( libre et générateur) et donc k=i