Réprésentation d'ensemble (espace vectoriels)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2012, 08:21
par Dante0 » 09 Oct 2012, 08:21
Bonjour,
On me demande de représenter graphiquement les ensembles suivants :



Y, 0\leq \lambda \leq 1<br />\end{array}})
Autant vous dire que je n'ai pas du tout compris la question ni le raisonnement effectué en classe que voici pour A :
A est une sous partie non vide de R
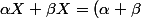X \in A)

Soit
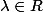

 = (\lambda \alpha)X \in A)
Je comprends pas ce qu'on a essayé de démontrer ici, j'ai l'impression qu'on montre que A est stable pour l'homothétie non ? Auquel cas, je comprends pas du tout ce qu'une "représentation graphique vient faire la... :hum: "
Et je ne sais pas ce qu'est une sous partie non vide...Merci d'avance !
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 09 Oct 2012, 09:50
par Manny06 » 09 Oct 2012, 09:50
Dante0 a écrit:Bonjour,
On me demande de représenter graphiquement les ensembles suivants :



Y, 0\leq \lambda \leq 1<br />\end{array}})
Autant vous dire que je n'ai pas du tout compris la question ni le raisonnement effectué en classe que voici pour A :
A est une sous partie non vide de R
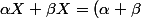X \in A)

Soit
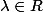

 = (\lambda \alpha)X \in A)
Je comprends pas ce qu'on a essayé de démontrer ici, j'ai l'impression qu'on montre que A est stable pour l'homothétie non ? Auquel cas, je comprends pas du tout ce qu'une "représentation graphique vient faire la... :hum: "
Et je ne sais pas ce qu'est une sous partie non vide...Merci d'avance !
a quoi appartient X ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2012, 11:23
par Dante0 » 09 Oct 2012, 11:23
Manny06 a écrit:a quoi appartient X ?
A un espace vectoriel E quelconque.
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 09 Oct 2012, 12:37
par Manny06 » 09 Oct 2012, 12:37
Dante0 a écrit:A un espace vectoriel E quelconque.
ta définition ressemble à celle d'un sous espace vectoriel
Soit E un espace vectoriel sur R et A une partie de E
A est un sous espace vectoriel de E si et seulement si
A est non vide
A est stable pour l'addition et le produit par un réel
ce qui signifie que A muni de la loi interne addition et de la loi externe produit par un réel a lieu même une structure d'espace vectoriel sur R
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 09 Oct 2012, 12:39
par Manny06 » 09 Oct 2012, 12:39
Manny06 a écrit:ta définition ressemble à celle d'un sous espace vectoriel
Soit E un espace vectoriel sur R et A une partie de E
A est un sous espace vectoriel de E si et seulement si
A est non vide
A est stable pour l'addition et le produit par un réel
ce qui signifie que A muni de la loi interne addition et de la loi externe produit par un réel a lieu même une structure d'espace vectoriel sur R
pour la representation graphique
si X différent du vecteur nul ,{aX,aR} est un droite vectorielle de base X
si X et Y ne sont pas liés {aX+bY} est un plan vectoriel de base (X,Y)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2012, 16:33
par Dante0 » 09 Oct 2012, 16:33
Manny06 a écrit:pour la representation graphique
si X différent du vecteur nul ,{aX,aR} est un droite vectorielle de base X
si X et Y ne sont pas liés {aX+bY} est un plan vectoriel de base (X,Y)
Ca veut dire quoi non vide ? qu'il admet forcément une solution (au moins) ?
Si c'est comme ca qu'il faut répondre qu'est-ce qu'on a fait en classe (démonstration que j'ai mise au premier post) ? :mur: :ptdr:
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 09 Oct 2012, 16:58
par Manny06 » 09 Oct 2012, 16:58
Dante0 a écrit:Ca veut dire quoi non vide ? qu'il admet forcément une solution (au moins) ?
Si c'est comme ca qu'il faut répondre qu'est-ce qu'on a fait en classe (démonstration que j'ai mise au premier post) ? :mur: :ptdr:
une sous partie non vide contient au moins un élément (en principe le vecteur nul)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Oct 2012, 17:03
par Dante0 » 09 Oct 2012, 17:03
Manny06 a écrit:une sous partie non vide contient au moins un élément (en principe le vecteur nul)
Mais pourquoi
sous partie justement ?
Vu ta définition d'un sous espace vectoriel on peut dire que tout les espaces vectoriels qui admettent une loi de composition interne et externe et qui sont non vide sont des sous espaces vectoriels ?
Je pensais qu'un ev etait un ev si justement il admettait une lci et une lce... ce qui reviens à dire que tout les espaces vectoriels sont des sous espaces vectoriels non ?
En clair je comprends pas la différence entre espace vectoriels et sous espace vectoriel.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 10 Oct 2012, 06:02
par Dante0 » 10 Oct 2012, 06:02
up :help: :help:
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 10 Oct 2012, 07:56
par Manny06 » 10 Oct 2012, 07:56
Dante0 a écrit:up :help: :help:
un sous espace vectoriel est effectivement une partie d'un espace vectoriel ayant lui même une structure d'espace vectoriel
si tu veux plus de renseignement,tape "sous espaces vectoriels" sur ton moteur de recherche et va lire l'article sur wikipedia qui est très complet
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2012, 12:18
par Nightmare » 10 Oct 2012, 12:18
Attention, quand on parle de sous-structure, cela ne veut pas généralement pas seulement dire "sous-partie + structure", il faut aussi partager des propriétés avec la grosse partie, comme par exemple avoir le même vecteur nul pour un sev.
Autrement dit une sous-partie d'un ev qui est elle-même un ev n'est pas nécessairement un sev.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 10 Oct 2012, 17:37
par Dante0 » 10 Oct 2012, 17:37
Mais en fait les conditions pour qu'un espace vectoriel en soit un sont les mêmes que pour les sous espaces vectoriels a savoir stable pour la somme vectorielle et pour l'homothétie.. donc je vois pas de différence entre sous espace vectoriels et espace vectoriels... :hum:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2012, 18:55
par Nightmare » 10 Oct 2012, 18:55
Une sous-structure c'est toujours une structure, mais le fait qu'on l'appelle "sous-structure" est pour préciser qu'on se place dans un ensemble structuré plus gros et qu'ils partagent la même structure.
Un sous-espace vectoriel sera toujours un espace vectoriel en tant que tel, mais si on l'appelle sous-espace vectoriel, c'est pour préciser qu'on ne le regarde pas en tant qu'espace ambiant mais plongé dans un espace vectoriel plus gros. Aussi, et comme je l'ai dit plus haut, lorsqu'on dit sous-espace vectoriel, on sous-entend que cette sous-partie, en plus d'être un espace vectoriel à part entière, partage des propriétés identiques avec l'espace vectoriel ambiant, en particulier, ils ont les même opérations et le même vecteur nul.
Ceci se généralise à toutes les structures : Un sous-groupe d'un groupe G, c'est lui même un groupe mais qui est muni des même opérations et du même neutre que G.
Il est tout à fait possible de trouver dans un groupe G une sous-partie qui est un groupe mais qui n'est pas un sous-groupe de G.
Par exemple si je prends G=(Z,+), alors la sous-partie {-1;1} est un groupe pour la multiplication mais n'est pas un sous-groupe de G (car ce ne sont pas le mêmes opérations).
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 10 Oct 2012, 19:40
par Dante0 » 10 Oct 2012, 19:40
C'est quoi G =(Z,+) ?
Sinon pourquoi on a corrigé en classe l'exercice de cette manière si on demandait une représentation graphique ? J'ai pas trop compris ce que mon prof a fait (je sais j'aurais du lui demander :mur: )
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Oct 2012, 20:49
par Dante0 » 11 Oct 2012, 20:49
Up j'aimerais bien comprendre le raisonnement de mon prof...
La semaine pro c'est DS :/
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 12 Oct 2012, 10:15
par Dante0 » 12 Oct 2012, 10:15
Re up :cry:
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 12 Oct 2012, 10:35
par Manny06 » 12 Oct 2012, 10:35
Dante0 a écrit:Re up

je ne comprends pas ce que tu cherches et tu ecris des choses contradictoires
au début tu ecris que A est une sous partie non vide de R
ensuite pour répondre à ma question tu dis que X appartient à un espace vectoriel quelconque que je noterai E
dans ce cas aX avec aR appartient à E donc A est inclus dans E
tout cela n'est pas très precis
ou bien a,b X,Y sont dans R dans ce cas on cherche à démontrer que A est un SEV de R
ou bien a et b sont dans R et X et Y dans E et on cherche à voir si les sous ensembles donnés au debut sont des SEV de E
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 12 Oct 2012, 10:57
par Dante0 » 12 Oct 2012, 10:57
Manny06 a écrit:je ne comprends pas ce que tu cherches et tu ecris des choses contradictoires
au début tu ecris que A est une sous partie non vide de R
ensuite pour répondre à ma question tu dis que X appartient à un espace vectoriel quelconque que je noterai E
dans ce cas aX avec aR appartient à E donc A est inclus dans E
tout cela n'est pas très precis
ou bien a,b X,Y sont dans R dans ce cas on cherche à démontrer que A est un SEV de R
ou bien a et b sont dans R et X et Y dans E et on cherche à voir si les sous ensembles donnés au debut sont des SEV de E
Bienvenue à la fac... :zen:
Y'a marqué représentation graphique, donc je comprends pas pourquoi mon "prof" à commencé à faire des calculs bidons pour démontrer je ne sais quoi... J'ai envie de comprendre ce qu'il a fait/ce qu'il a voulu faire en fait.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Oct 2012, 12:40
par Nightmare » 12 Oct 2012, 12:40
Nous n'avons pas toute la correction donc il est difficile de savoir où ton prof voulait en venir.
Ce que l'on peut en revanche dire c'est que lorsqu'on veut se représenter un objet, en connaitre la nature est un bon départ. En l'occurrence, savoir qu'un ensemble est un espace vectoriel est très utile car on connait bien la forme des espaces vectoriels (des droites, des plans, des espaces...)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 12 Oct 2012, 15:03
par Dante0 » 12 Oct 2012, 15:03
On a pas étudié la formes des ev justement... :doh:
Voila la suite de la correction :
Pour B :
B sous partie non vide de

Soit

 + (\alpha_1 X + \beta_1 Y))
X +(\beta + \beta_1)Y)
Soit
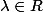
 = (\lambda \alpha)X -(\lambda \beta)Y \in B)
Pour C :
C sous partie non vide de

Soit


 + (\alpha_1 X + \beta_1 Y))
X +(\beta + \beta_1)Y)

C est stable pour la somme
Soit
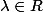
tq
 = \lambda \alpha X + \lambda \beta Y)
=> n'appartient pas forcément à C, l'ensemble C n'est pas stable pour l'homothétie.
:marteau: :marteau: :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
