bonsoir est ce que je pourais avoir de l'aide sur cet exercice?
soit (a,b)∈Z². On pose I=aZ +bZ={s∈I/∃(x,y)∈Z²,s=ax+by}
1)montrer que I est un idéal de Z.
2)I contient donc un plus petit élément positif d tel que I=dZ
a)montrer que d est un diviseur commun à a et b
b)montrer que pour tout c∈Z c|a et c|b =>c|d
c)conclure
Arithmetique
7 messages
- Page 1 sur 1
Re: arithmetique
Aide-toi, et le ciel (bon, plutôt les intervenants habituels) t'aidera.
En particulier, la première question consiste juste à appliquer la définition d'idéal.
En particulier, la première question consiste juste à appliquer la définition d'idéal.
Re: arithmetique
Haha
Oui j'ai fais la première question ce n'etai pas diable
Je suis bloqué a la deuxième
Oui j'ai fais la première question ce n'etai pas diable
Je suis bloqué a la deuxième
Re: arithmetique
Salut,
2a)montrer que d est un diviseur commun à a et b.
On a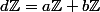
Donc il existe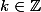 tel que
tel que 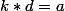
C'est à dire que a est un multiple de d.
C'est à dire que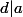 .
.
Tu peux faire de même pour b.
Et d est un diviseur commun à a et b.
2a)montrer que d est un diviseur commun à a et b.
On a
Donc il existe
C'est à dire que a est un multiple de d.
C'est à dire que
Tu peux faire de même pour b.
Et d est un diviseur commun à a et b.
Modifié en dernier par Aispor le 22 Mai 2019, 23:02, modifié 1 fois.
Re: arithmetique
2b). Supposons que c∈Z avec 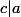 et
et 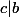
Montrons que c|d
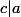 , notons le
, notons le 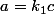
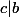 , notons le
, notons le 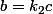
Puisque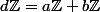
Il existe tel que
tel que 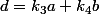
Donc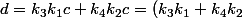c)
d est un multiple de c.
ie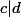
Montrons que c|d
Puisque
Il existe
Donc
d est un multiple de c.
ie
Re: arithmetique
En conclusion.
On a montré que d est un diviseur commun à a et b.
Que si on prend un autre diviseur commun à a et b, alors il divise aussi d. (et donc c est un multiple de d, donc il est en valeur absolue plus petit que d)
Donc d est le plus grand de ces diviseurs communs à a et b.
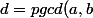)
On a montré que d est un diviseur commun à a et b.
Que si on prend un autre diviseur commun à a et b, alors il divise aussi d. (et donc c est un multiple de d, donc il est en valeur absolue plus petit que d)
Donc d est le plus grand de ces diviseurs communs à a et b.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
