[Arithmetique] Démontrer le Théorème de Bezout
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Delroth
- Messages: 9
- Enregistré le: 16 Jan 2009, 23:17
-
 par Delroth » 17 Jan 2009, 03:39
par Delroth » 17 Jan 2009, 03:39
Bonjour !
Peut-être vous l'aurez remarqué, je suis sur l'arithmétique en ce moment !

Montrer le Théorème de Bezout :
a^b=1 Il existe (u, v) appartenant à Z tel que au + bv = 1.
J'ai " " !
Quelqu'un saurait m'aider ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Jan 2009, 07:23
par lapras » 17 Jan 2009, 07:23
Salut
soit on le fait de façon classique avec l'algorithme d'euclide, sinon autre façon :
considère le plus petit m entier strictement positif qui s'écrit sous la forme de au + bv. que peux tu dire sur m ?
-
Delroth
- Messages: 9
- Enregistré le: 16 Jan 2009, 23:17
-
 par Delroth » 17 Jan 2009, 12:08
par Delroth » 17 Jan 2009, 12:08
Par le coefficiant de Bezout :
m = a^b mais justement... Est-ce qu'on a le droit de le montrer comme ça... Jveux dire, démontrer le théorème grâce au coefficient.. ? :hein:
Et comment le montrer par l'algorithme d'euclide ?! :id:
-
AL-kashi23
- Membre Rationnel
- Messages: 765
- Enregistré le: 14 Aoû 2007, 10:59
-
 par AL-kashi23 » 17 Jan 2009, 12:43
par AL-kashi23 » 17 Jan 2009, 12:43
Moi je te propose d'utiliser la définition du pgcd comme somme d'idéaux... Bezout s'en déduit tout de suite et c'est bien moins fastidieux que l'utilisation de l'algo d'euclide.
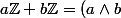\mathbb{Z})
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Jan 2009, 12:56
par lapras » 17 Jan 2009, 12:56
Oui mais les idéaux sont ils vus en prépa ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 13:13
par leon1789 » 17 Jan 2009, 13:13
Dans une démonstration le théorème de Bézout, il est sous-entendu qu'on utilise pas le fait que Z est un anneau principal (cf idéaux and co), sinon ce n'est pas une démo, mais une trivialité !
L'algo d'Euclide étendu aux coefficients de Bézout (justement :id:) fait ce qu'il faut.
-
SimonB
 par SimonB » 17 Jan 2009, 13:18
par SimonB » 17 Jan 2009, 13:18
lapras a écrit:Oui mais les idéaux sont ils vus en prépa ?
C'est au programme de maths spé MP. Je ne sais pas pour les PSI et les PC.
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 17 Jan 2009, 13:19
par guigui51250 » 17 Jan 2009, 13:19
AL-kashi23 a écrit:Moi je te propose d'utiliser la définition du pgcd comme somme d'idéaux... Bezout s'en déduit tout de suite et c'est bien moins fastidieux que l'utilisation de l'algo d'euclide.
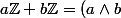\mathbb{Z})
Euh il n'y a pas une autre methode? parce qu'en spé maths (Terminale) on l'a démontré ce théorème mais sans parler des idéaux (inconnu au bataillon)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 17 Jan 2009, 15:10
par _-Gaara-_ » 17 Jan 2009, 15:10
AL-kashi23 a écrit:Moi je te propose d'utiliser la définition du pgcd comme somme d'idéaux... Bezout s'en déduit tout de suite et c'est bien moins fastidieux que l'utilisation de l'algo d'euclide.
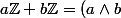\mathbb{Z})
pour faire ça faut revoir tout le chapitre ^_^
-
Delroth
- Messages: 9
- Enregistré le: 16 Jan 2009, 23:17
-
 par Delroth » 17 Jan 2009, 17:43
par Delroth » 17 Jan 2009, 17:43
Ok alors pour ceux que ca interesserait, en fait j'ai retrouvé un moment dans le cours où il expliquait la démonstration, c'est avec le coefficiant qu'on fait ça :)
Merci à tous ! :we: :we:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 17:47
par leon1789 » 17 Jan 2009, 17:47
Delroth a écrit:c'est avec le coefficiant qu'on fait ça

tu veux dire quoi ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Jan 2009, 17:58
par ThSQ » 17 Jan 2009, 17:58
Delroth a écrit:c'est avec le coefficiant qu'on fait ça

Euh, quel coefficient au juste ??
Sinon la démo classique est là :
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Bachet-B%C3%A9zoutPour Léon : trouver un anneau non noethérien dans lequel deux éléments quelconques possèdent un pgcd :happy:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 18:09
par leon1789 » 17 Jan 2009, 18:09
ThSQ a écrit:Pour Léon : trouver un anneau non noethérien dans lequel deux éléments quelconques possèdent un pgcd :happy:
on prend un anneau factoriel non noethérien comme Z[X_1,X_2,....] :happy:
Tu connais les anneaux de valuation ? pgcd(a,b)=a ou b !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Jan 2009, 18:14
par ThSQ » 17 Jan 2009, 18:14
Mince j'avais dit non noethérien justement pour que tu ne sortes pas un anneau de polynômes mais j'avais plus pensé à celui-là :marteau:
Bon, ni noethérien ni factoriel alors :zen:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 18:38
par leon1789 » 17 Jan 2009, 18:38
ThSQ a écrit:Mince j'avais dit non noethérien justement pour que tu ne sortes pas un anneau de polynômes mais j'avais plus pensé à celui-là :marteau:
Bon, ni noethérien ni factoriel alors :zen:
Je peux tricher ?
--> ( ZxZ ) [X_1,X_2,....] (pas intègre, pas factoriel, pas noethérien)
Sérieux, un exemple qui ne soit pas un anneau de polynômes...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 18:59
par leon1789 » 17 Jan 2009, 18:59
ThSQ a écrit:Mince j'avais dit non noethérien justement pour que tu ne sortes pas un anneau de polynômes mais j'avais plus pensé à celui-là :marteau:
Bon, ni noethérien ni factoriel alors :zen:
Je peux tricher ? (pas intègre, pas factoriel, pas noethérien)
--> ( ZxZ ) [X_1,X_2,....]
--> Un produit infini de corps
Tu veux un anneau à pgcd, intègre, non noethérien, non factoriel, qui ne soit pas un anneau de polynôme ? ...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Jan 2009, 19:11
par ThSQ » 17 Jan 2009, 19:11
Zactement !
Sinon un corps n'est-il pas un exemple (certes idiot) d'anneau de valuation ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 19:16
par leon1789 » 17 Jan 2009, 19:16
ThSQ a écrit:Zactement !
bon alors je vais prendre un anneau de valuation dont le groupe des valeurs est R (ou plus simplement Z^2)
ThSQ a écrit:Sinon un corps n'est-il pas un exemple (certes idiot) d'anneau de valuation ?
c'est une question de définition : je crois qu'empêche d'entrée de jeu à un anneau de valuation d'être un corps.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Jan 2009, 22:44
par ThSQ » 17 Jan 2009, 22:44
Je pensai pas à un truc comme ça mais je regarderai demain
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Jan 2009, 23:14
par Imod » 17 Jan 2009, 23:14
Bonsoir,
On s'interroge sur Bézout dans

et on sort des idéaux et autres anneaux factoriels , noethériens ... trouver l'erreur :zen:
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités