[Colle] - Arithmétique, Fibonacci et Lucas

[Lostounet]

Bonjour,

Je dois rédiger mon exercice de colle (infaisable comme d'habitude..). Je n'y arrive pas vraiment:

On définit les nombres de Fibonacci par la relation:




On montre que pour tout m > 1, pour tout n > 0, on a:


1. Soit d dans N, m> 1 et n > 0
Montrer que pour tout , on a:

(d divise et ) (d divise et )

Je sais que je dois faire une récurrence sur l'équivalence mais je n'arrive pas à le rédiger...

2. On suppose en outre que m > n, et on note r le reste de la division euclidienne de m par n. Montrer que:

3. Montrer le théorème de Lucas, qui affirme que:

[Lostounet]

Je viens de trouver la correction de l'exo sur le net ici: http://iml.univ-mrs.fr/~ritzenth/cours/TD_CAPES.pdf

La correction est-elle bien rédigée? :p

[Ben314]

Pour le 1), effectivement, le plus "naturel" (mais il y a d'autres méthodes), c'est de faire une récurrence sur k. L'amorce pour k=1 est immédiate et, pour l'hérédité, tu utilise la formule rappelé en début d'énoncé (et le fait que et sont premiers entre eux)

Sinon, la correction proposée par le site que tu cite (!!!) me semble tout à fait correcte.
Mais ça serait pas con que tu (re)cherche par toi même...

[Mathusalem]

Je viens de trouver la correction de l'exo sur le net ici: http://iml.univ-mrs.fr/~ritzenth/cours/TD_CAPES.pdf

La correction est-elle bien rédigée? :p

Si l'exercice t'a posé problème, tu ne comprendras jamais en lisant une correction rédigée par un autre autant que si tu avais résolu toi-même. La correction passe sous le tapis toutes les questions auxiliaires que tu pourrais te poser (pourquoi ça et pas autre chose, comment ça se fait que ... etc) et qui mènent à une compréhension profonde du/des concepts.

J'ai souvent fait cette erreur, et ça m'a coûté cher au final

[Lostounet]

Salut,

Le problème c'est que si je fais ça à chaque fois, je finis par ne pas avoir assez de temps pour vivre. Je ne sais souvent pas faire les exercices (sauf miracle), je me dis autant regarder la correction...
Je préfère faire un maximum d'exercices, même sans comprendre le concept en profondeur. Car de toute façon je n'aurai pas la moyenne au DS, autant faire un maximum d'exos.

:/ lol

[Skullkid]

Le problème c'est que si je fais ça à chaque fois, je finis par ne pas avoir assez de temps pour vivre. Je ne sais souvent pas faire les exercices (sauf miracle), je me dis autant regarder la correction...
Je préfère faire un maximum d'exercices, même sans comprendre le concept en profondeur. Car de toute façon je n'aurai pas la moyenne au DS, autant faire un maximum d'exos.

Salut, c'est toujours un peu délicat de donner ce genre de conseils quand on n'est plus dans le bain, mais je plussoie Ben314 et Mathusalem, à mon avis ce n'est pas une bonne idée de privilégier quantité à qualité. Il est assez peu probable que tu arrives à mémoriser sur le long terme les solutions de tes exercices. Même si tu y arrives, d'une part ca représente un stress mental assez important, d'autre part tu vas t'emprisonner dans une démarche contre-productive.

Ne te soucie pas de tes notes aux DS (je sais que c'est plus facile à dire qu'à faire après le collège-lycée et la sacralisation des notes qui y est faite). La première chose à faire c'est de comprendre ton cours et d'être capable de refaire toutes les démonstrations et exemples qui y figurent (au moins lister les grandes étapes de chaque preuve et comprendre comment elles s'articulent). C'est seulement une fois que tu es satisfait de ta maîtrise du cours que tu peux attaquer les exercices, et là encore, il vaut mieux bien comprendre un seul exercice que d'être capable de mémoriser la solution de 10 exercices et tout oublier 2 jours après.

Le mois de décembre de sup est généralement assez dur (il fait froid, il fait sombre, on est fatigué après 3 mois intensifs à un rythme nouveau, ...) mais essaye de garder à l'esprit que le but du jeu c'est d'apprendre les choses en profondeur. Courage !

[Lostounet]

Je vais faire de mon mieux ... ! Je vais apprendre à relativiser, et je vais apprendre à apprendre les maths "méchantes". Mais il me faut du temps pour tout cela :)

Pour l'instant, ça a surtout été une épreuve d'adaptation, au nouveau rythme mais aussi à un tas de nouvelles choses. Le choc a été rude mais je vais persévérer.

Tout ira mieux dans 10 jours quand je reverrai ma famille, mes amis que je n'ai pas revus depuis aout :D

[Doraki]

D'abord ton énoncé est faux ou alors tu l'as mal recopié.

1. Soit d dans N, m> 1 et n > 0
Montrer que pour tout k>=1 , on a:
(d divise Fn et Fm) (d divise Fn et F(n+km))

c'est plutôt
(d divise Fn et Fm) (d divise Fm et F(n+km))

[Lostounet]

Dans mon énoncé c'est bien Fn (et même sur le site plus haut). Pourquoi c'est faux?

Question - puis-je montrer par l'absurde sur une récurrence?
Je veux dire que si je suppose qu'il existe un diviseur commun strict d de Fn et Fn+1, alors d divise Fn+2. Par récurrence d divise tous les termes de la suite.

puis je calcule F3=2
F4=3

Comme F3 et F4 n'ont pas de diviseur commun strict.. D ne peut diviser deux termes consécutifs. Sauf que rien ne dit que ça ne devient pas vrai à partir d'un certain rang... Mais ils disent que c'est pour tout n, donc c'est nécessairement faux !

[Ben314]

Je veux dire que si je suppose qu'il existe un diviseur commun strict d de Fn et Fn+1, alors d divise Fn+2. Par récurrence d divise tous les termes de la suite.

Si tu veut démontrer que et sont premier entre eux par l'absurde, ben tu ferait mieux de "descendre" les indices plutôt que de les monter (i.e. montrer que, si d divise et alors il divise et )
Ca te permettrait de conclure à une contradiction... en un temps fini... :lol3: alors qu'en faisant augmenter n, je sais pas où tu vas la trouver ta contradiction...

Sinon, il y a un truc archi classique qui se montre par exemple par récurrence (ou, de façon bien plus simple, avec des matrices si tu sait ce que c'est), c'est que ce qui (c.f. bézout) montre direct que et sont premiers entre eux.

[Lostounet]

Je les ai vu en train de poser des Un = (-1)^n et Vn =(-1)^n
pour trouver des coeff de bezout. En fait j'avais montré lors de ma colle précédente la relation que tu cites, mais vu qu'ils disent qu'on est pas censé avoir vu les suites de Fibonacci...

Donc j'essaye de redescendre jusqu'à 1?
en fait est-il possible de montrer qu'un truc est faux pour tout n, par récurrence? Je ne pense pas


si une propriété est fausse au rang n et que Pn vraie implique Pn+1 vraie, on peut dire que Pn est toujours fausse?

[Ben314]

En fait est-il possible de montrer qu'un truc est faux pour tout n, par récurrence?

Sur le principe "théorique", forcément que oui, vu que montrer qu'un truc est faux, ça veut dire montrer que ça négation est vrai...

Par exemple, ici, tu voudrait montrer que
: "F_n et F_{n+1} ont un diviseur commun autre que "
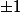
est fausse pour tout n.
Bon, ben ça revient à montrer que la négation est vrai pour tout n.
L'amorce va donc consister à montrer que P(0) est fausse.
Et l'hérédité, ça va consister à montrer que, pour tout n, on a
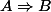
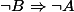
Or, comme une implication affirme exactement la même chose que ça contraposée , ça revien à dire qu'il faut montrer que, pour tout n, on a

Et après tout ce "blablabla" théorique, on retombe sur ce que je te disait au début... c'est à dire que pour montrer qu'un truc est faux, il vaut mieux "descendre" que "monter"...

Là, tu vois, je sens qu'on vient "d'inventer la lune" avec une nouvelle façon de voir le principe de récurrence, c'est à dire que :
- Si une propriété est fausse au rang 0
- Et si, pour tout entier n, on a P(n+1) => P(n)
Alors elle est fausse pour tout n...
balèze non ? :doh:

Si une propriété est fausse au rang n et que Pn vraie implique Pn+1 vraie, on peut dire que Pn est toujours fausse?

Non : c'est [ P(n+1) vraie => P(n) vrai ] qu'il te faut pour conclure.

[Lostounet]

C'est intéressant vu comme ça!
Merci Ben, toujours des réponses qui me redonnent envie de faire des maths !

[Doraki]

Dans mon énoncé c'est bien Fn (et même sur le site plus haut). Pourquoi c'est faux?

Ben par exemple, d=3,m=2,n=4,k=2 donne :

3 divise F4 et 3 divise F2 3 divise F4 et 3 divise F8
3 divise 3 et 3 divise 1 3 divise 3 et 3 divise 21
faux vrai
faux

Je suis vraiment pas allé chercher mon contre-exemple très loin, vu que c'est la 2ème paire possible qui ait un diviseur commun non trivial.

D'ailleurs dans la correction ils montrent
(d divise Fn et Fm) (d divise Fn et F(m+kn)) (qui est vrai mais pas ce que dit l'énoncé)
et pas
(d divise Fn et Fm) (d divise Fn et F(n+km)) (qui est ce que dit l'énoncé mais faux)

[Lostounet]

D'accord, je vais revérifier. C'est bien ce qu'ils démontrent dans la correction en plus !

Donc l'équivalence à démontrer est du coup:

(d divise et ) (d divise et ) ?

Je vais essayer de rédiger ça ici.

Pour le fait que F_n et F_n+1 sont premiers entre eux:

Lemme: Montrons que et sont premiers entre eux. Pour cela, raisonnons par l'absurde. Soit n>=1 dans N.
On suppose que et admettent un diviseur strict u. u divise toute combinaison linéaire de et de, en particulier u divise leur différence.
Or par définition, . Donc ... comment arrive-t-on à 1? proprement, avec une récurrence..
[...]

u divise 1, contradiction. Donc Fn et Fn+1 sont premiers entre eux

[Lostounet]

Je suppose le résultat précédent bien démontré...

Démontrons par récurrence sur k, que pour tout k dans N, tel que k>=1, on a l'équivalence:

(d divise et ) (d divise et ).

Raisonnons par double implication.
Au rang k = 1, montrons que
(d divise et ) => (d divise et ).

Comme d divise , d divise
Comme d divise, d divise

Donc d divise la somme, d divise

Montrons qu'au rang k = 1 :
(d divise et ) => (d divise et )

d divise et donc d divise et d divise , donc d divise

. D'après le lemme, comme d divise, d ne peut diviser, donc d divise Fm (th. de Gauss)... mais je ne comprends pas, d peut valoir 1 et tout diviser..

[Doraki]

(pour ton post de 13h35)

Ben là as tu as montré que "pour tout n, P(n) => P(n-1)" où P(n) = "Fn et F(n+1) ne sont pas premiers entre eux".

Donc soit tu t'embêtes à faire une récurrence à l'envers et de dire (par récurrence sur m) que pour tout m et n, P(n) => P(n-m), puis tu prends m=n-1 et t'en déduis que P(n) => P(1) et là tu es redescendu jusqu'à 1, comme tu dis.

Soit tu réalises que tu as montré l'hérédité de "non P(n)" et tu fais donc une récurrence tout ce qu'il y a de plus normale sur n pour montrer que pour tout n, non P(n).


En résumé il faut TOUJOURS penser en 1er à faire une récurrence ; et ensuite (pour l'hérédité) voir si ça aide de passer par l'absurde.

Et ne pas faire l'inverse (absurde, puis ??? puis récurrence à l'envers ?)

puisque de toutes façons tu es forcé de faire une récurrence quelquepart, autant la faire dès le début.

---

Pour ton autre post, je pense que le mieux c'est d'amorcer à k=0 plutôt qu'à k=1.

Est-ce que tu as fait la question 4 déjà ou pas ?

Ensuite ton énoncé dit bien que cette propriété est vraie dès que l'égalité (*) de la question 4 est vérifiée, donc cette propriété n'a aucun rapport avec l'égalité de la question 3. Donc de base au moment où tu écris que d divise Fm * Fn+1, c'est que tu fais trop compliqué.

[Lostounet]

Je ne comprends pas très bien la deuxième démarche. Je montre l'hérédité de "non P(n)", donc que F_n et F_n+1 SONT premiers entre eux?

Je suppose que F_n et F_n+1 sont premiers entre eux...Et je montre que F_n+1 et F_n+2 sont premiers entre eux.. Je ne vois pas.

----

Je ne peux pas traiter k = 0 car par définition k>= 1 d'après l'énoncé

PS. J'ai l'impression qu'on ne travaille pas sur le même énoncé lol.
Car mon exercice de colle me permet d'utiliser la relation donnée entre Fm et Fn je pense... Sinon je ne sais pas faire autrement.

[Doraki]

Oui tu montres cette implication "par l'absurde" (ou par contraposée, c'est la même chose) et tu refais la même chose que ce que t'avais fait avant avec ton u qui divisait les gens.

[Doraki]

Je ne peux pas traiter k = 0 car par définition k>= 1 d'après l'énoncé

Etant donné que la propriété est trivialement vraie à k=0, le seul moyen où ça pourrait être gênant de commencer à 0 plutôt qu'à 1 est si la preuve de l'hérédité ne marche pas pour le cas k=0 => k=1, ce dont je doute extremement fort.

Et puis sinon oui, j'étais en train de lire le pdf que t'as donné donc oui si ta colle ne parle pas de la question 3 (essentiellement, montrer que pgcd(Fn,Fm) = pgcd(Fn,F(n+m))), je retire ce que j'ai dit.